IEU OpenGWAS project (mrcieu.ac.uk)

UK Biobank - UK Biobank

GWAS Catalog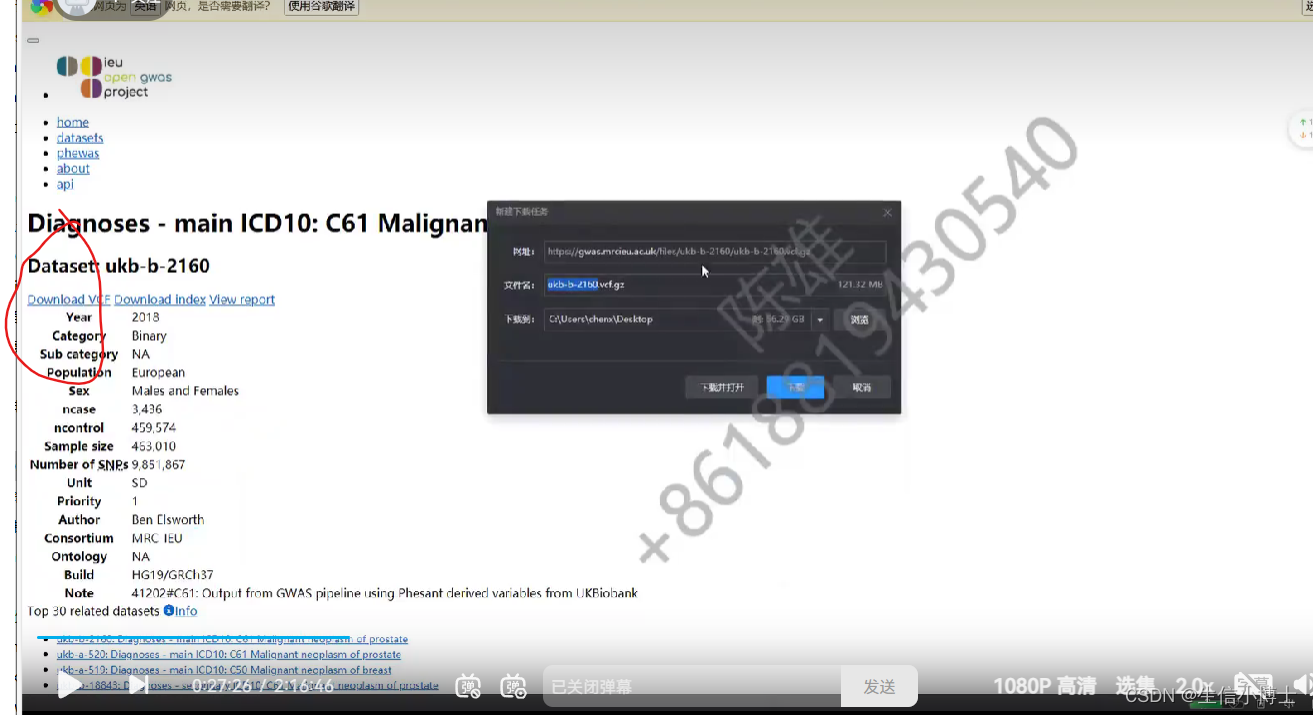 

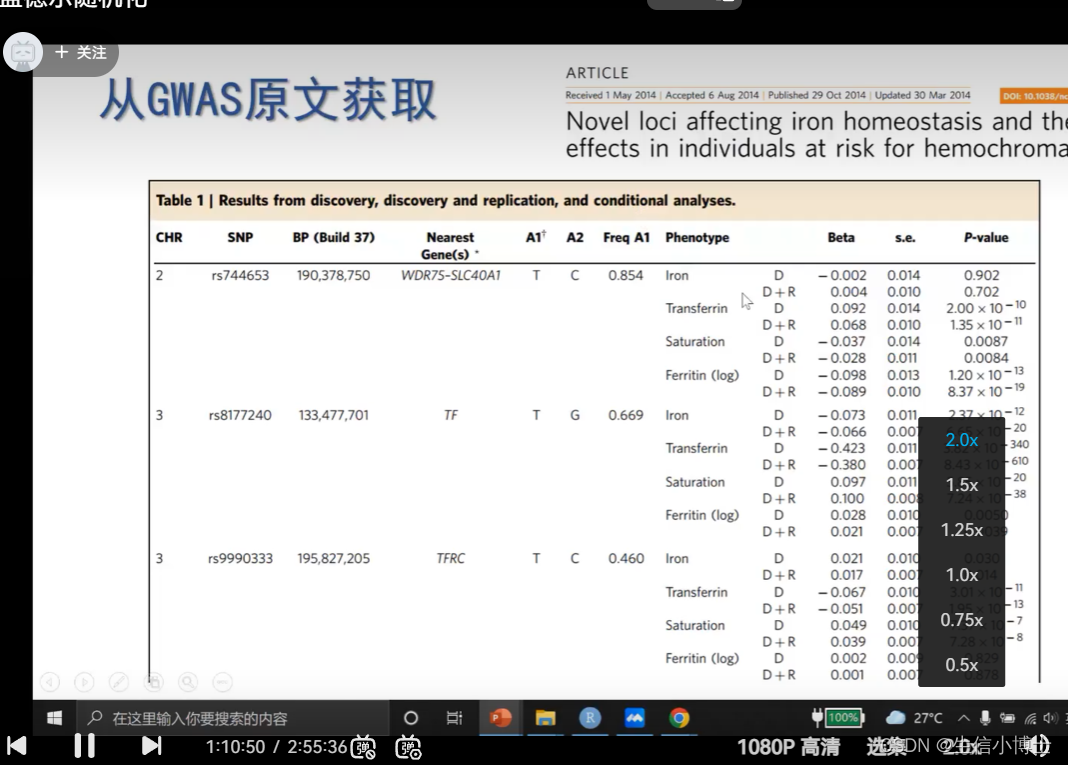
在孟德尔随机化（Mendelian randomization，MR）研究中，对于暴露数据我们只需要那些显著的SNP信息，这样的信息在各种GWAS数据库中都是很容易获取的。但是，关于结局的数据，由于需要SNP和结局不相关，所以很多时候这种不显著的结果无法直接从文章或者数据库中查询到，这时候我们需要下载完整的GWAS summary数据了，这种数据一般包含上百万乃至上千万的SNP信息，所以数据量比较大（压缩后在200M左右），希望大家有所认识，有所准备。

接下来，我将介绍如何从GWAS catalog下载完整的GWAS summary 数据

首先，进入GWAS catalog的官网（https://www.ebi.ac.uk/gwas/），点击Summary statistics（如下图所示）

进入Summary statistics后点击Available studies（如下图所示）

最后，你将进入如下界面（链接：https://www.ebi.ac.uk/gwas/downloads/summary-statistics）

该界面主要由三部分组成

第一块是 “List of published studies with summary statistics“（如下图所示）：这里的GWAS研究都是已经发表的，质量有保证，你可以在检索框（红色标记处）里输入关键词检索感兴趣的表型。

第二块是 “List of prepublished/unpublished studies with summary statistics“（如下图所示）：这里的GWAS研究是未发表见刊的（可能是来源于预印本），质量无法保证，你可以在检索框（红色标记处）里输入关键词检索感兴趣的表型。这里的表型可能会比较新，是对已发表数据的补充。当你实在找不到数据时，不妨来这里试试。

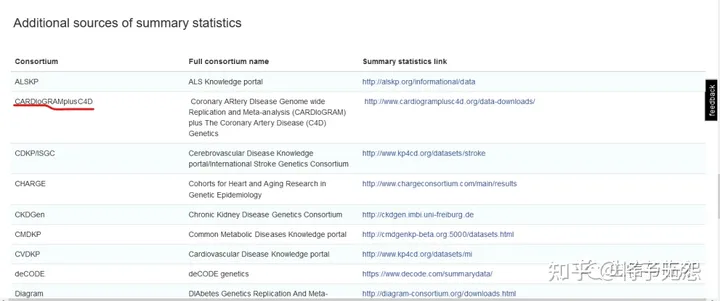
第三块是“Additional sources of summary statistics“（如下图所示）：这里整理汇总了目前GWAS研究协作体（consortium）的相关信息。一般这些协作体会建有自己的网站来存储数据，我们可以到它们的官网上下载完整的GWAS summary 数据。图中用红色标记的是冠心病研究的协作体。

GWAS catalog数据库是一个宝藏，米老鼠在这里抛砖引玉，希望大家能更深入地研究利用它，也欢迎私信交流你的idea（微信：MedGen16）！

PS: GWAS catalog有时候需要开国外代理模式才能使用，小伙伴们提前准备好哈！

ssgac

获取gwas的来源

 

包含的数据

 

1 读取exposure数据

1.2 保存exposureshuju

开始实操

读取暴露数据

读取结局数据

harmonize data 

mr

敏感性分析 

 显著且相互独立，获取工具变量

 优点就是快，缺点就是有可能

可能不相互独立 连锁不平衡

5 * 10 -8

 

说明工具变量与暴露相关   与结局不相关。

可能丢掉了snp

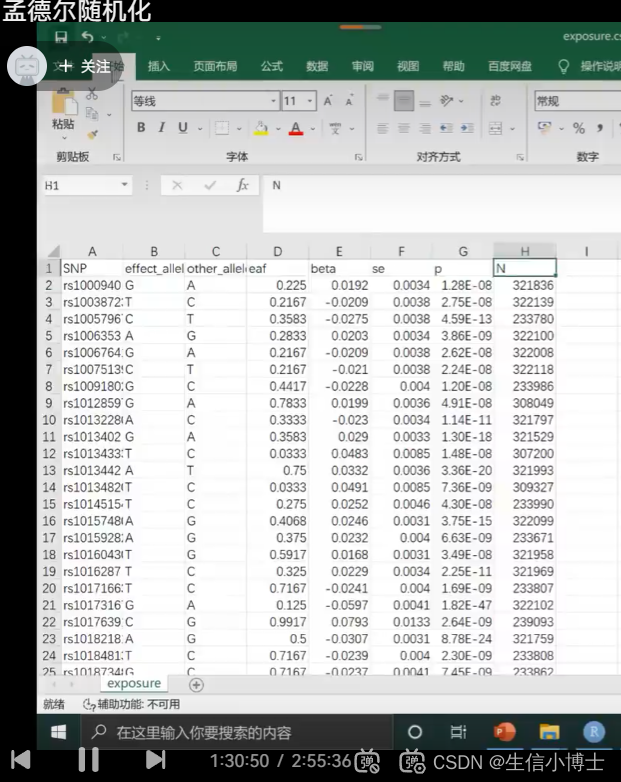
step1 r读取暴露数据

 需要相关性设置 subset函数   5*10 -8

独立性设置     clump函数   去除连锁不平衡   ld r2越小越好，通常0.001 最大0.1.   

取决于snp数     distance 500kb也可以

统计强度设置  f>10较好

 1.1  需要相关性设置 subset函数   5*10 -8

1.2修改文件的列名

1.3 独立性设置 重新读取subset之后的暴露数据read_exposure_data

clump默认  ldr2<0.01

可以之后再clump  clump_data

 step2 读取outcomedata

1 read.table 

2 merge 取交集

2.1 改列名

 

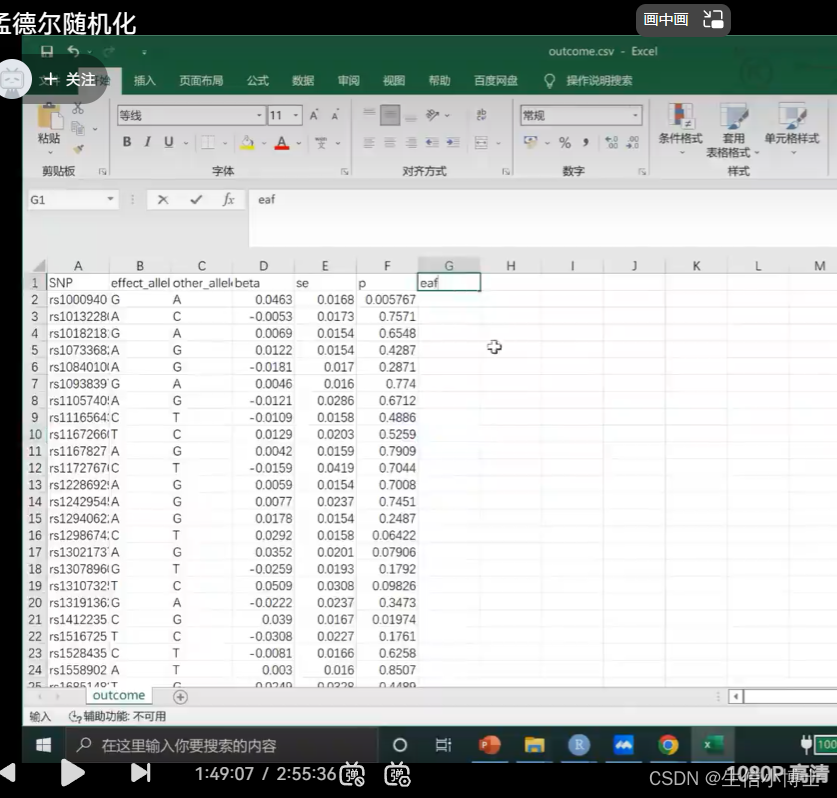
3 read_out_come_data

小结

 效应等位基因

 需要使用代码协调 A--.>T

代理snp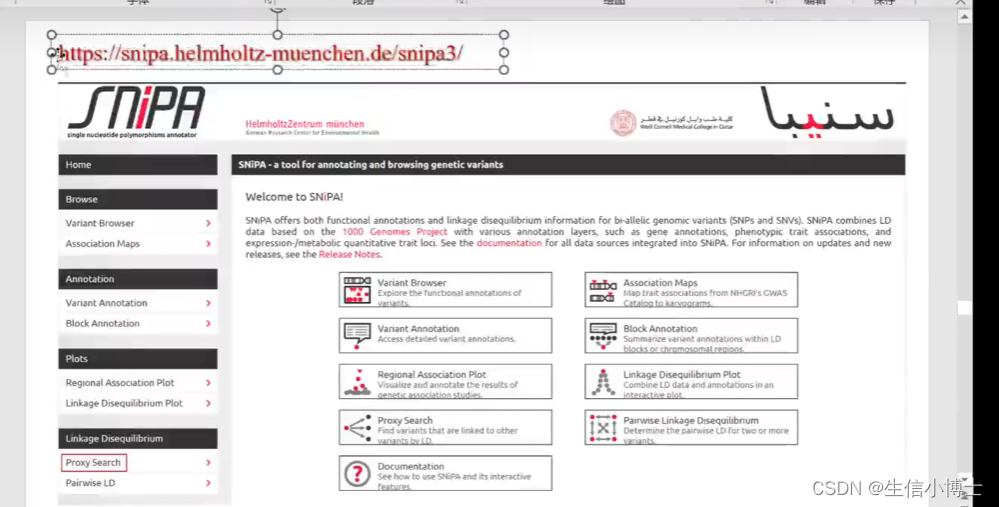

代理snp 设置为0.8  越大越说明他们之间存在连锁不平衡 说明他们之间相互影响大  他们互相替代的可能性就高

但是独立性设置时候要让ld r2尽可能小0.001

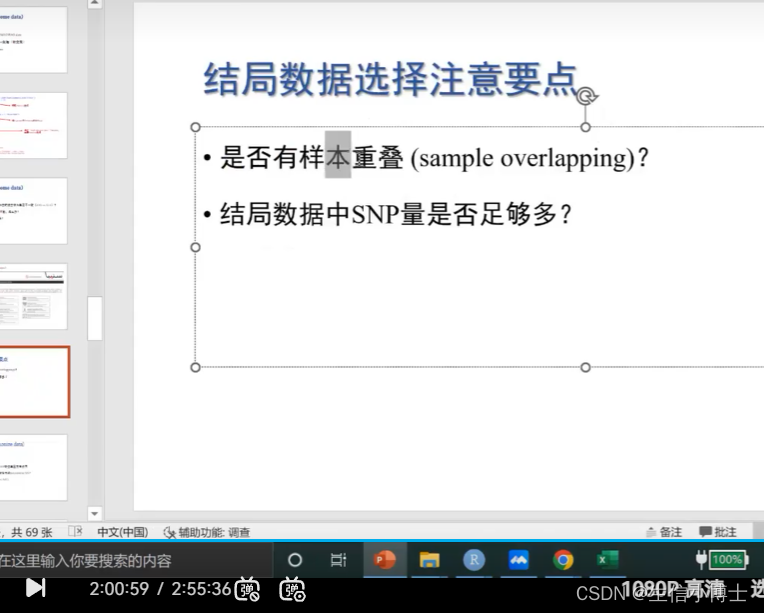
样本重叠了

暴露数据 50w 

结局数据 100w

snp数据必须大于500w才能用  正常可达1000w

step3协调 harmonise

剔除回文序列 

保存文件

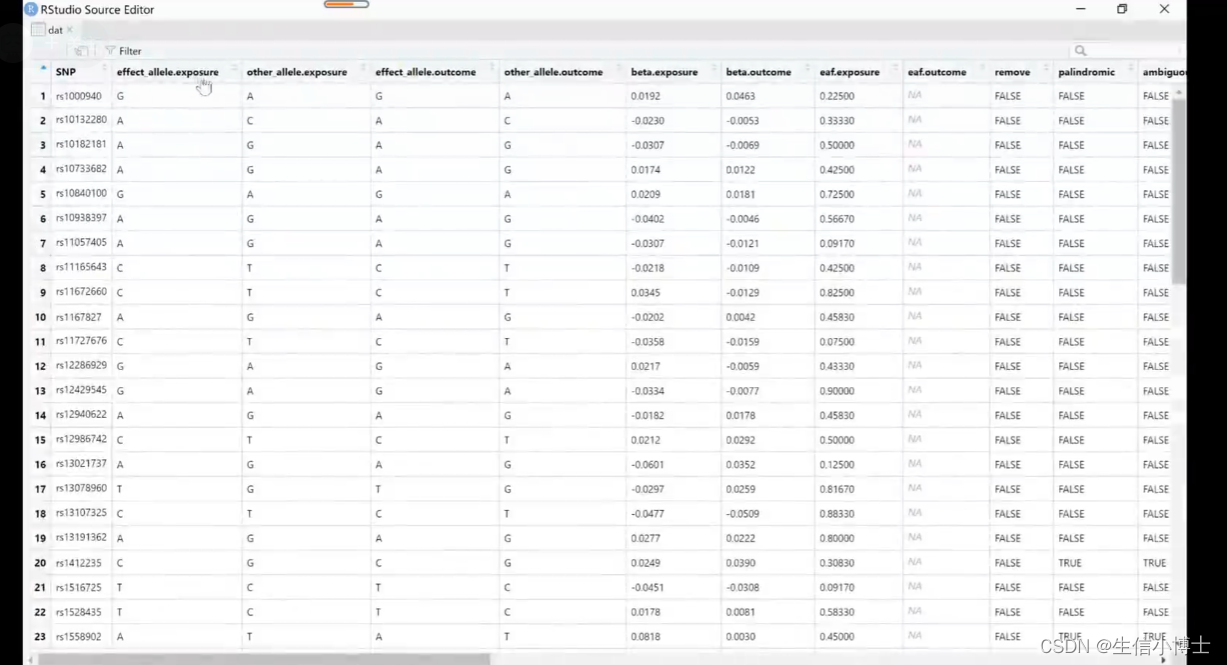
 确保暴露的snp与结局不相关

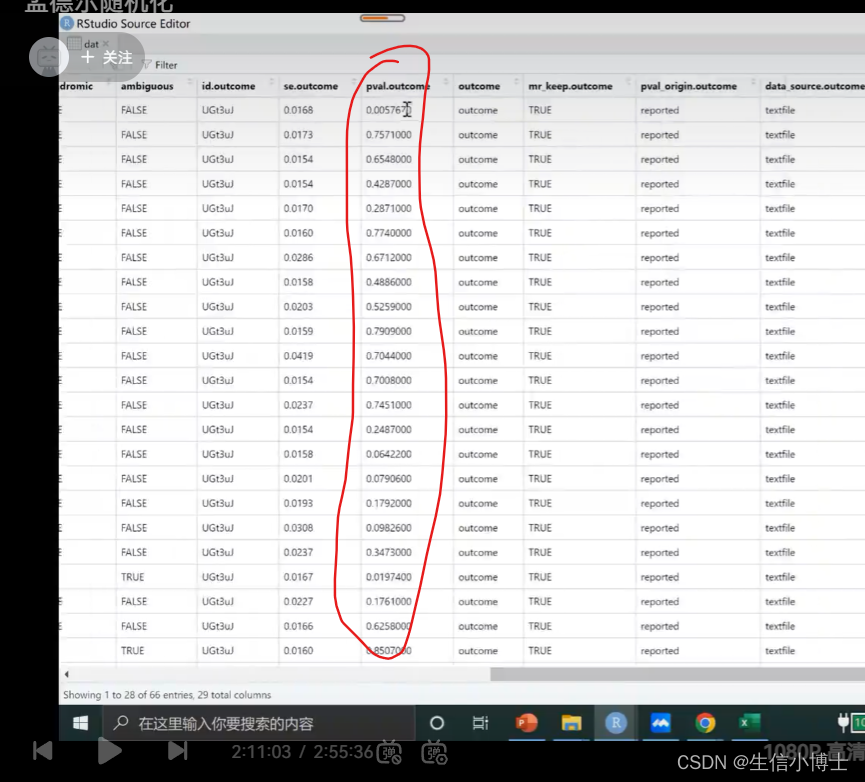
snp与暴露要相关

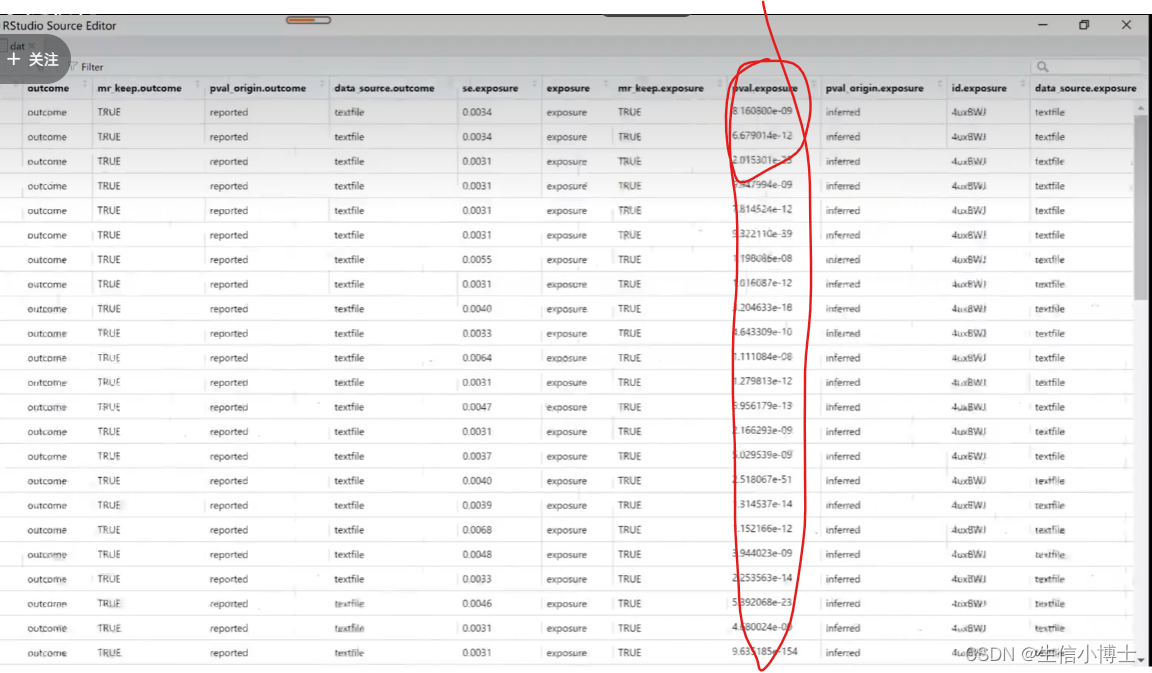
snp与结局不相关  符合假设

 

step4 mr

ivw为随机效应模型

结局为连续变量使用 beta值  以0 为界

结局为分类变量时候 ，需要对数转化，使用or 以1为界

使用其他方法

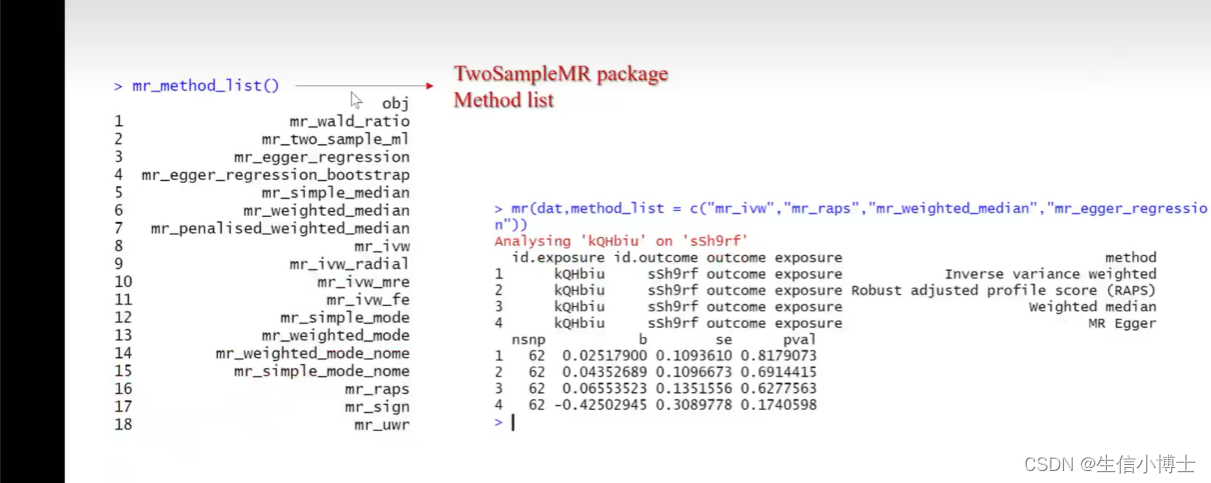
mr（dat,method_list=c()）

 画散点图时，选择想要的方法画图

5 结果可视化

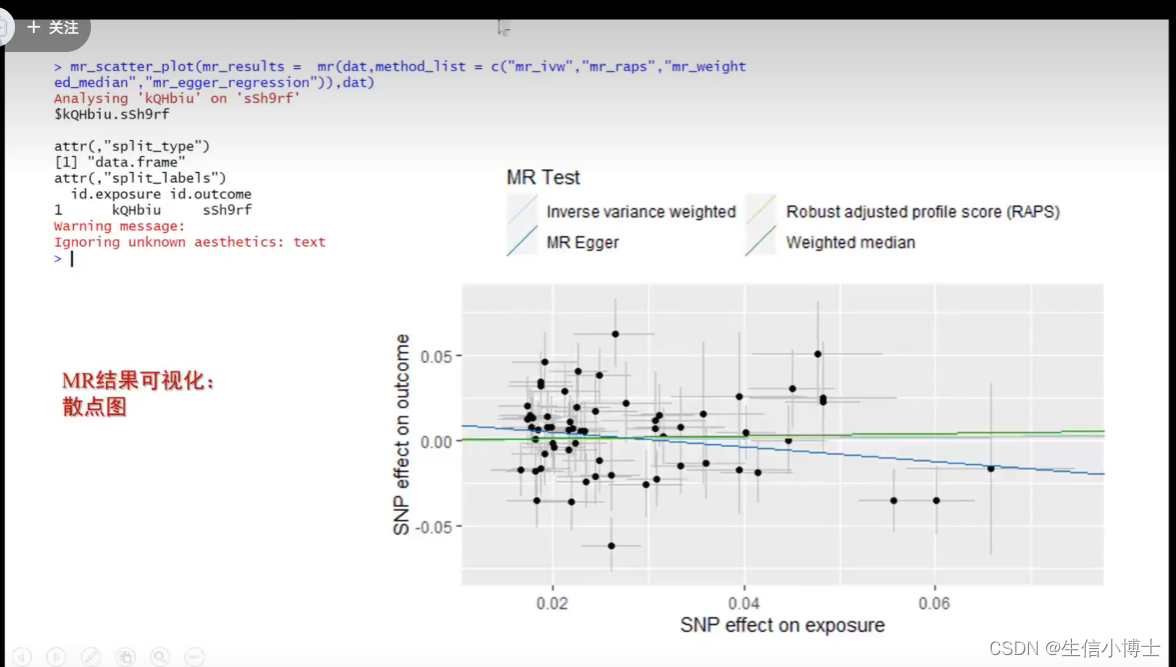
6 敏感性分析包括：异质性检测  多效性检测 

异质性检测

异质性《0.05 则存在异质性，

有异质性，对结果的可靠性不影响

nbdistribution 设置为1w，更准确

6.1 找出对异质性影响最大的snp run_mr_pressor

nb

 

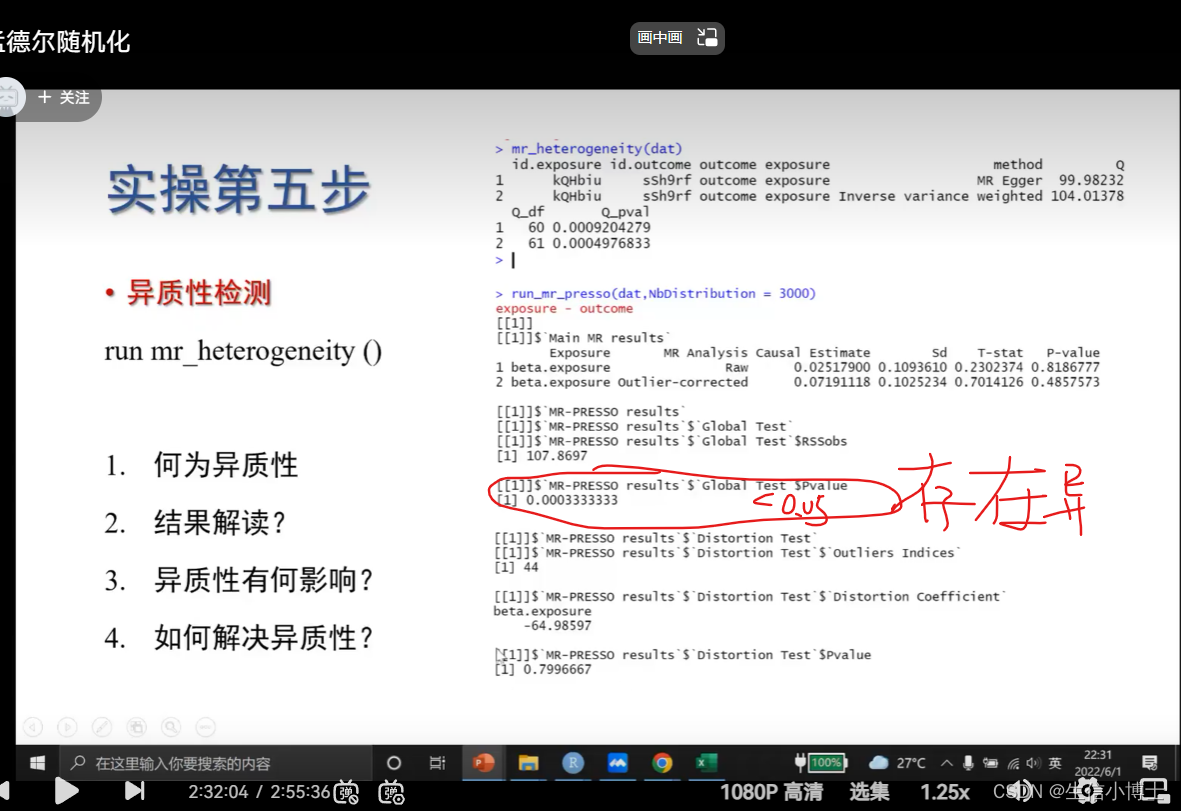这个离群值对方向是否有影响  没影响则p>0.05 

l列出离群值  p小于0.05  则说明存在异质性

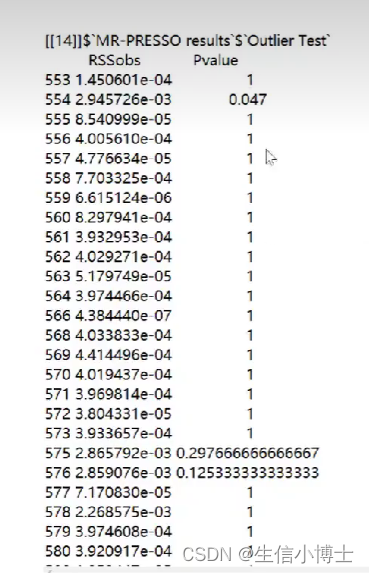
如果异质性很多，及时扔到几个snp，重新计算还是会有异质性的

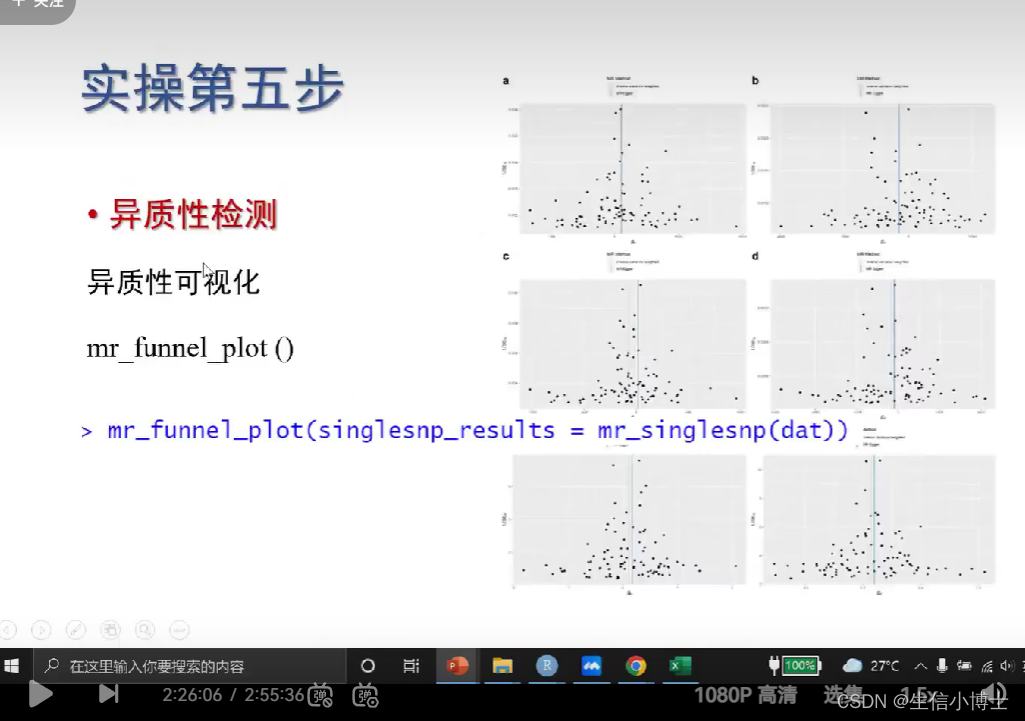
6.2 异质性可视化funnel plot

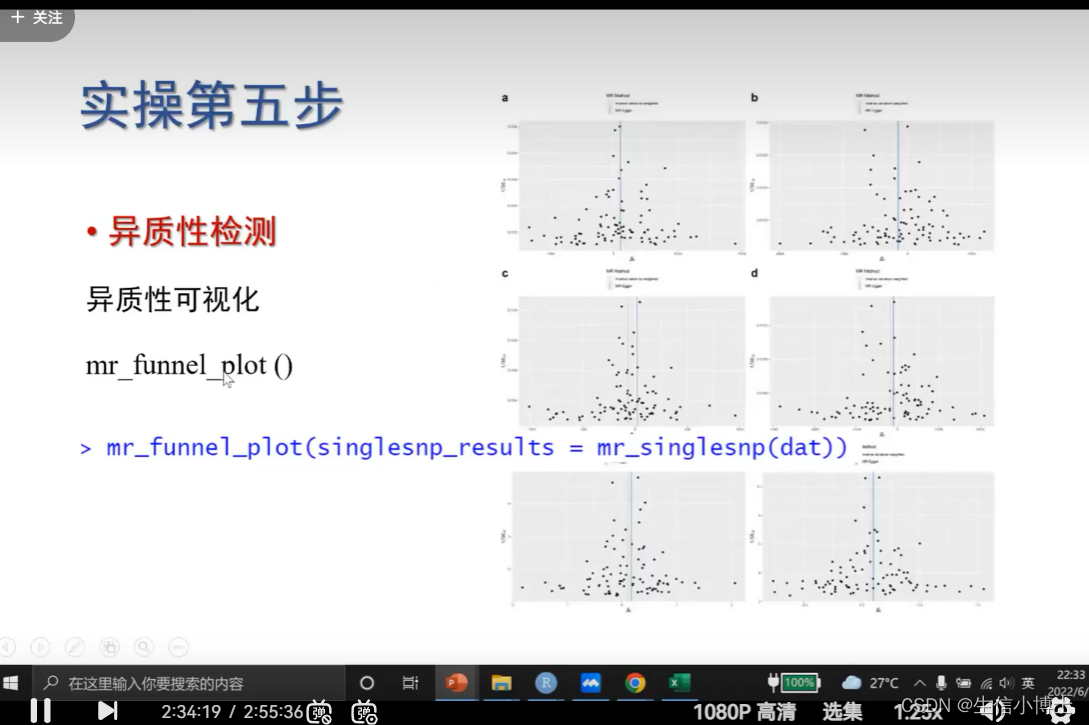
越对称 越好 

也会存在  ；即使不存在异质性  漏斗图也不对称

6.2 多效应 mr_pleiotropy_test()  结果不好就撤退，文章发不了

功能多效性 水平多效性

比如 snp可能通过别的表型作用于ad，而不是通过bmi这个表型来作用域ad

 0.078》0.05 没有多效性

使用egger_intercept来评估多效应

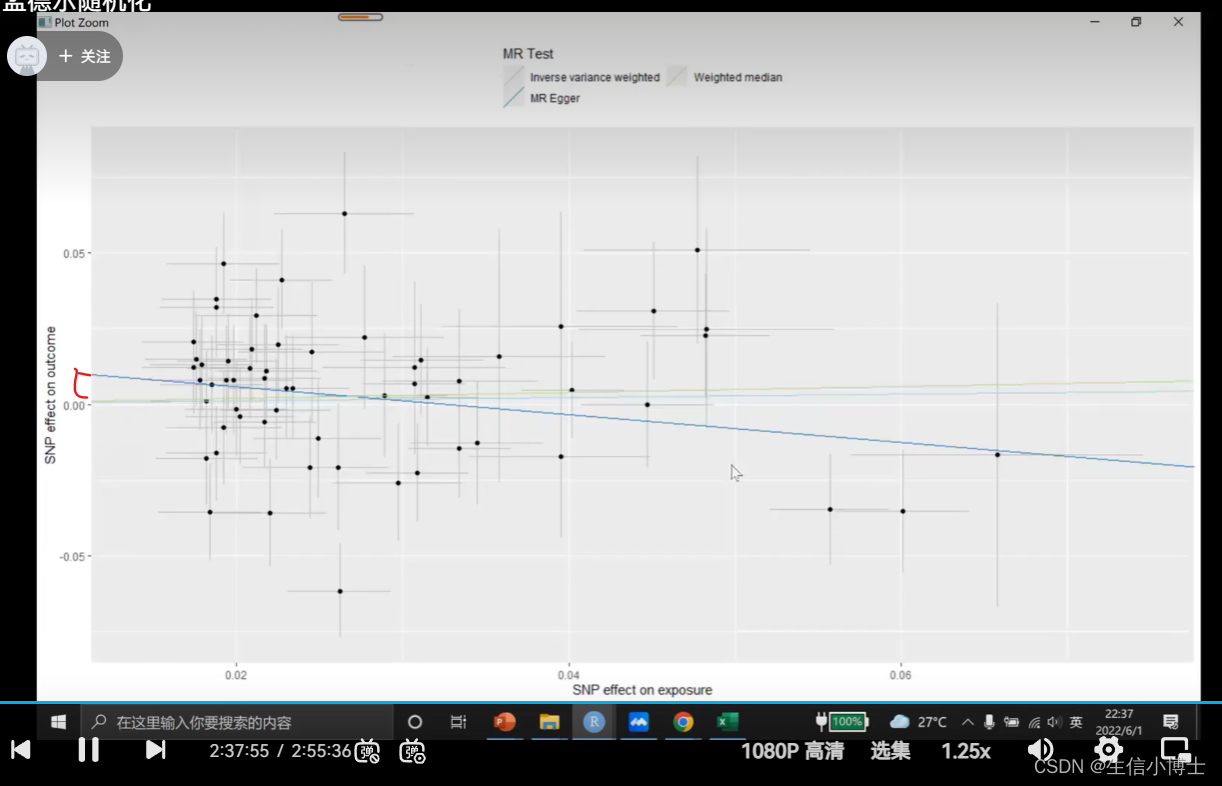
egger与y轴的截距 p值是来评估截距是否存在

如果p》0.05 ，则没有显著性，说明截距不存在

如果p《0.05，则有显著性。表明当snp为0时，对outcome存在非0的效应，说明snp可能通过影响其他表型来对结局产生影响。说明存在水平多效性。 这样的结果就不能使用

（snp对暴露的影响为0时，对结局仍产生非0影响，说明存在其他的中间因素来影响结局，具有水平多效性）

6.3 leave-one-out 

如果结果比较好，置信区间都应该再虚线的右边 

丢第第一个rs3817334时，剩下的snp再去做

总结

使用r来分析

1 提取暴露数据 

2 导入结局数据 

 

后续都一样 

筛查snp的第二表型 如果存在第二表型 就要可能需要筛掉它

7 统计学效能计算 power

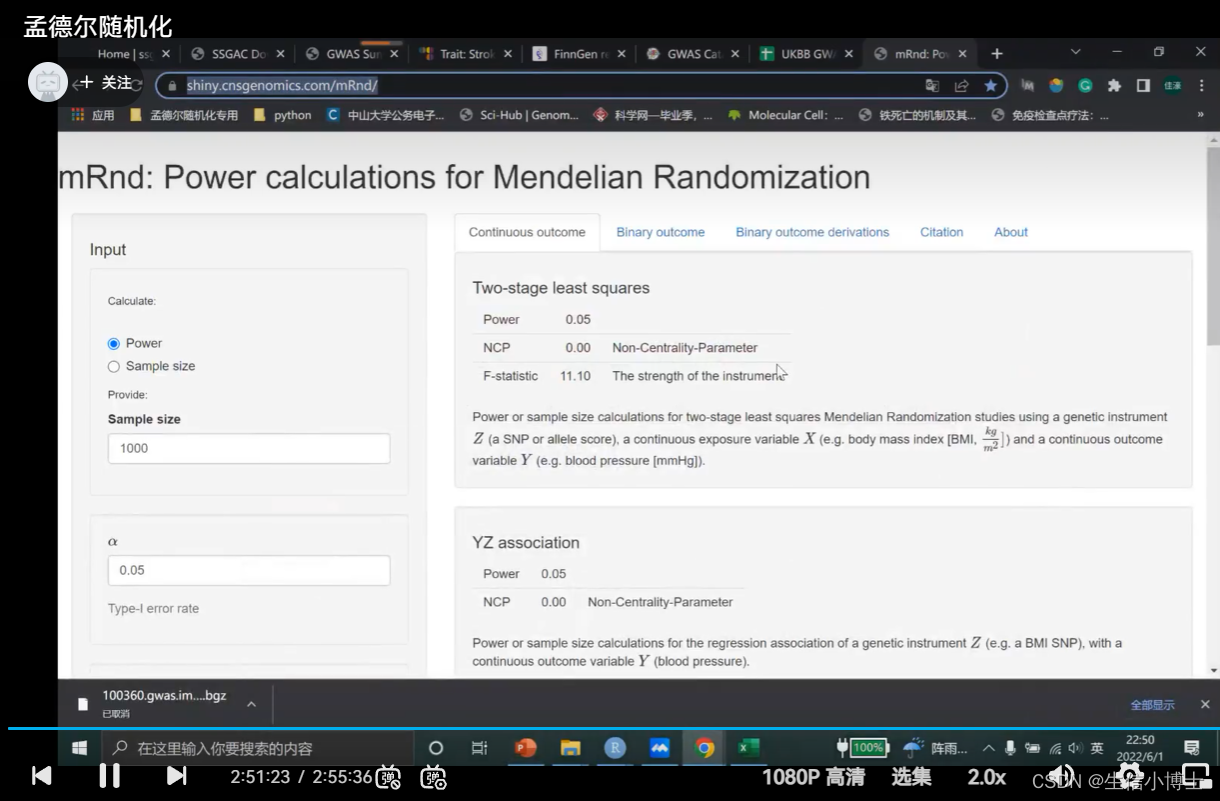
sample size 是总样本量

 a默认0.05

k 病例数所占总数的比例

or值为计算出来的值

  r2 是所有snp（60个）的r2加起来的值