LeetCode209.长度最小的子数组（滑动窗口法、暴力法）

LeetCode209.长度最小的子数组

1.问题描述
2.解题思路
3.代码
4.知识点

1.问题描述

给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。
力扣题目链接

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

进阶：

如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

2.解题思路

暴力解法：一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。时间复杂度很明显是O(n^2)。目前使用暴力法已经在LeetCode不能通过了，用时过长。
滑动窗口（双指针）：不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
1. 由于暴力法用时长，于是要找出能在一个for循环里完成的方法。
2. 那么一个for循环，需要考虑从起始位置还是终止位置开始。如果只用一个for循环表示滑动窗口的起始位置，那么又会陷入暴力解法的思路。那么，想到，在只用一个for循环的基础上，循环的索引表示滑动窗口的终止位置，通过调节起始位置来改变窗口大小。
3. 搞定终止位置的滑动，考虑起始位置如何滑动。
  
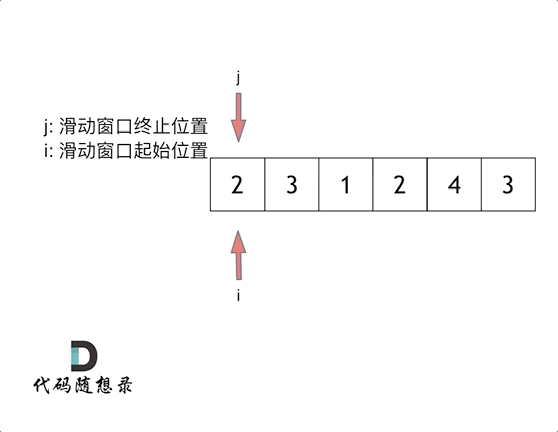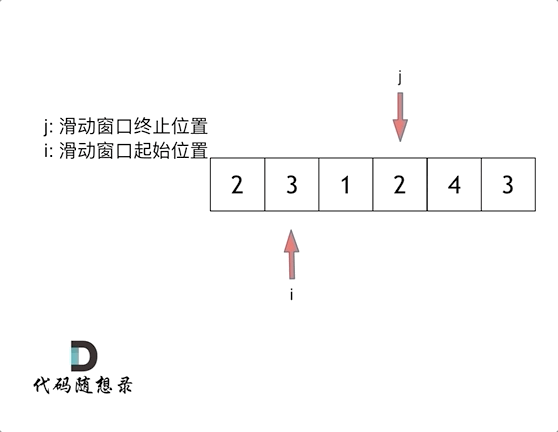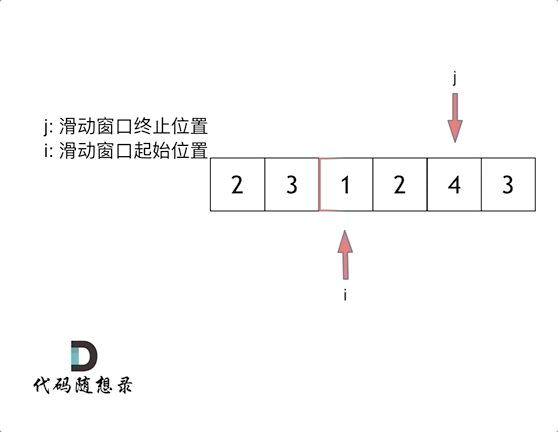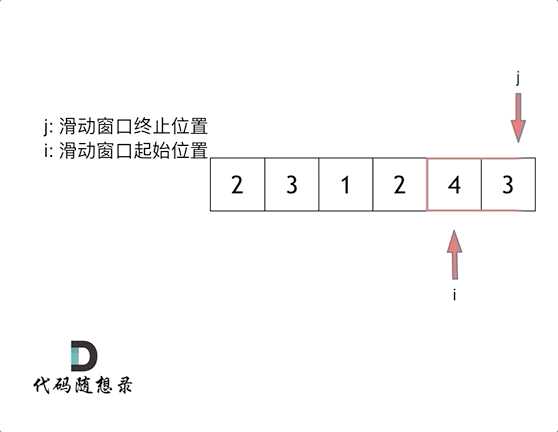
  总体思路如上述，结果也就是滑动窗口的确定，这是关键
  1. 窗口就是满足其和 ≥ target 的长度最小的连续子数组。
  2. 窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。
  3. 窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。
    
    滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
    - 时间复杂度：O(n)每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。
    - 空间复杂度：O(1)

3.代码

python：滑动窗口

from typing import Listclass Solution:def minSubArrayLen(self, target: int, nums: List[int]) -> int:# 初始化最小长度为数组长度加一# 或者为 min_len = float('inf')  将变量min_len初始化为正无穷大。min_len = len(nums) + 1left, right = 0, 0# 遍历过的总和，该值要与target进行比较cur_sum = 0# 双指针遍历数组while right < len(nums):# 将当前元素加入子数组总和cur_sum += nums[right]# 当当前子数组和大于等于目标值时，更新最小长度while cur_sum >= target:# 更新最小长度min_len = min(min_len, right - left + 1)cur_sum -= nums[left]  # 将左指针对应的值从当前和中减去left += 1  # 左指针右移一位right += 1  # 右指针右移一位# 如果最小长度未被修改，说明没有符合条件的子数组，返回0，否则返回最小长度return 0 if min_len == len(nums) + 1 else min_lentarget = 7
nums = [2, 3, 1, 2, 4, 3]
# 创建Solution类的实例
solution = Solution()
result = solution.minSubArrayLen(target, nums)
print(result)

python:暴力法

from typing import Listclass Solution:def minSubArrayLen(self, target: int, nums: List[int]) -> int:# 获取数组长度l = len(nums)# 初始化最小长度为数组长度加一min_len = len(nums) + 1for i in range(l):cur_sum = 0for j in range(i, l):cur_sum += nums[j]if cur_sum >= target:min_len = min(min_len, j - i + 1)break# 如果最小长度未被修改，说明没有符合条件的子数组，返回0，否则返回最小长度return 0 if min_len == len(nums) + 1 else min_lentarget = 7
nums = [2, 3, 1, 2, 4, 3]
# 创建Solution类的实例
solution = Solution()
result = solution.minSubArrayLen(target, nums)
print(result)

C++：滑动窗口

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;class Solution {public:int minSubArrayLen(int target, vector<int>& nums) {int min_len = nums.size() + 1;  // 初始化最小长度为数组长度加一int sum = 0;  // 初始化和为0int left = 0;  // 定义左边界for (int right = 0; right < nums.size(); right++) {  // 遍历数组sum += nums[right];  // 累加当前元素到和中while (sum >= target) {  // 若和大于等于目标值min_len = min(min_len, right - left + 1);  // 更新最小长度sum -= nums[left];  // 移动左边界并更新和left++;  // 左边界右移}}return min_len == nums.size() + 1 ? 0 : min_len;  // 若最小长度未被修改，返回0，否则返回最小长度}
};int main() {Solution sol;vector<int> nums = {2, 3, 1, 2, 4, 3};int target = 7;int result = sol.minSubArrayLen(target, nums);  // 调用minSubArrayLen方法cout << "最小子数组长度为：" << result << endl;  // 输出结果return 0;
}

C++：暴力

#include <iostream>
#include <vector>
using namespace std;class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int l = nums.size();  // 获取数组长度int min_len = l + 1;  // 初始化最小长度为数组长度加一for (int i = 0; i < l; i++) {int cur_sum = 0;  //  遍历过的总和，该值要与target进行比较for (int j = i; j < l; j++) {cur_sum += nums[j];  // 累加当前元素到和中if (cur_sum >= target) {  // 若和大于等于目标值min_len = min(min_len, j - i + 1);  // 更新最小长度break;  // 跳出内层循环}}}return min_len == l + 1 ? 0 : min_len;  // 若最小长度未被修改，返回0，否则返回最小长度}
};int main() {int target = 7;vector<int> nums = {2, 3, 1, 2, 4, 3};Solution solution;int result = solution.minSubArrayLen(target, nums);  // 调用minSubArrayLen方法cout << result << endl;  // 输出结果return 0;
}