2019年五一杯数学建模

A题 徐州潘安湖风景区游览路线设计

原题再现

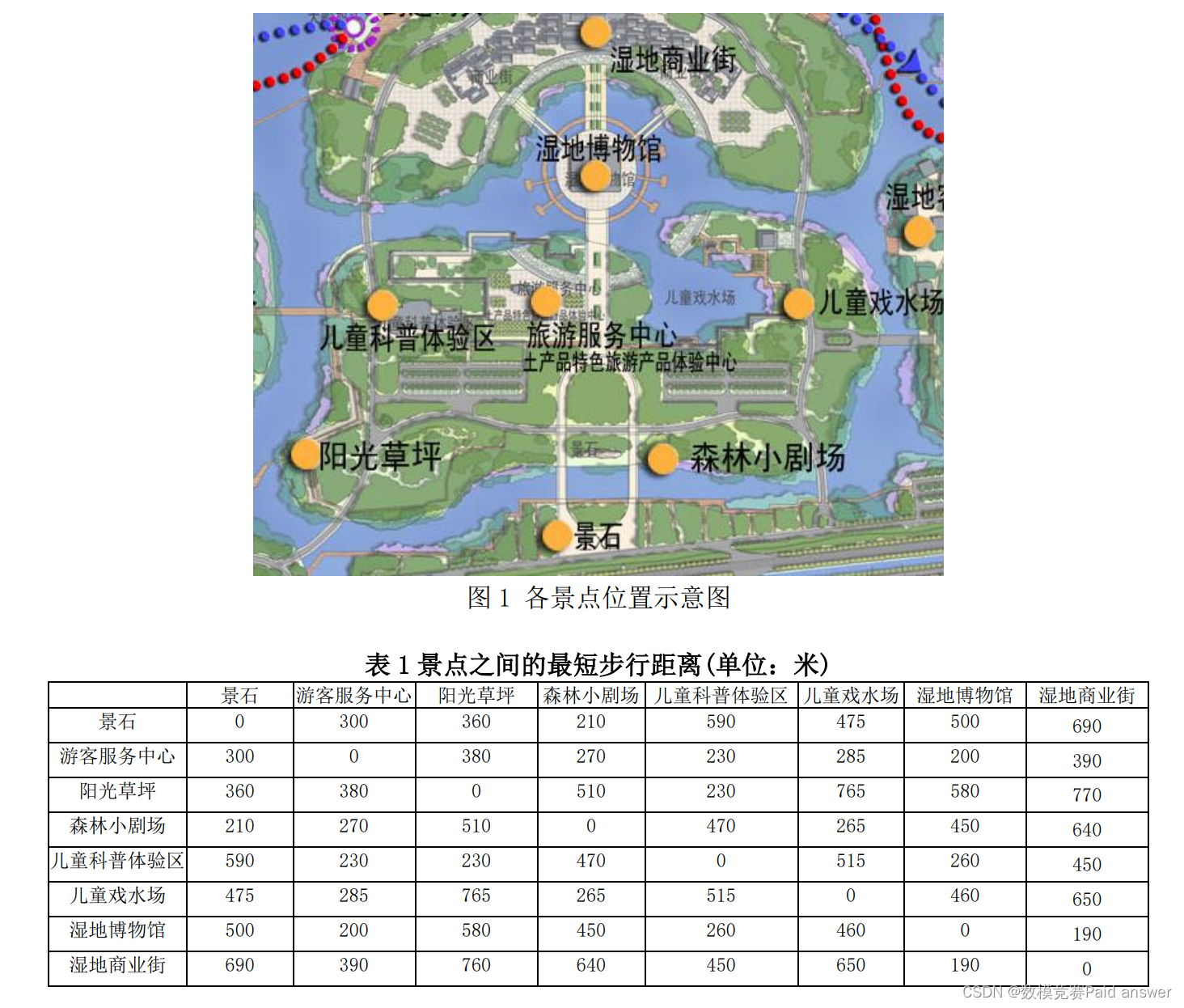
  徐州是一个老工业基地和资源型城市，煤炭开采历史长达130年。长期煤炭开采在徐州累计形成采煤塌陷区达数十万亩。位于徐州市贾汪区西南部、紧邻马庄的潘安湖湿地公园原来就是徐州最大的、塌陷最严重的采煤塌陷区。据统计，1949年以来，贾汪煤田累计为国家提供原煤3.5亿余吨, 也造成了11.3万亩土地塌陷。2010年，江苏省单体投资最大的一宗土地整理项目在潘安湖启动，即利用采煤塌陷形成的开阔水面，同步展开基本农田整理、采煤塌陷地复垦、生态环境修复等，在一片废墟上建成一个6500亩湖面的国家级水利风景区。2016年，贾汪被列为“国家全域旅游示范区”首批创建单位，全区共接待游客560万人次，旅游综合收入达到16.8亿元。本题选取潘安湖景区的部分景点(如图1所示)，请在如下的假设下，完成徐州潘安湖风景区游览路线设计问题。
  假设：
  （1）任意两个景点之间的最短步行距离如表1给出。
  （2）第二问、第三问假设步行速度 。
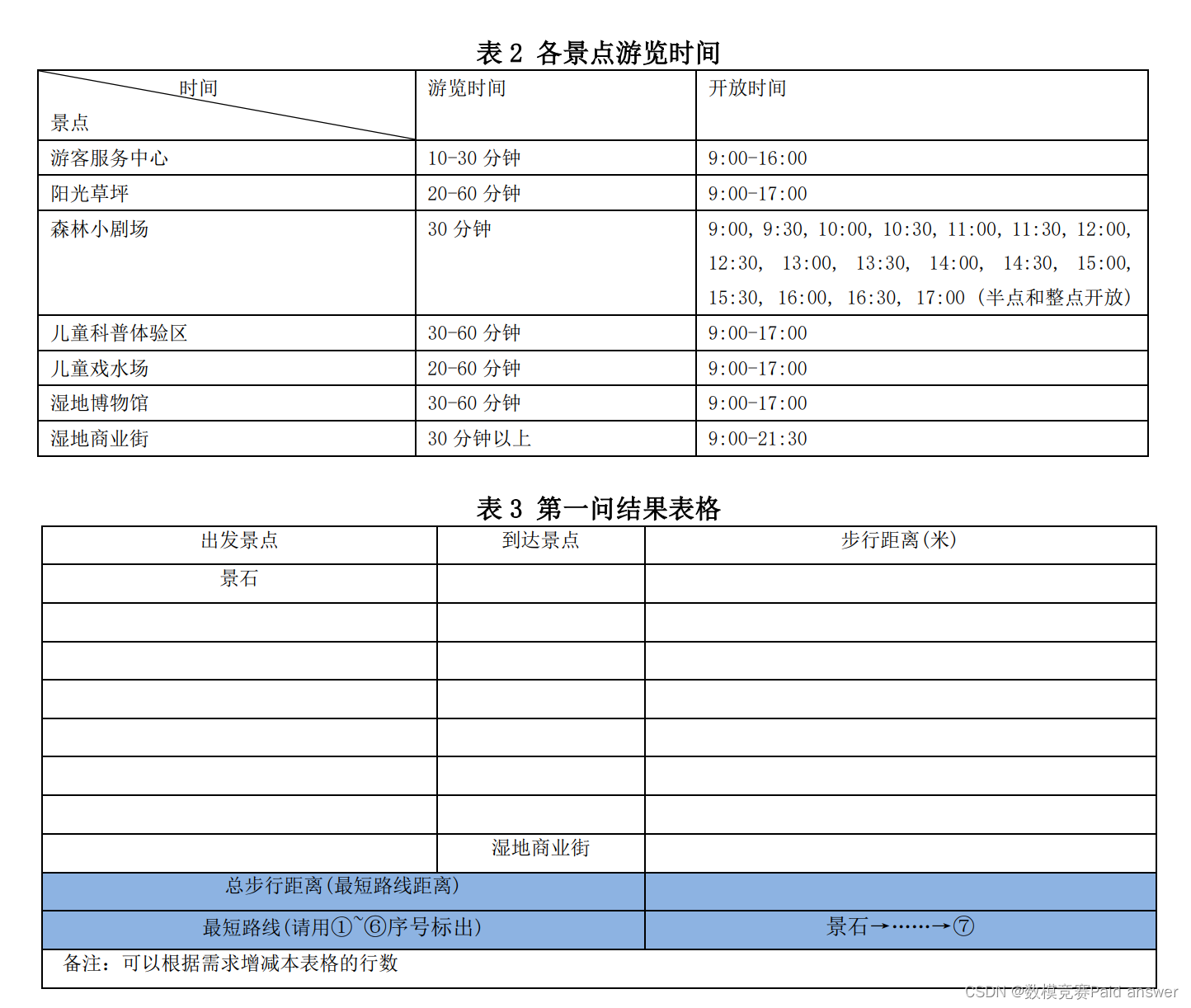
  （3）游客在景区停留的时间由“景点之间的步行时间”、“景点游览时间（即在景点内游玩的时间）” 和“在景区外的等待时间”三部分组成，其他时间忽略不计，游览时间必须符合表2的要求。

  1. 从景石出发，步行游览以下景点: ①游客服务中心，②阳光草坪，③森林小剧场，④儿童科普体验区，⑤儿童戏水场，⑥湿地博物馆，⑦湿地商业街。建立数学模型，找出从景石出发，到达⑦湿地商业街，并且经过①—⑥所有景点至少1次的距离最短的路线，计算该路线的长度，并将相关结果填入表格3。注：在每个景点不用停留。

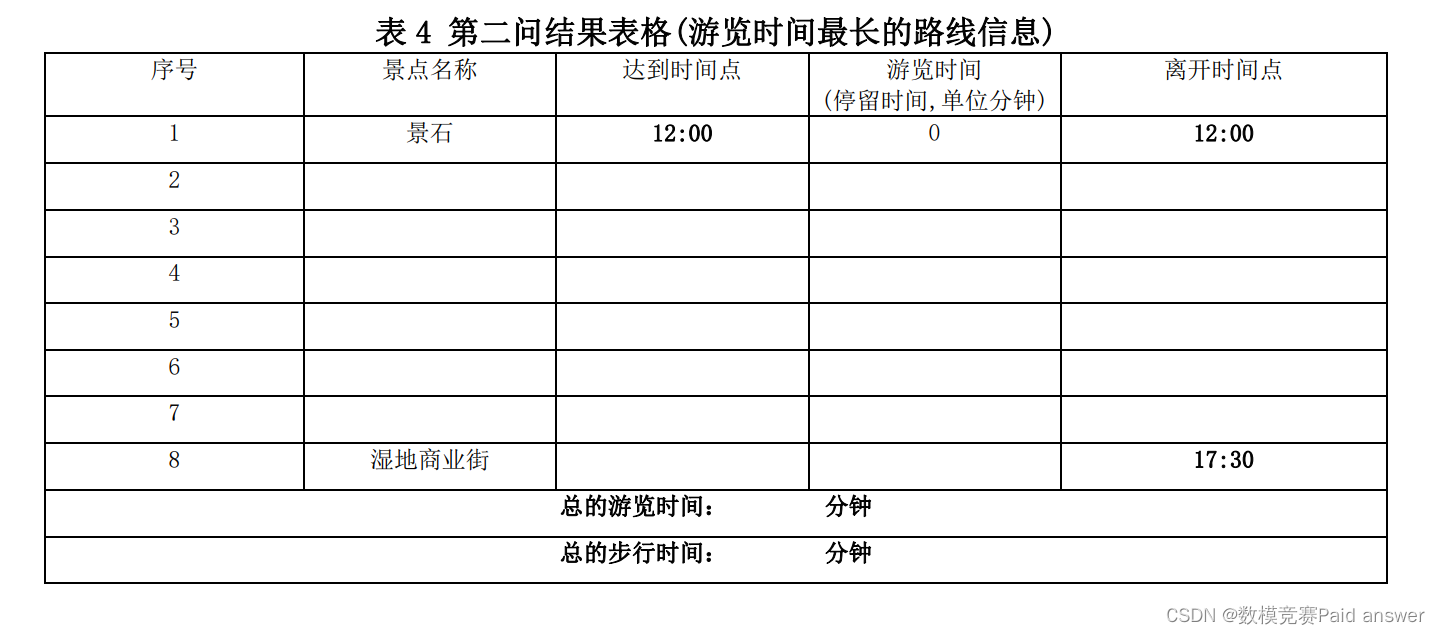
  2. 如果某游客12:00从景石出发，要求他17:00前到达湿地商业街，17:30离开湿地商业街(注：根据表2的要求在湿地商业街游览时间至少为30分钟)。建立数学模型，为该游客设计一条能游览完全部景点(景点①—⑦)且游览总时间最长的游览路线（假设在各个景点没有等待时间），并完成表4的填写。

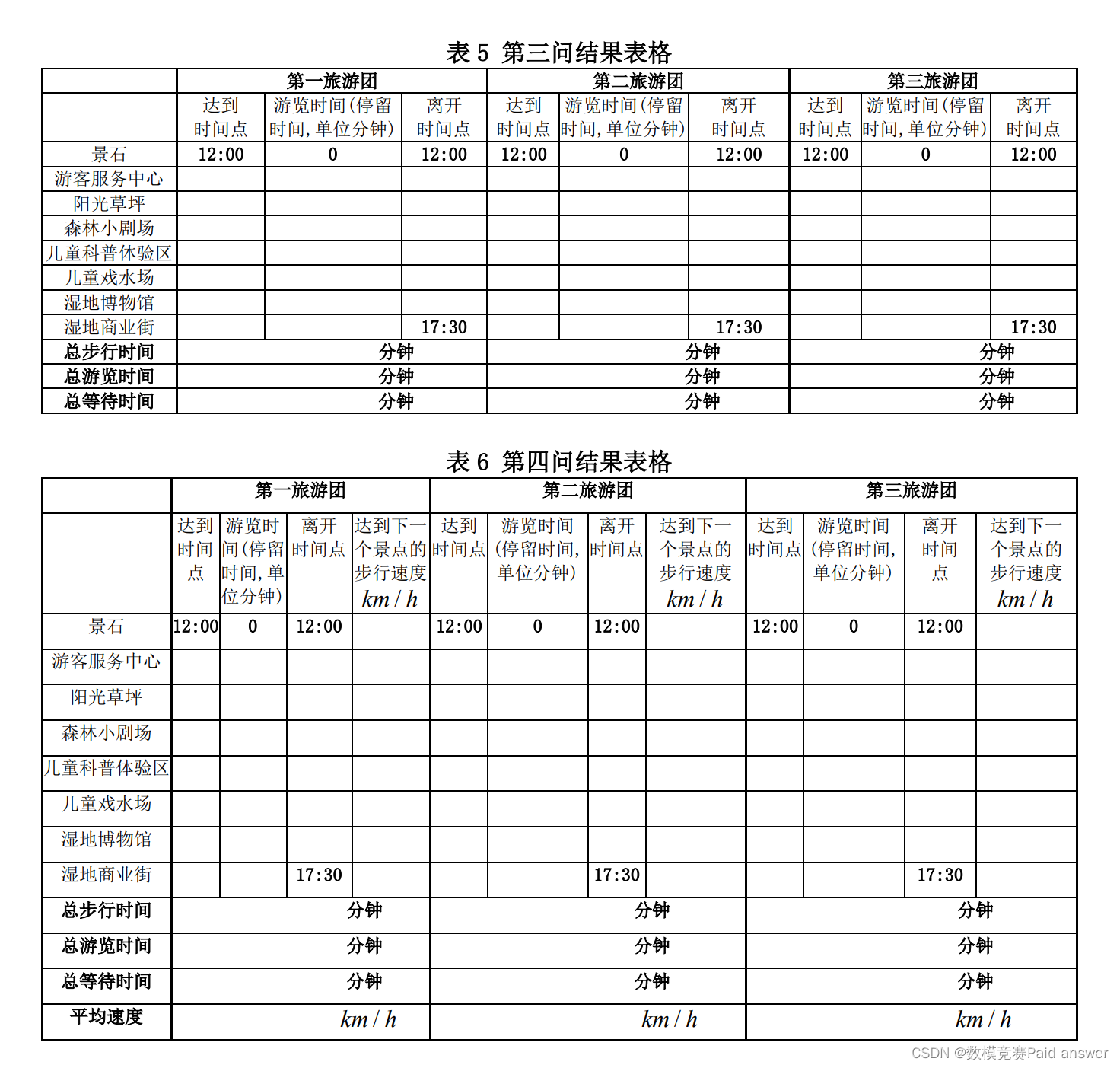
  3. 如果有3个旅游团，12:00同时从景石出发，要求三个旅游团17:00前到达湿地商业街，17:30离开湿地商业街(注：根据表2的要求在湿地商业街游览时间至少为30分钟)，并且每个景点（湿地商业街除外）同时只能容纳1个旅游团游览，按照时间顺序后到达的旅游团，需要等待先到达的旅游团游览结束之后才能开始游览。建立数学模型，为三个旅游团分别设计一条能游览完全部7个景点且游览总时间最长的游览路线，并完成表5的填写。

  4. 假设3个旅游团的步行速度可以在1km/h到3km/h之间调节，但是总的平均步行速度不能超过 ，3个旅游团12:00同时从景石出发，要求三个旅游团17:00前到达湿地商业街，17:30离开湿地商业街(注：根据表2的要求在湿地商业街游览时间至少为30分钟)，并且每个景点（湿地商业街除外）同时只能容纳1个旅游团游览，按照时间顺序后到达的旅游团，需要等待先到达的旅游团游览结束之后才能开始游览。建立数学模型，为三个旅游团分别设计一条能游览完全部7个景点且游览总时间长，总的等待时间短的游览路线，并完成表6的填写。

  5. 在现实中，考虑如下两个不确定性因素
  (1) 不同旅游团从景石出发的时间具有不确定性，例如，多个旅游团在不同的时间从景石出发开始游览，在此情况下到达湿地商业街的时间可以顺延。
  (2) 每个景点的等待时间也存在不确定性因素，例如，旅游设施短时间的维护和清理，或者受到散客客流的影响。
  考虑上述两个不确定性因素，其它条件与问题4相同，建立数学模型，为多个旅游团分别设计一条能游览完全部7个景点且游览总时间长，总的等待时间短的游览路线。

整体求解过程概述(摘要)

  本文针对徐州潘安湖风景区的部分景点展开游览路线规划的研究，通过将问题图论化，TSP 问题的转化等，建立了最短路线模型，混合整数 0-1 规划模型，双目标混合整数规划模型等，运用了 lingo 算法，穷举法等得到了受时间约束的游览路线方案，并对结果进行了误差分析和相关验算。
  问题一中，针对游览全部景点的最短路线规划问题，首先将问题图论化，将问题与 TSP 问题有机结合起来，通过引入 0-1 决策变量，建立了以线路距离最短为目标的 0-1 整数规划模型，利用 Lingo 软件求得总的步行距离为 1820 米，路线则为：景石→③→⑤→①→②→④→⑥→⑦。此外，我们还对不含有子巡回的约束条件表达式进行了严格的数学证明。
  问题二中，由于游客在时间上存在约束，针对游览时间最长的路线规划问题，基于问题一，又因为总时间是由游览的总时间、景点之间的步行时间、在景区外的等待时间三部分组成。通过引入决策变量，建立了以总游览时间最长为目标的 0-1混合整数规划模型，利用 Lingo 软件求得总游览时间为 270 分钟，总步行时间为 60分钟，路线为：景石→②→④→③→⑤→①→⑥→⑦。
  问题三中，针对 3 个旅游团的路线规划问题，通过顺延在景点外的等待时间来进行约束，由于每个景点只能容纳一个旅游团，基于问题二，建立了以总的游览时间最长为目标的混合 0-1 整数规划模型，采取穷举搜索结合 Lingo 软件的方法，求得最优结果：三个旅游团的最长的游览总时间分别为 270、261.9、268.8 分钟，而总步行时间分别是 60、68、61 分钟，无等待时间。此外，我们还利用 C 语言程序对各个旅游团在各个景点的时间节点是否冲突进行了验证，确保了结果的准确性。
  问题四中，根据对各个旅行团的速度和平均速度的变化，基于问题三，建立了以游览总时间最长，总的等待时间最短为双目标的混合整数规划模型，仍然采取穷举搜索结合 Lingo 软件的方法，求得最优结果：3 个旅游团总游览时间分别为 270、268.8、268.8 分钟，总的步行时间分别为 60、61.2、61.2 分钟，且平均速度满足2km/h，并用 C 语言冲突验证程序对结果的正确性进行了验证，特别注意的是 3 个旅行团的路线规划中有重复的路线选择，但每个旅游团在各个景点的游览时间并没有冲突。
  问题五中，由于考虑了两个不确定因素：①不同旅游团从景点 1（景石）出发的时间具有不确定性；②每个景点的等待时间也存在不确定性。假设存在 n 个旅游团，基于问题四，建立了双目标的混合整数规划模型，并设定了数据进行了试算，得到可行的参考方案。

模型假设：

  （1）假设正常情况下人的步行速度为V =2km/h。
  （2）假设游客在景区停留的时间由“景点之间的步行时间”、“景点游览时间（即在景点内游玩的时间）” 和“在景区外的等待时间”三部分组成，其他时间忽略不计。
  （3）假设在游玩过程中，游客们不会遇到突发事件，所有的游览均是正常进行。
  （4）假设每个景点的旅游设备的维护与清理都不会影响游客们的正常游览时间。

问题分析：

  背景
  在前期的准备工作中，我们发现本问题与 TSP 问题有着相应的联系，并且可以用混合整数规划来替代，此外问题的图论化也是一个需要了解的方面，图论化会将许多现实中的实际问题简单化，对于此类问题的研究有着积极的作用。
  所需问题的分析
  （1）根据问题一的说明，从景点 1（景石）出发，必须经过景点 2 至 7 至少一次，最后到达景点 8（湿地商业街），则可联想到问题的图论化，有利于我们对于路线筛选的准确性。此外图的连接也是一个需要解决的问题，需要连接 8 处景点，且必须从景点 1进，景点 8 出。如果能将本问题的 TSP 模型转换成混合整数规划，则可通过相应的约束条件结合目标函数利用 Lingo 软件得出最短的路线及长度。
  （2）根据问题二的说明，必须中午 12:00 从景石出发，17:30 离开湿地商业街，则总的时间为 330 分钟，有根据表 2 给出的相应游览时间以及景点开放时间，我们需要对这些时间进行约束，结合问题一建立的模型，找出游览全部景点的路线，而总时间又由景点之间的步行时间，景点游览时间，和在景点外的等待时间三部分组成，则我们可以得到游览的总时间=总时间 - 景点之间的步行时间 - 在景区外的等待时间。而通过路程时间计算公式，在已知总路线长度的前提下，可以求出景点之间的步行时间；景点外等待的时间只有在景点 4（森林小剧场）才会出现，再对比路线的规划，求出到达景点4（森林小剧场）时所耗的总时间，即可推算出到达景点 4（森林小剧场）的时间，从而对比相应时间段的开放时间，则可求出在景点外的等待时间，即运用公式，可得出游览的总时间，即为目标函数。
  （3）根据问题三的说明，若现有3个旅行团，同时从景点1出发，且时间同为12:00，并于 17:00 前均到达景点 8，然后于 17:30 离开。而问题三就是在问题二的基础上增加一个变量，关于旅行团的编号。但是每个景点只能容纳 1 个旅游团，且按照时间顺序后到达的旅游团需等到先到达的团队游览结束后才能开始游览，则不同于问题二的相关约束就只是多了一个变量即旅行团的编号。同时对于每个景点只能容纳一个旅游团，那就只好通过增加在景点外的等待时间来实现这一问题的约束，从而建立相关模型与目标函数，总结出总的约束条件，得出 3 个旅行团对应的游览路线与时间规划。
  （4）根据问题四的说明，表明在问题三的基础上设置了对游客步行速度的限制，即旅行团的步行速度在 1km/h 到 3km/h 之间调节，但是总的平均速度不能超过 2km/h，则只需再引入一个变量速度，在满足平均速度和各自旅行团的步行速度的约束下，就可以将总的约束条件分析完毕，但是问题四中的目标函数为双目标函数，既要分配三个旅游团的游览总时间长的路线，也要总的等待时间短的同一游览路线，所以就可以建立混合整数规划模型来得出双目标函数下的结果。
  （5）根据问题五的说明，只是在问题四条件的基础上考虑了两个不确定因素：①不同旅游团从景点 1（景石）出发的时间具有不确定性；②每个景点的等待时间也存在不确定性。为此可以设立一个不确定因素 Ek 来表明第 k 个旅游团在每个景点的不确定等待时间；再给出一个常量Yk 来表明第 k 个旅游团从景点 1（景石）出发的时间。又因为题设中只说明了多个旅行团，即表明可以用 k 个旅行团来参与模型的建立（k 没有限制），再基于问题四，建立数学模型来完成考虑不确定因素的多个旅游团的路线选择的猜想。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

function W = incandadf( F,f )
%仅适用于无向图
%W是输出矩阵
%F是输入矩阵
%f=0时，表示邻接矩阵转关联矩阵，f=1表示关联矩阵转邻接矩阵
if f==0m=sum(sum(F))/2;n=size(F,1);W=zeros(n,m);k=1;for i=1:nfor j=i:nif F(i,j)~=0W(i,k)=1;W(j,k)=1;k=k+1;endendend
elseif f==1m=size(F,2);n=size(F,1);W=zeros(n,n);for i=1:ma=find(F(:,i)~=0);W(a(1),a(2))=1;W(a(2),a(1))=1;end
elsefprintf('f error');end
W;
endfunction W = mattransf( F,f )
%仅适用于有向图
%W是输出矩阵
%F是输入矩阵
%f=0时，表示邻接矩阵转关联矩阵，f=1表示关联矩阵转邻接矩阵
if f==0m=sum(sum(F));n=size(F,1);W=zeros(n,m);k=1;for i=1:nfor j=1:nif F(i,j)~=0W(i,k)=1;W(j,k)=-1;k=k+1;endendend
elseif f==1m=size(F,2);n=size(F,1);W=zeros(n,n);for i=1:ma=find(F(:,i)~=0);if F(a(1),i)==1W(a(1),a(2))=1;elseW(a(2),a(1))=1;endend
elsefprintf('f error');
end
W;
end

function [T c] = Fleuf1( d )
%d表示图的权值矩阵
%T表示边的集合
%c表示权重和
n=length(d);
b=d;
b(b==inf)=0;
b(b~=0)=1;
m=0;
a=sum(b);
eds=sum(a)/2;
ed=zeros(2,eds);
vexs=zeros(1,eds+1);
matr=b;
for i=1:nif mod(a(i),2)==1m=m+1;end
end
if m~=0fprintf('no');T=0;c=0;
end
if m==0vet=1;flag=0;t1=find(matr(vet,:)==1);for ii=1:length(t1)ed(:,1)=[vet,t1(ii)];vexs(1,1)=vet;vexs(1,2)=t1(ii);matr(vexs(1,2),vexs(1,1))=0;flagg=1;tem=1;while flagg[flagg ed]=edf(matr,eds,vexs,ed,tem);tem=tem+1;if ed(1,eds)~=0 && ed(2,eds)~=0T=ed;T(2,eds)=1;c=0;for g=1:edsc=c+d(T(1,g),T(2,g));endflagg=0;break;endendend
end
endfunction [ flag ed ] = edf( matr,eds,vexs,ed,tem )
flag=1;
for i=2:eds[dvex f]=flecvexf(matr,i,vexs,eds,ed,tem);if f==1flag=0;break;endif dvex~=0ed(:,i)=[vexs(1,i) dvex];vexs(1,i+1)=dvex;matr(vexs(1,i+1),vexs(1,i))=0;elsebreak;end
end
endfunction [dvex f] = flecvexf(matr,i,vexs,eds,ed,temp)
f=0;
edd=find(matr(vexs(1,i),:)==1);
dvex=0;
dvex1=[];
ded=[];
if length(edd)==1dvex=edd;
elsedd=1;dd1=0;kkk=0;for kk=1:length(edd)m1=find(vexs==edd(kk));if sum(m1)==0dvex1(dd)=edd(kk);dd=dd+1;ddl=1;elsekkk=kkk+1;endendif kkk==length(edd)tem=vexs(1,i)*ones(1,kkk);edd1=[tem;edd];for l1=1:kkklt=0;ddd=1;for l2=1:edsif edd1(1:2,l1)==ed(1:2,l2)lt=lt+1;endendif lt==0ded(ddd)=edd(l1);ddd=ddd+1;endendendif temp<=length(dvex1)dvex=dvex1(temp);elseif temp>length(dvex1)&&temp<=length(ded)dvex=ded(temp);elsef=1;end
end
end

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可