目录
- 一、穷举搜索
- 二、图的遍历算法
- (一)深度优先搜索(DFS)
- (二)广度优先搜索(BFS)
- 三、回溯法
- (一)回溯法的定义
- (二)回溯法的应用
- 四、分支限界法
- (一) 上界与下界
- (二) 分支限界法的定义
- (三)分支限界法的应用
- 五、回溯法与分支限界法的对比
一、穷举搜索
穷举搜索法也被称为穷举法,其基本思想是将问题的所有的候选解都枚举出来,然后对候选解按照某种顺序进行逐一枚举和检验,并从中找出符合问题要求的候选解作为问题的解。其优点是实现简单且易于理解,适合规模较小的问题,但当问题的规模较大时,由于需要运行问题所有的候选解消耗大量的时间,从而导致算法的效率大大降低。
二、图的遍历算法
图的遍历算法适合无向图和有向图,有两种方法可分为深度优先搜索(DFS)和广度优先搜索(BFS)。
(一)深度优先搜索(DFS)
深度优先搜索的定义
简单地说,图的深度优先搜索可概括为尽可能深地去搜索一个图,是一个递归的过程(需要用到栈存储),通过遍历邻接表或邻接矩阵的方式深入搜索一个图,直到访问完所有连通的顶点,若当前分支已经访问过,则会回溯到上一个顶点,继续搜索其他分支顶点,直到所有顶点被访问。
- 递归这一点就类似
树的先序遍历,先访问结点,然后递归向外层结点遍历,尽可能深地搜索一个图,都采用回溯算法。
图的深度优先搜索首先选取图中某一顶点vi,访问后,任意选取一个与vi邻接的顶点,且该顶点未被访问,……,继续重复该过程,直到图中所有与vi连通的顶点都被访问到;若还有顶点未被访问到,则另外选取一个未被访问的顶点再次作为起始点,重复以上步骤,继续直至图中所有结点被访问。
例如,对下面这个图,以顶点a为源点对该图进行深度优先遍历,求其一个遍历序列:
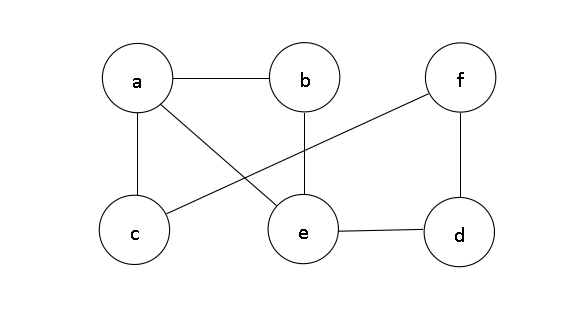
首先,选择与a邻接的任一顶点,由于与a邻接的顶点有b,c,e,可有以下三种访问序列{a,b,……}或{a,c,……}或{a,e,……},如下:
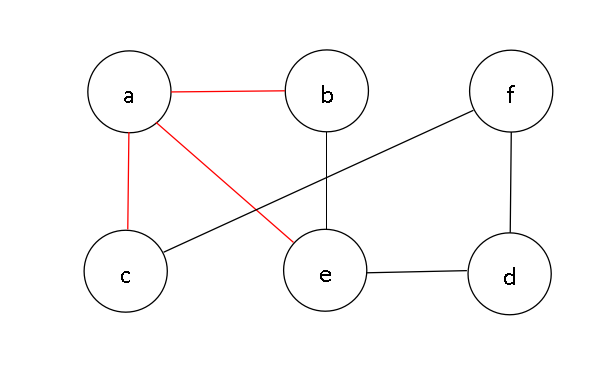
然后,选择访问顶点d,也可以选择还未被访问的顶点。由于先前选择访问的序列是{a,d},此时访问与顶点d相邻的顶点f,得到序列{a,d,f};再访问与顶点f相邻的顶点c,得到序列{a,d,f,c};由于此时与c邻接的顶点a和f都被访问过,回退到f,继续检查d,与d邻接的顶点也被访问过,……,最后直到顶点d还未被访问,访问它,可得到一个序列{a,e,d,f,c,b}。【序列不唯一】
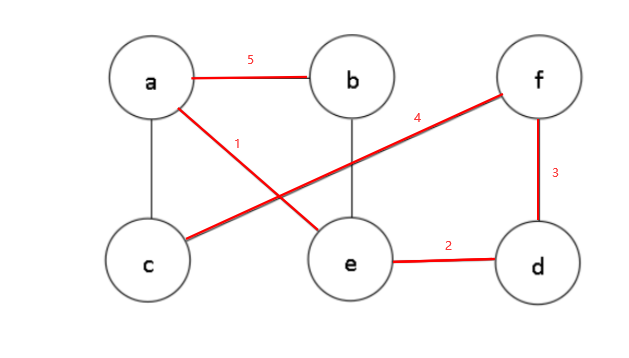
可看出a,e,d,f,c这段部分是该图中尽可能深地去搜索一个图的明显体现。
深度优先搜索的空间复杂度和时间复杂度
对于一个图G=(V,E),由顶点集V和边集E组成。
1、空间复杂度
- 由于DFS算法是一个递归算法,即递归遍历顶点集V,所以通过DFS遍历的空间复杂度为O(|V|)。
2、时间复杂度
- 时间复杂度取决于图的存储结构,若通过邻接矩阵表示图,则查找顶点的邻接顶点所需时间为O(|V|),总时间复杂度为O(|V2|)(邻接矩阵为方阵n×n);若通过邻接表表示图,则查找所有顶点的邻接顶点所需时间为O(|E|),访问顶点所需时间为O(|V|),即总时间复杂度为O(|V|+|E|)。
(二)广度优先搜索(BFS)
广度优先搜索的定义
广度优先搜索是通过队列来存储顶点实现遍历(队列用于避免重复访问,存放已经访问过的各邻接顶点),可以采用邻接表或邻接矩阵搜索,首先从起始点开始访问,将其邻接顶点依次入队,直到队列为空,从而访问到所有的顶点,即逐层遍历所有的顶点直到遍历完所有节点
- 逐层遍历这一点就类似
树的层序遍历,一层一层向外遍历。
图的广度优先搜索中首先选取一个起始点顶点vi,访问后将其入队并标记为已访问,当队列不为空时检查出队顶点的所有邻接顶点,访问未被访问的邻接顶点并将其入队,……,继续重复该过程,直到图中所有与vi连通的顶点都被访问到;当队列为空时跳出循环,则此时遍历完成。
例如,如下所示的图,从顶点1开始求一个广度优先搜索遍历序列:
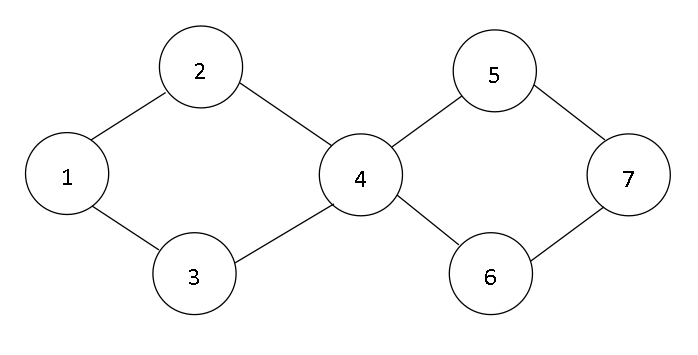
首先,选择与顶点1邻接的所有顶点进行访问,有2和3,可得序列{1,2,3}或{1,3,2};然后,再访问与2和3邻接的其他顶点,直到所有顶点被访问。例如,访问顶点2和3后,访问其邻接顶点4,然后再依次访问顶点4的邻接顶点5和6,最后访问顶点7,得到{1,2,3,4,5,6,7}。【序列不唯一】
广度优先搜索的空间复杂度和时间复杂度
对于一个图G=(V,E),由顶点集V和边集E组成。
1、BFS算法的空间复杂度
- 与深度搜索所需空间一样,通过BFS遍历的空间复杂度也为O(|V|)。
2、BFS算法的时间复杂度
- 时间复杂度取决于图的存储结构,若通过邻接矩阵表示图,则查找顶点的邻接顶点所需时间为O(|V|),总时间复杂度为O(|V2|)(邻接矩阵为方阵n×n),这和DFS算法的时间复杂度是一样的;若通过邻接表表示图,则每个顶点都入队一次,即所需时间为O(|V|),搜索顶点的邻接顶点所需时间为O(|E|),其时间复杂度为O(|V|+|E|)。
三、回溯法
(一)回溯法的定义
回溯法用到了上面的深度优先搜索(DFS)的思想,首先,通过穷举所有可能的解(明确搜索范围),从初始状态出发,以深度优先搜索来搜索问题的解,若当前结点不满足,则会退一步回溯到上一个结点尝试其他选择,直到最后找到包含问题解的结点。同样,若问题规模较大时,由于需要穷举所有可能的解,所以此时回溯法的搜索效率较低。【找出解空间树中满足约束条件的所有解】
注:递归算法与回溯法不是同一种思想,回溯法是穷举解空间树来找到满足条件的解的搜索算法思想,而递归是将大问题划分成小问题,然后通过递归以解决小问题来实现最终问题的解,运用了分治的思想。
回溯法的算法框架可分为三部分:
1、针对所给问题,定义问题的解空间;
2、确定易于搜索的解空间组织结构;
3、以深度优先搜索解空间,并在搜索过程中用剪枝函数(隐约束)避免无效搜索。
隐约束分为两种,一种是约束条件,用于判断是否能得到可行解,二是限界条件,用于判断是否能得到最优解。所以,从算法上来看,回溯法是一种带有约束函数(约束条件)或限界函数(限界条件)的深度优先搜索方法。
(二)回溯法的应用
回溯法常用解决排列问题、组合问题、子集问题、路径问题等等。
1、组合问题(组合树/满m叉树)
一组元素中有若干个元素,若将这些元素组合使其一起满足某种性质,该问题的所有组合(解空间树)是一棵满m叉树或组合树。例如一个满二叉树如下(m=2):
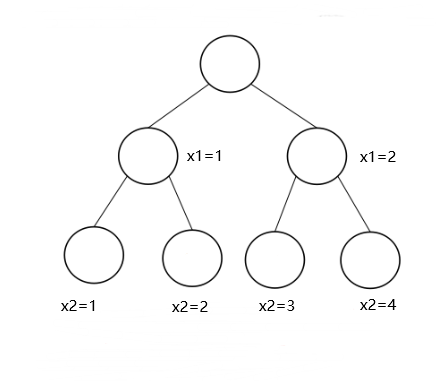
例如,一个满m叉树的实例:
对于一个有4个交通信号灯的道路,每个交通信号灯有3种可能的选择(红、黄、绿),需要找出一种选择,使得该道路满足某活动。该场景可以使用满三叉树来表示每个元素(交通信号灯)的选择情况,在满三叉树的每个节点上,有三个子节点,每个子节点代表一个元素(交通信号灯)的选择。如果选择了其中一个元素(交通信号灯),则可以将其对应的子节点标记为已访问,并将该节点加入到结果集中。当遍历完整个满三叉树后,可以得到所有可能的交通信号灯的组合,其中每个组合都满足某种性质,从而找到目标性质满足该活动。
2、排列问题(排列树)
在若干个元素的排列中,确定满足某种性质的一个排列时,该问题的所有排列(解空间树)是一棵排列树。例如,n个元素的排列数为n!(n的阶乘),若n=3,三个元素为{1,2,3},则其排列树如下:
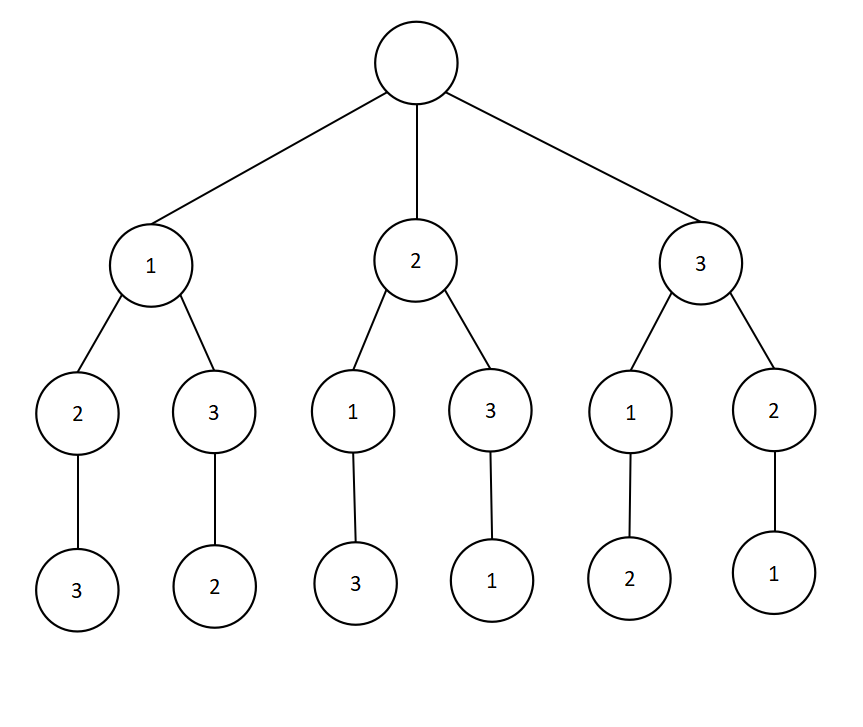
其中树的根结点为空,表示初始状态。
3、子集问题(子集树)
在若干个元素组成的集合S,确定满足某种性质的一个子集时,该问题的所有子集(解空间树)对应一个子集树。例如,0-1背包问题中,所要找到满足性质的子集为该子集中物品的重量不超过背包容量,且背包内总价值是最大的,该问题的解空间树是一棵子集树。子集树通常有2n个叶结点,其结点总个数为2(n+1)-1,是一棵完全二叉树。
在回溯法中,解向量<x1,x2,…,xn>可以表示为分量取值为{0,1}的比特串,解空间可以组成一颗完全二叉树,这棵搜索树被称为子集树。
四、分支限界法
(一) 上界与下界
对于一个待求解的问题,上界和下界是对问题的可能解进行限制和估计的方法,从而用于解决问题。上界相当于当前最高要求,指问题中的最优解不会超过某个已知值,下界相当于当前最低要求,指问题中的最优解不会低于某个已知值。
利用这一点,可以用于剪枝搜索树的分支,避免对不可能得到最优解的分支进行搜索,从而缩小了搜索空间,达到提高算法效率的目的。
(二) 分支限界法的定义
- 分支限界法也是一种搜索算法,简单的来说,分支限界法的
限界就是利用上界和下界来提高搜索效率。搜索解空间树中利用上界和下界的信息来剪枝搜索树的分支,舍弃导致不可行解或导致非最优解的分支。【找出解空间树中满足约束条件的一个解】
分支限界法中通常采用广度优先搜索(BFS),是以最大收益(最小耗费)的方式来搜索解空间树,其步骤如下:
①首先,将根结点加入活结点表,然后从其中取出,使其成为扩展结点;
②依次生成扩展结点的所有分支,即其孩子结点;
③判断每个孩子结点。通过计算孩子结点的上界和下界,并根据这些界限来决定是否继续搜索该分支,若某个分支的界限满足上界小于或等于下界,则可以剪掉该分支;否则,继续搜索该分支,直到找到满足要求的解或搜索完所有分支(继续通过扩展结点)。
(三)分支限界法的应用
分支限界法的应用场景有:
1、0-1背包问题
2、旅行商问题
旅行商问题指的是在一组给定的城市之间找到最短的路径,使得每个城市恰好被访问一次,最终回到起点。
3、集装箱装载问题
旅行商问题是一个经典的组合优化问题,可以使用分支限界法进行求解。通过搜索所有可能的路径组合,找到总距离最短的一条路径。
4、电路设计中的布线问题
电路设计中的布线问题可以使用分支限界法求解,通过搜索所有可能的布线方式,找到最优解。例如,在M×N的方格中,指定一个方格的中点为a,另一个方格的中点为b,找到a到b的最短路径(布线时只能走直线或直角边)。通过可以把布线的情况剪掉,将能布线的方格加入活结点表,扩展直到找到目标点或活结点表空为止。
五、回溯法与分支限界法的对比
- 回溯法的优点在于它能够找出所有可能的解,而不仅仅是最优解。而若对于大型问题,回溯法的效率可能较低,因为它需要穷举所有可能的解;分支限界法的优点在于它能够在问题规模较大时,通过剪枝有效地减少搜索空间,从而快速找到最优解,但不能保证找到所有的可能解。
| 搜索算法名称 | 回溯法 | 分支限界法 |
|---|---|---|
| 搜索解空间树方式 | 深度优先搜索(DFS) | 广度优先搜索(BFS) |
| 求解解空间树目的 | 找出满足约束条件的所有解 | 找出满足约束条件的一个解 |
| 活结点成为扩展结点 | 一次或多次 | 一次 |
回溯法的适用场景有:n皇后问题、子集树(0-1背包问题、最大团问题)、排列树(旅行商问题、批处理作业调度问题)、组合树(图的m着色问题)等等;
分支限界法的适用场景有:0-1背包问题、旅行商问题、集装箱装载问题、电路设计中的布线问题等等。






--安装)












