文章目录
- 一、最小二乘法
- 1.1 定义
- 1.2 SISO系统运用最小二乘估计进行辨识
- 1.3 几何解释
- 1.4 最小二乘法性质
- 二、加权最小二乘法
- 三、递推最小二乘法
- 四、增广最小二乘法
一、最小二乘法
1.1 定义
1974年高斯提出的最小二乘法的基本原理是未知量的最可能值是使各项实际观测值和计算值之间差的平方乘以其精确度的数值以后的和为最小。
z ( k ) = y ( k ) + v ( k ) z(k)=y(k)+v(k) z(k)=y(k)+v(k)
z ( k ) z(k) z(k)为观测值, y ( k ) y(k) y(k)为计算值, v ( k ) v(k) v(k)误差。
最小二乘法为 m i n ∑ k = 1 m w ( k ) ∣ z ( k ) − y ( k ) ∣ 2 min \ \sum_{k=1}^mw(k)|z(k)-y(k)|^2 min k=1∑mw(k)∣z(k)−y(k)∣2
w(k)为精确度。
通过一个例子来理解最小二乘法。
通过试验确定热敏电阻阻值和温度间的关系如下表所示:
| t(℃) | t 1 t_1 t1 | t 2 t_2 t2 | ⋯ \cdots ⋯ | t N − 1 t_{N-1} tN−1 | t N t_N tN |
|---|---|---|---|---|---|
| R( Ω \Omega Ω) | R 1 R_1 R1 | R 2 R_2 R2 | ⋯ \cdots ⋯ | R N − 1 R_{N-1} RN−1 | R N R_N RN |
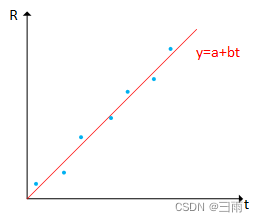
用直线 y = a + b t y=a+bt y=a+bt拟合该曲线,a和b为待估计参数。
每次测量总是存在随机误差。
y i = R i + v i y_i=R_i+v_i yi=Ri+vi
当采用每次测量的随机误差的平方和最小时,即
J m i n = ∑ i = 1 N v i 2 = ∑ i = 1 N [ R i − ( a + b t i ) ] 2 J_{min}=\sum_{i=1}^Nv_i^2=\sum_{i=1}^N[R_i-(a+bt_i)]^2 Jmin=i=1∑Nvi2=i=1∑N[Ri−(a+bti)]2
,平方运算又称二乘,而且又是按照J最小来估计a和b的,称这种方法为最小二乘估计算法,简称最下二乘法。
为什么用平方呢?因为平方可以求导。
利用最小二乘法求取模型参数
若使得J最小,利用求极值的方法得

整理得
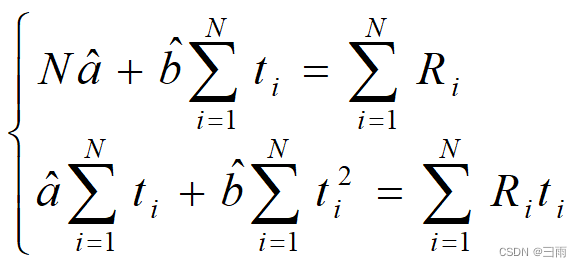
解方程组得
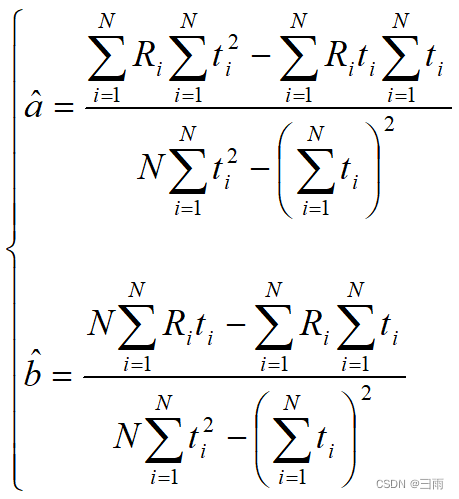
1.2 SISO系统运用最小二乘估计进行辨识
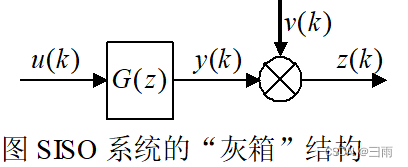
对于SISO系统,被辨识模型传递函数为:
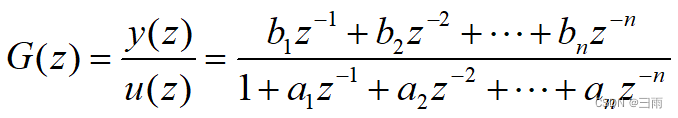
对其离散化,对应的差分方程为

若考虑噪声影响
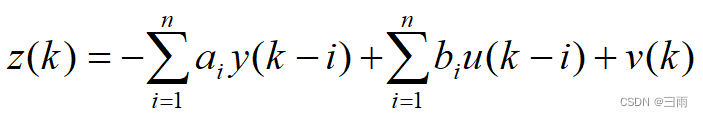
式中, z ( k ) z(k) z(k)为系统输出量的第 k k k次观测值; y ( k ) y(k) y(k)为系统输出量的第 k k k次真值; u ( k ) u(k) u(k)为系统的第 k k k个输入值; v ( k ) v(k) v(k)是均值为0的随机噪声。
定义


则 z ( k ) z(k) z(k)可写为
z ( k ) = h ( k ) θ + v ( k ) z(k)=h(k)\theta+v(k) z(k)=h(k)θ+v(k)
式中, θ \theta θ为待估计参数。
令 k = 1 , 2 , ⋯ , m k=1,2,\cdots,m k=1,2,⋯,m,则有



最小二乘的思想就是寻找一个 θ \theta θ的估计值 θ ^ \hat\theta θ^,使得各次测量的 Z i ( i = 1 , ⋯ , m ) Z_i(i=1,\cdots,m) Zi(i=1,⋯,m)与由估计 θ ^ \hat\theta θ^确定的量测估计 Z i ^ = H i θ ^ \hat{Z_i}=H_i\hat\theta Zi^=Hiθ^之差的平方和最小,即

根据极值定理:

如果 H m H_m Hm的行数大于等于行数,即 m ⩾ 2 n m\geqslant2n m⩾2n, H m T H m H_m^TH_m HmTHm满秩,即 r a n k ( H m T H m ) = 2 n rank(H_m^TH_m)=2n rank(HmTHm)=2n,则 ( H m T H m ) − 1 (H_m^TH_m)^{-1} (HmTHm)−1存在。则 θ \theta θ的最小二乘估计为
θ ^ = ( H m T H m ) − 1 H m T Z m \hat\theta=(H_m^TH_m)^{-1}H_m^TZ_m θ^=(HmTHm)−1HmTZm
1.3 几何解释
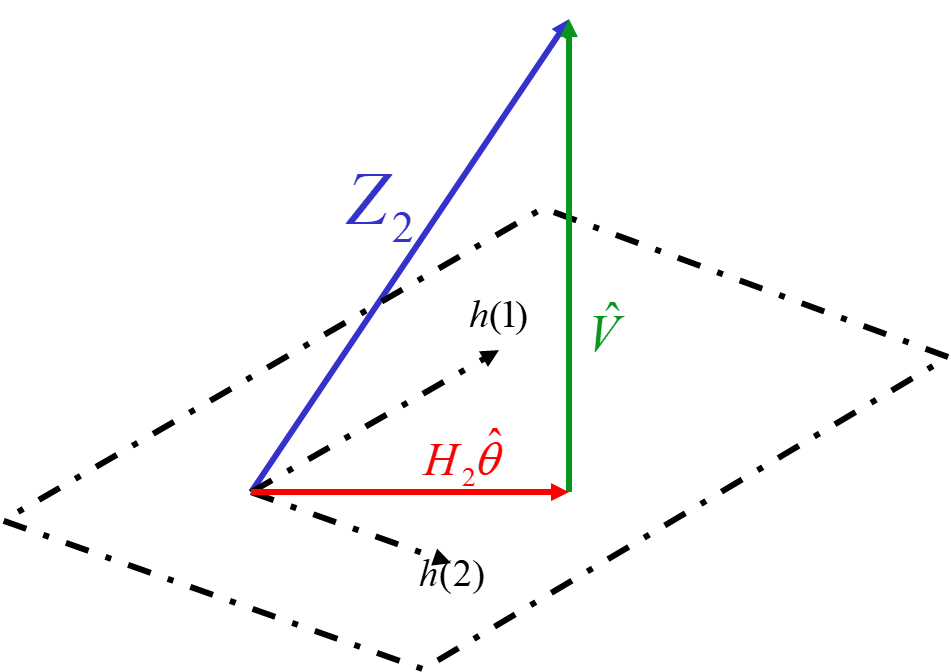
H m θ ^ H_m\hat\theta Hmθ^应该等于 Z m Z_m Zm在 h ( 1 ) , h ( 2 ) , ⋯ , h ( m ) {h(1),h(2),\cdots,h(m)} h(1),h(2),⋯,h(m)的张成空间的投影。
1.4 最小二乘法性质
- 最小二乘估计是无偏估计
如果参数估计的数学期望等于参数的真值,则称估计是无偏的。
E ( θ ^ ) = 0 或 E ( θ ~ ) = 0 E(\hat\theta)=0或E(\tilde\theta)=0 E(θ^)=0或E(θ~)=0 - 最小二乘估计是有效估计
有效估计就是具有最小方差的估计。
E ( θ ~ θ ~ T ) = ( H m T H m ) − 1 H m T R H m ( H m T H m ) − 1 最小 E(\tilde\theta\tilde\theta^T)=(H_m^TH_m)^{-1}H_m^TRH_m(H_m^TH_m)^{-1}最小 E(θ~θ~T)=(HmTHm)−1HmTRHm(HmTHm)−1最小 - 最小二乘估计是一致估计
如果随着测量次数 m m m的增加, θ ^ m \hat\theta_m θ^m依概率收敛于真值 θ \theta θ,则称 θ ^ m \hat\theta_m θ^m为 θ \theta θ的一致估计。
l i m m → ∞ p ( ∣ θ ^ m − θ ∣ > ε ) = 0 lim_{m\to \infty}p(|\hat\theta_m-\theta|>\varepsilon)=0 limm→∞p(∣θ^m−θ∣>ε)=0
二、加权最小二乘法
一般最小二乘估计精度不高的原因之一是对测量数据同等对待;由于各次测量数据很难在相同的条件下获得的,因此存在有的测量值置信度高,有的测量值置信度低的问题。对不同置信度的测量值采用加权的办法分别对待,置信度高的,权重取得大些;置信度低的,权重取的小些。
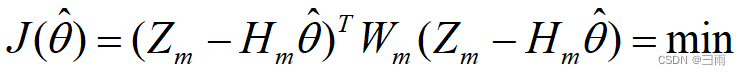
式中, W m W_m Wm为加权矩阵,它是一个对称正定矩阵,通常取为对角矩阵,即 W m = d i a g [ w ( 1 ) w ( 2 ) ⋯ w ( m ) ] W_m=diag[w(1)\ w(2)\cdots \ w(m)] Wm=diag[w(1) w(2)⋯ w(m)]

θ ^ = ( H m T W m H m ) − 1 H m T W m Z m \hat\theta=(H_m^TW_mH_m)^{-1}H_m^TW_mZ_m θ^=(HmTWmHm)−1HmTWmZm
如果 W m = R − 1 W_m=R^{-1} Wm=R−1
θ ^ = ( H m T R − 1 H m ) − 1 H m T R − 1 Z m \hat\theta=(H_m^TR^{-1}H_m)^{-1}H_m^TR^{-1}Z_m θ^=(HmTR−1Hm)−1HmTR−1Zm
又称马尔可夫估计。
马尔可夫估计的均方误差为
E ( θ ~ θ ~ T ) = ( H m T R − 1 H m ) − 1 E(\tilde\theta\tilde\theta^T)=(H_m^TR^{-1}H_m)^{-1} E(θ~θ~T)=(HmTR−1Hm)−1
马尔可夫估计的均方误差比任何其他加权最小二乘估计的均方误差都要小,所以是加权最小二乘估计中的最优者。
加权最小二乘估计也满足无偏性、有效性、一致性。
三、递推最小二乘法
当前估计值 θ ^ ( k ) \hat\theta(k) θ^(k)=上次估计值 θ ^ ( k − 1 ) \hat\theta(k-1) θ^(k−1)+修正项
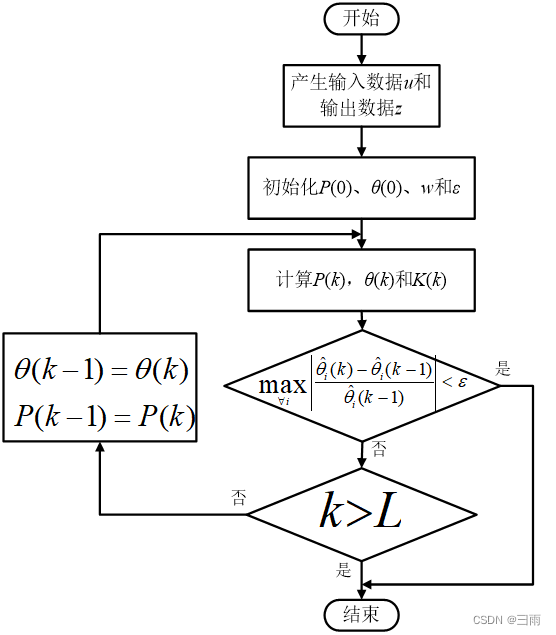
根据加权最小二乘法,利用 m 次测量数据所得到的估值
θ ^ = ( H m T W m H m ) − 1 H m T W m Z m \hat\theta=(H_m^TW_mH_m)^{-1}H_m^TW_mZ_m θ^=(HmTWmHm)−1HmTWmZm
当新获得一对输入、输出数据时
z ( m + 1 ) = h ( m + 1 ) θ + v ( m + 1 ) z(m+1)=h(m+1)\theta+v(m+1) z(m+1)=h(m+1)θ+v(m+1)
利用m+1次输入、输出数据,得到的方程为 Z m + 1 = H m + 1 θ + V m + 1 Z_{m+1}=H_{m+1}\theta+V_{m+1} Zm+1=Hm+1θ+Vm+1
θ ^ m + 1 = ( H m + 1 T W m + 1 H m + 1 ) − 1 H m + 1 T W m + 1 Z m + 1 \hat\theta_{m+1}=(H_{m+1}^TW_{m+1}H_{m+1})^{-1}H_{m+1}^TW_{m+1}Z_{m+1} θ^m+1=(Hm+1TWm+1Hm+1)−1Hm+1TWm+1Zm+1
W m + 1 = [ W m 0 0 w ( m + 1 ) ] W_{m+1}=\begin{bmatrix} W_m & 0 \\ 0 & w(m+1) \end{bmatrix} Wm+1=[Wm00w(m+1)]
如果设 P m = [ H m T W m H m ] − 1 P_m=[H_m^TW_mH_m]^{-1} Pm=[HmTWmHm]−1
P m + 1 = [ H m + 1 T W m + 1 H m + 1 ] − 1 P_{m+1}=[H_{m+1}^TW_{m+1}H_{m+1}]^{-1} Pm+1=[Hm+1TWm+1Hm+1]−1
则有 θ ^ m = P m H m T W m Z m \hat\theta_m=P_mH_m^TW_mZ_m θ^m=PmHmTWmZm
θ ^ m + 1 = P m + 1 H m + 1 T W m + 1 Z m + 1 \hat\theta_{m+1}=P_{m+1}H_{m+1}^TW_{m+1}Z_{m+1} θ^m+1=Pm+1Hm+1TWm+1Zm+1


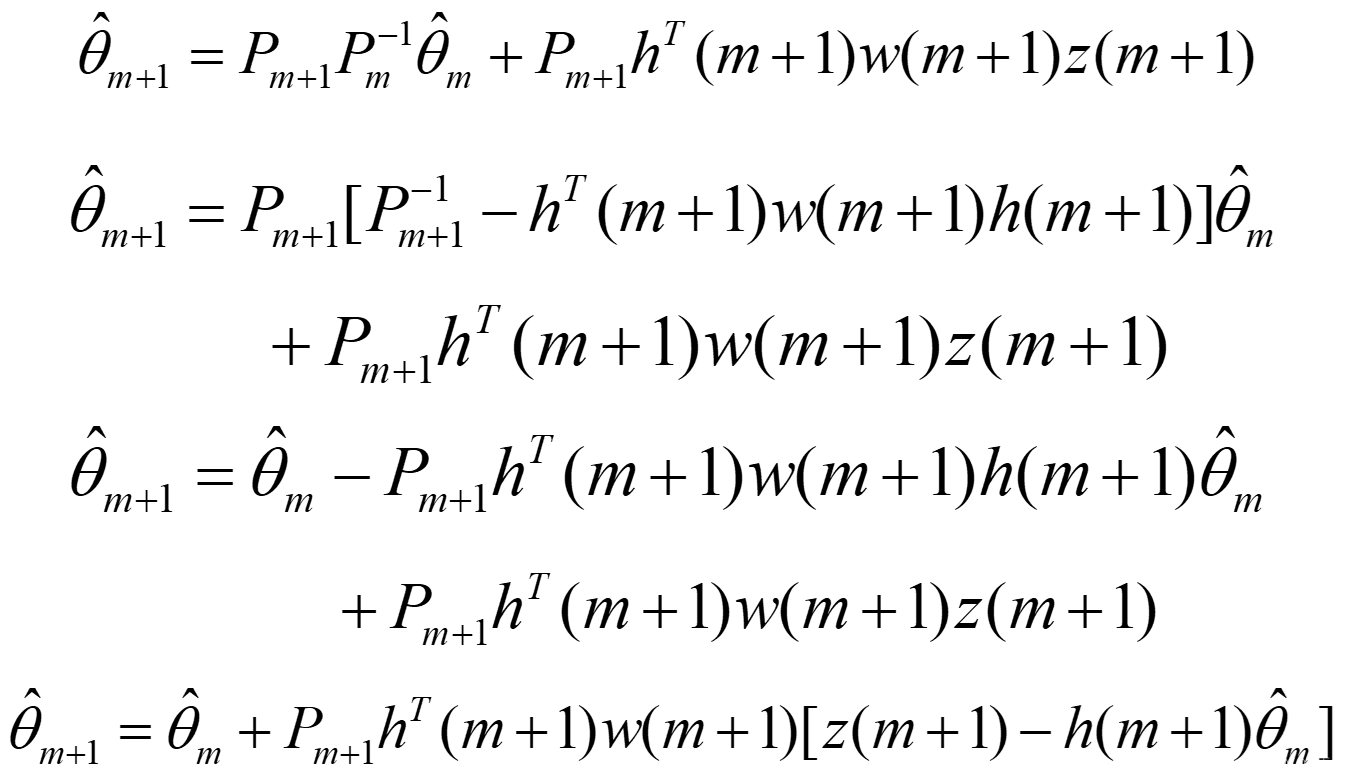
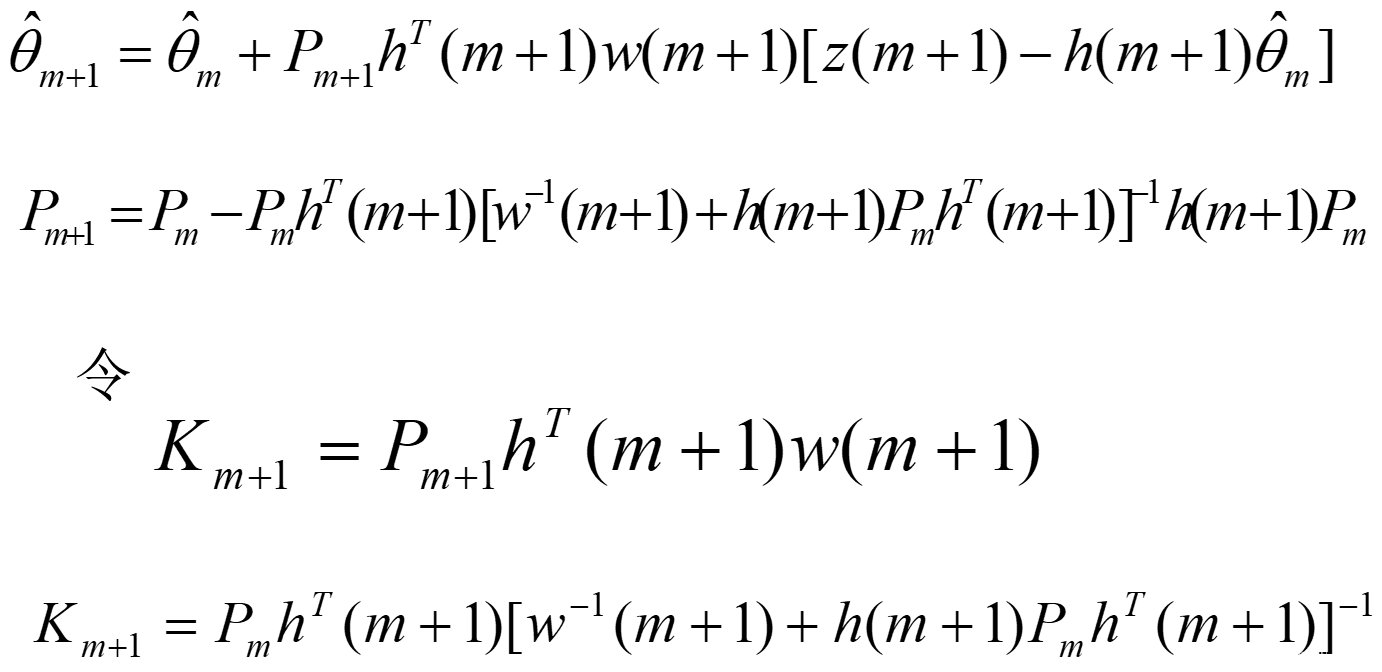

P ( m ) − P ( m + 1 ) ⩾ 0 P(m)-P(m+1)\geqslant0 P(m)−P(m+1)⩾0,随着递推次数的增加, P ( m ) P(m) P(m)和 K ( m ) K(m) K(m)逐渐减小,直至趋于0。数据饱和后,由于递推计算的舍入误差,不仅新的观测值对参数估计不起修正作用,反而使 P ( m ) P(m) P(m)失去正定性,导致估计误差增加。
当系统参数随时间变化时,因新数据被旧数据淹没,递推算法无法直接使用。为适应时变参数的情况,修改算法时旧数据的权重(降低),增加新数据的作用。
主要方法有数据窗法和Kalman滤波法。
四、增广最小二乘法
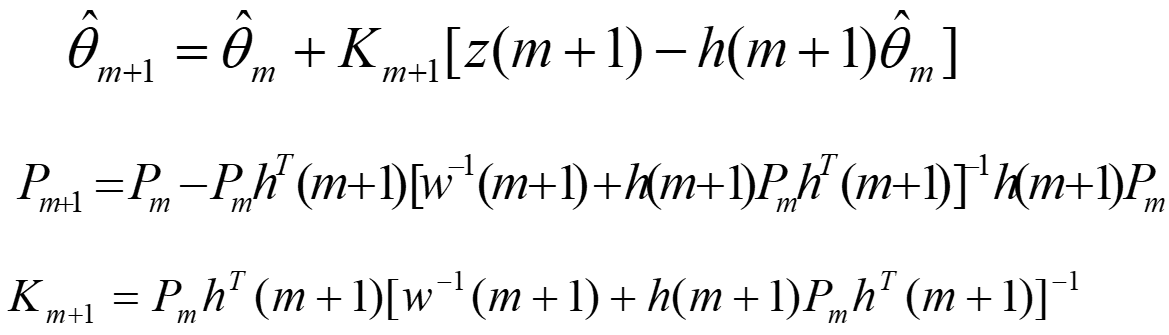
对比:
| 方法 | 优点 | 缺点 |
|---|---|---|
| 一般最小二乘法 | 白噪声可得无偏渐进无偏估计;算法简单可靠;计算量小;一次即可完成算法,适合离线辨识 | 当矩阵维度增加时,矩阵求逆运算会急剧增加,给计算机的运算速度和存储量带来负担 |
| 递推最小二乘法 | 可以减小数据存储量,避免矩阵求逆,减少计算量 | 会出现数据饱和现象 |
| 增广最小二乘法 | 将噪声模型的辨识同时考虑进去 | 当数据长度较大时,辨识精度低于极大似然法 |
参考:
[1]刘金琨,沈晓蓉,赵龙.系统辨识理论及MATLAB仿真[M].电子工业出版社,2013.
![[数据结构]—带头双向循环链表——超详解](http://pic.xiahunao.cn/[数据结构]—带头双向循环链表——超详解)

)

)














