【每日一题】—— C. Anonymous Informant（Codeforces Round 908 (Div. 2)）（思维题）

🌏博客主页：PH_modest的博客主页
🚩当前专栏：每日一题
💌其他专栏：
🔴 每日反刍
🟡 C++跬步积累
🟢 C语言跬步积累
🌈座右铭：广积粮，缓称王！

一.题目描述

在这里插入图片描述

题目大意：

在这里插入图片描述

题目链接：

C. Anonymous Informant（Codeforces Round 908 (Div. 2)）

二.思路分析

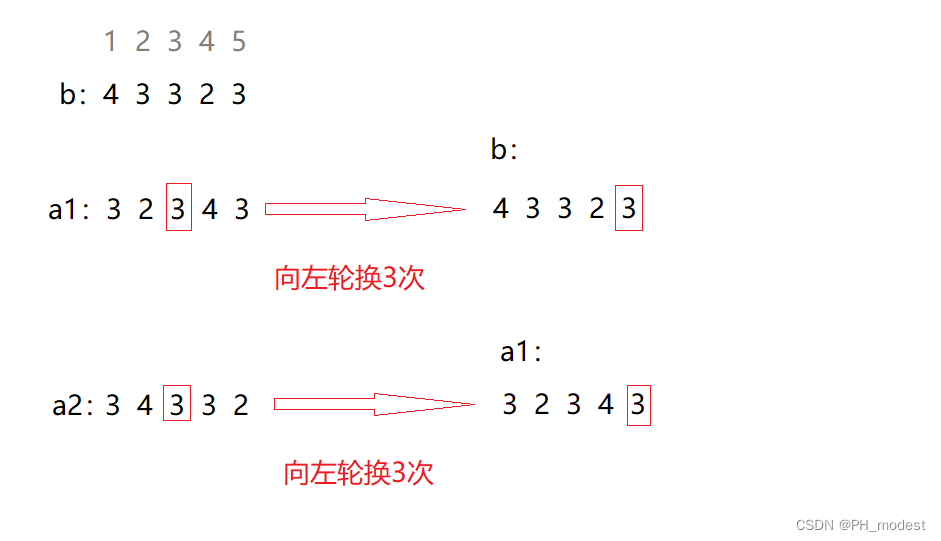
首先先理解题目，它是先给你一个数组b，b是由数组a通过轮换得到的，所以我们可以先通过b逆推前一个a：

①由此不难得出一个结论：当ai=i时，向左移动i次，那么ai一定位于该数组的最后一位；
②那么继续顺着这个思路往下走：也就说如果一个数组b可以通过数组a轮换得到，那么数组b的最后一位一定是数组a的ai=i的数，也就是说如果数组b的最后一个数大小在1~n之间，那么数组b就可以由a通过轮换得到；
③那么接下来就只需要先判断当前数组的最后一个数字是否满足条件，然后再将该数组逆推，得到上一个数组的最后一位，这边直接给结论：tmp=(tmp-s[tmp]+n)%n;，tmp是指最后一个数在数组b中的下标；
④最后就是优化问题了，因为k的大小是1e9，肯定会超时，而n是2e5，所以肯定需要根据数组长度进行优化：因为是按一个方向轮转，那么进行n次之后肯定会轮转回来，但又有一个问题，每次大轮转的轮转次数是不一定的（例如但a3=3时，我们轮转3次，当a2=2时，我们又只轮转2次，每个大轮转的次数和相加无法控制一定是n的倍数），我们无法控制，那么我们就可以找一个最坏的情况，也就是进行n个轮转次数，那么结果一定是n的倍数，那么我们只需要从n和k中取一个最小值即可： int cnt=min(k,n);

三.代码展示

//https://codeforces.com/contest/1894/problem/C
//
//
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;int s[200040];
void solve()
{int n,k;cin>>n>>k;for(int i=1;i<=n;i++){cin>>s[i];}int cnt=min(k,n);//没进行n次交换就会还原，但因为每次交换的次数不确定，所以最大的次数就是n次操作，这样无论每次操作多少次都是n的倍数int tmp=n;for(int i=0;i<cnt;i++){if(s[tmp]>n){cout<<"No"<<"\n";return;}else{
//			tmp+=n-s[tmp];//题解的写法，我不太能理解就换了一种写法tmp=(tmp-s[tmp]+n)%n;//下标的转换}}cout<<"Yes"<<"\n";
}signed main()
{int t;cin>>t;while(t--){solve();}return 0;
}