张量的生成
如何判断一个张量的维数:看张量的中括号有几层
0 1 2 :零维数列
[2 4 6] : 一维向量
[ [1 2 3] [4 5 6] ] : 二维数组 两行三列 第一行数据为 1 2 3 第二行数据为 4 5 6
以此类推 n维张量有n层中括号
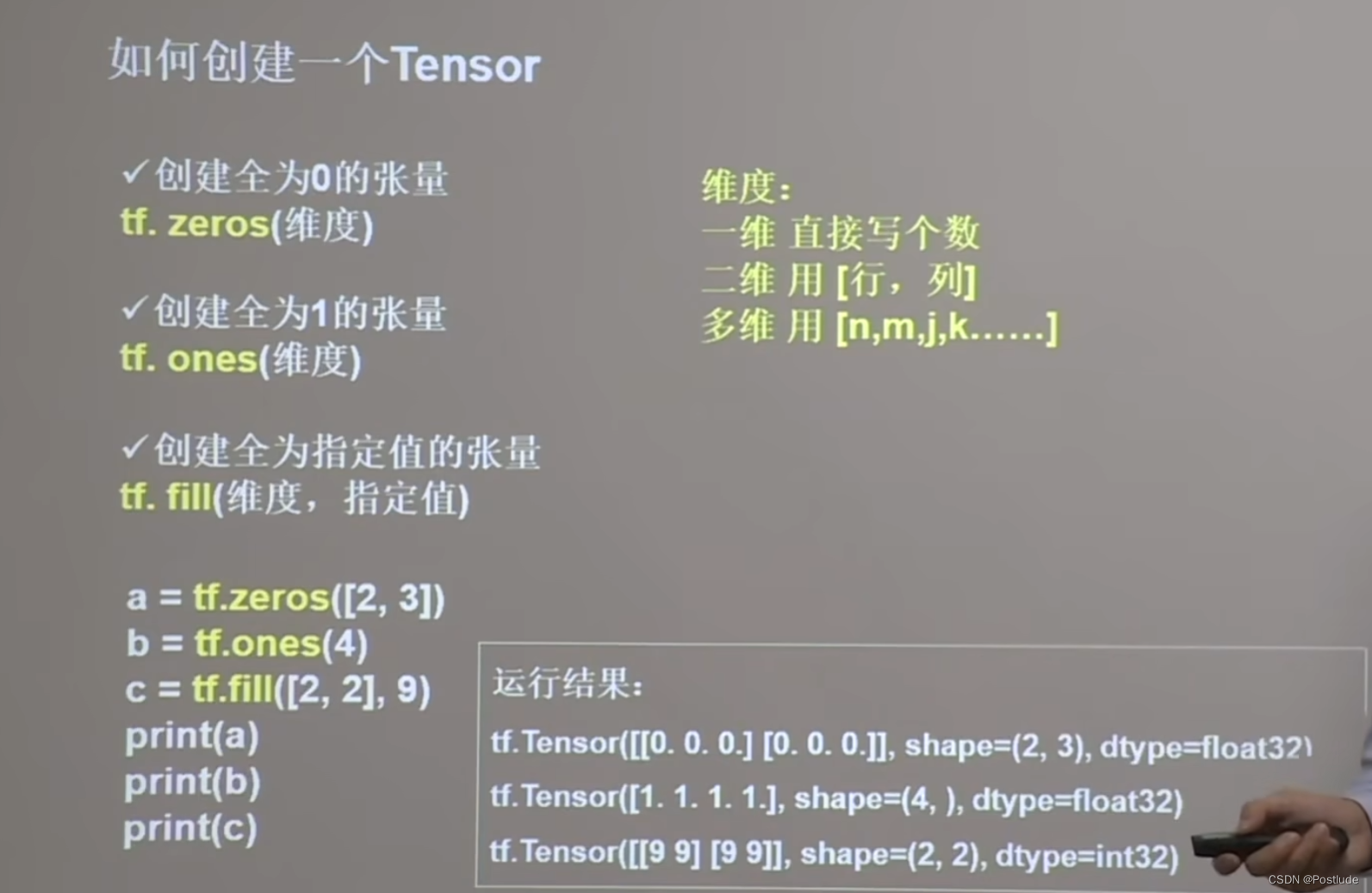
tf.zeros(%指定一个张量的维数%) 生成一个全0的张量
tf.ones(%指定一个张量的维数%) 生成一个全1的张量
tf.fill(%指定一个张量的维数%,%Value%) 生成一个全为Value的张量
随机张量的生成
在TF中,我们常常需要随机生成一个张量作为初始值 以下是常用函数
生成正态分布的随机值:
tf.random.normal(%维度%,mean=%均值(期望)%,stddev=%标准差%) 默认均值为0,标准差为1生成截断式的正态分布的随机值:
tf.random.truncated_normal(%维度%,mean=%均值(期望)%,stddev=%标准差% ) 默认均值为0,标准差为1
这种方式可以保证随机数在 (υ-2σ,υ+2σ)区间内 不至于太大或太小生成均匀分布的随机数:
tf.random.uniform(%维度%,minval=%最小值%,maxval=%最大值%) - 前闭后开区间
例:random=tf.random,uniform([2,2],minval=1,maxval=4)








(转载))










