接着Python机器学习算法入门教程(第二部分),继续展开描述。
十三、sklearn实现KNN分类算法
Pyhthon Sklearn 机器学习库提供了 neighbors 模块,该模块下提供了 KNN 算法的常用方法,如下所示:
| 类方法 | 说明 |
|---|---|
| KNeighborsClassifier | KNN 算法解决分类问题 |
| KNeighborsRegressor | KNN 算法解决回归问题 |
| RadiusNeighborsClassifier | 基于半径来查找最近邻的分类算法 |
| NearestNeighbors | 基于无监督学习实现KNN算法 |
| KDTree | 无监督学习下基于 KDTree 来查找最近邻的分类算法 |
| BallTree | 无监督学习下基于 BallTree 来查找最近邻的分类算法 |
本节可以通过调用 KNeighborsClassifier 实现 KNN 分类算法。下面对 Sklearn 自带的“红酒数据集”进行 KNN 算法分类预测。最终实现向训练好的模型喂入数据,输出相应的红酒类别,示例代码如下:
#加载红酒数据集
from sklearn.datasets import load_wine
#KNN分类算法
from sklearn.neighbors import KNeighborsClassifier
#分割训练集与测试集
from sklearn.model_selection import train_test_split
#导入numpy
import numpy as np
#加载数据集
wine_dataset=load_wine()
#查看数据集对应的键
print("红酒数据集的键:\n{}".format(wine_dataset.keys()))
print("数据集描述:\n{}".format(wine_dataset['data'].shape))# data 为数据集数据;target 为样本标签
#分割数据集,比例为 训练集:测试集 = 8:2
X_train,X_test,y_train,y_test=train_test_split(wine_dataset['data'],wine_dataset['target'],test_size=0.2,random_state=0)#构建knn分类模型,并指定 k 值
KNN=KNeighborsClassifier(n_neighbors=10)#使用训练集训练模型
KNN.fit(X_train,y_train)#评估模型的得分
score=KNN.score(X_test,y_test)
print(score)
#给出一组数据对酒进行分类
X_wine_test=np.array([[11.8,4.39,2.39,29,82,2.86,3.53,0.21,2.85,2.8,.75,3.78,490]])
predict_result=KNN.predict(X_wine_test)
print(predict_result)
print("分类结果:{}".format(wine_dataset['target_names'][predict_result]))输出结果:
红酒数据集的键:
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names'])
数据集描述: (178, 13) 0.75 [1]
分类结果:['class_1']
最终输入数据的预测结果为 1 类别。
十四、通俗地理解贝叶斯公式(定理)
朴素贝叶斯(Naive Bayesian algorithm)是有监督学习的一种分类算法,它基于“贝叶斯定理”实现,该原理的提出人是英国著名数学家托马斯·贝叶斯。贝叶斯定理是基于概率论和统计学的相关知识实现的,因此在正式学习“朴素贝叶斯算法”前,我们有必要先认识“贝叶斯定理”。
1、贝叶斯定理
贝叶斯定理的发明者 托马斯·贝叶斯 提出了一个很有意思的假设:“如果一个袋子中共有 10 个球,分别是黑球和白球,但是我们不知道它们之间的比例是怎么样的,现在,仅通过摸出的球的颜色,是否能判断出袋子里面黑白球的比例?”
上述问题可能与我们高中时期所接受的的概率有所冲突,因为你所接触的概率问题可能是这样的:“一个袋子里面有 10 个球,其中 4 个黑球,6 个白球,如果你随机抓取一个球,那么是黑球的概率是多少?”毫无疑问,答案是 0.4。这个问题非常简单,因为我们事先知道了袋子里面黑球和白球的比例,所以很容易算出摸一个球的概率,但是在某些复杂情况下,我们无法得知“比例”,此时就引出了贝叶斯提出的问题。
在统计学中有两个较大的分支:一个是“频率”,另一个便是“贝叶斯”,它们都有各自庞大的知识体系,而“贝叶斯”主要利用了“相关性”一词。下面以通俗易懂的方式描述一下“贝叶斯定理”:通常,事件 A 在事件 B 发生的条件下与事件 B 在事件 A 发生的条件下,它们两者的概率并不相同,但是它们两者之间存在一定的相关性,并具有以下公式(称之为“贝叶斯公式”):
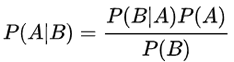
看到上述公式,你可能一头雾水,不过不必慌张,下面我们来了解一下“贝叶斯”公式。
(1)符号意义
首先我们要了解上述公式中符号的意义:
- P(A) 这是概率中最基本的符号,表示 A 出现的概率。比如在投掷骰子时,P(2) 指的是骰子出现数字“2”的概率,这个概率是 六分之一。
- P(B|A) 是条件概率的符号,表示事件 A 发生的条件下,事件 B 发生的概率,条件概率是“贝叶斯公式”的关键所在,它也被称为“似然度”。
- P(A|B) 是条件概率的符号,表示事件 B 发生的条件下,事件 A 发生的概率,这个计算结果也被称为“后验概率”。
有上述描述可知,贝叶斯公式可以预测事件发生的概率,两个本来相互独立的事件,发生了某种“相关性”,此时就可以通过“贝叶斯公式”实现预测。
2、条件概率
条件概率是“贝叶斯公式”的关键所在,那么如何理解条件概率呢?其实我们可以从“相关性”这一词语出发。举一个简单的例子,比如小明和小红是同班同学,他们各自准时回家的概率是 P(小明回家) = 1/2 和 P(小红回家) =1/2,但是假如小明和小红是好朋友,每天都会一起回家,那么 P(小红回家|小明回家) = 1 (理想状态下)。
上述示例就是条件概率的应用,小红和小明之间产生了某种关联性,本来俩个相互独立的事件,变得不再独立。但是还有一种情况,比如小亮每天准时到家 P(小亮回家) =1/2,但是小亮喜欢独来独往,如果问 P(小亮回家|小红回家) 的概率是多少呢?你会发现这两者之间不存在“相关性”,小红是否到家,不会影响小亮的概率结果,因此小亮准时到家的概率仍然是 1/2。
贝叶斯公式的核心是“条件概率”,譬如 P(B|A),就表示当 A 发生时,B 发生的概率,如果P(B|A)的值越大,说明一旦发生了 A,B 就越可能发生。两者可能存在较高的相关性。
3、先验概率
在贝叶斯看来,世界并非静止不动的,而是动态和相对的,他希望利用已知经验来进行判断,那么如何用经验进行判断呢?这里就必须要提到“先验”和“后验”这两个词语。我们先讲解“先验”,其实“先验”就相当于“未卜先知”,在事情即将发生之前,做一个概率预判。比如从远处驶来了一辆车,是轿车的概率是 45%,是货车的概率是 35%,是大客车的概率是 20%,在你没有看清之前基本靠猜,此时,我们把这个概率就叫做“先验概率”。
4、后验概率
在理解了“先验概率”的基础上,我们来研究一下什么是“后验概率?”
我们知道每一个事物都有自己的特征,比如前面所说的轿车、货车、客车,它们都有着各自不同的特征,距离过远的时候,我们无法用肉眼分辨,而当距离达到一定范围内就可以根据各自的特征再次做出概率预判,这就是后验概率。比如轿车的速度相比于另外两者更快可以记做 P(轿车|速度快) = 55%,而客车体型可能更大,可以记做 P(客车|体型大) = 35%。
如果用条件概率来表述 P(体型大|客车)=35%,这种通过“车辆类别”推算出“类别特征”发生的的概率的方法叫作“似然度”。这里的似然就是“可能性”的意思。
5、朴素+贝叶斯
了解完上述概念,你可能对贝叶斯定理有了一个基本的认识,实际上贝叶斯定理就是求解后验概率的过程,而核心方法是通过似然度预测后验概率,通过不断提高似然度,自然也就达到了提高后验概率的目的。
我们知道“朴素贝叶斯算法”由两个词语组成。朴素(native)是用来修饰“贝叶斯”这个名词的。按照中文的理解“朴素”意味着简单不奢华。朴素的英文是“native”,意味着“单纯天真”。
朴素贝叶斯是一种简单的贝叶斯算法,因为贝叶斯定理涉及到了概率学、统计学,其应用相对复杂,因此我们只能以简单的方式使用它,比如天真的认为,所有事物之间的特征都是相互独立的,彼此互不影响。关于朴素贝爷斯算法在下一节会详细介绍。
十五、朴素贝叶斯分类算法原理
在上面一节,我们基本认识了“贝叶斯定理”。在此基础之上,这一节我们将深入讲解“朴素贝叶斯算法”。
我们知道解决分类问题时,需要根据他们各自的特征来进行判断,比如区分“一对双胞胎不同之处”,虽然他们看起来相似,但是我们仍然可以根据细微的特征,来区分他们,并准确地叫出他们的名字。就像一句非常有哲理的话,“世界上没有完全相同的两片树叶”,因此被分类的事物会存在许多特征。
比如现在有 A1 和 A2 两个类,其中 A1 具有 b、c 两个特征,A2 具有 b、d 两个 特征,如果是你会怎么区分这两个类呢?很简单看看是存在 c ,存在的就是 A1,反之则是 A2。但是现实的情况要复杂的多,比如 100 个 A1样本中有 80% 的样本具有特征 c,而且剩余的 20% 具有了特征 d,那么要怎么对它们分类呢?其实只要多加判断还是可以分清,不过要是纯手工分类,那就恐怕得不偿失了。
1、多特征分类问题
统计学是通过搜索、整理、分析、描述数据等手段,以达到推断、预测对象的本质,统计学用到了大量的数学及其它学科的专业知识,其应用范围几乎覆盖了社会科学和自然科学的各个领域。
下面我们使统计学的相关知识解决上述分类问题,分类问题的样本数据大致如下所示:
[特征 X1 的值,特征 X2 的值,特征 X3 的值,......,类别 A1]
[特征 X1 的值,特征 X2 的值,特征 X3 的值,......,类别 A2]
解决思路:这里我们先简单的采用 1 和 0 代表特征值的有无,比如当 X1 的特征值等于 1 时,则该样本属于 A1 的类别概率;特征值 X2 值为 1 时,该样本属于类别 A1 的类别的概率。依次类推,然后最终算出该样本对于各个类别的概率值,哪个概率值最大就可能是哪个类。
上述思路就是贝叶斯定理的典型应用,如果使用条件概率表达,如下所示:
P(类别A1|特征X1,特征X2,特征X3,…)
上述式子表达的意思是:在特征 X1、X2、X3 等共同发生的条件下,类别 A1 发生的概率,也就是后验概率,依据贝叶斯公式,我们可以使用似然度求解后验概率,某个特征的似然度如下:
P(特征X1|类别A1,特征X2,特征X3,…)
但是要收集对个特征值共同发生的情况,这并不容易,因此我们就需要使用“朴素”贝叶斯算法。
2、朴素贝叶斯算法
上一节我们已经了解了贝叶斯公式,下面使用贝叶斯公式将多特征分类问题表达出来,如下所示:

数据集有时并不是很完全的,总会因为某些原因存在一些缺失和收集不全的现象,所以特征 x 越多这个问题就会越突出,统计这些特征出现的概率就越困难。为了避免这一问题,朴素贝叶斯算法做了一个假设,即特征之间相互独立,互不影响,由此以来,就可以简化为以下式子来求解某个特征的似然度:
![]()
“朴素贝叶斯算法”利用后验概率进行预测,其核心方法是通过似然度预测后验概率。在使用朴素贝叶斯算法解决分类问题,其实就是不断提高似然度的过程,你可以理解为后验概率正比于似然度,如果提高了似然度,那么也会达到提高后验概率的目的,记做如下式子:
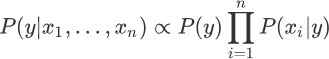
上述式子中∝表示正比于,而∏则是连乘符号(即概率相乘)表示了不同特征同时发生的概率。
3、朴素贝叶斯优化方法
你也许会发现,在学习过朴素贝叶斯的过程中,我们并未提到“假设函数”和“损失函数”,其实这并不难理解。朴素贝叶斯算法更像是一种统计方法,通过比较不同特征与类之间的似然度关系,最后把似然度最大的类作为预测结果。
每个类与特征的似然度是不同的,也就是 P(xi|y) 不同,因此某一类别中某个特征的概率越大,我们就更容易对该类别进行分类。根据求解后验概率的公式,可以得出以下优化方法:
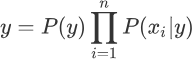
此时将后验概率记做类别 y,我们知道 P(y) 是一个固定的概率值,因此要想让 y 取得最大值,只能通过 P(xi|y) 实现,不妨把被统计的数据看成是一张大表格,朴素贝叶斯算法就是从中找到 P(xi|y) 值最大的那一项,该项对应的 y 是什么,则最终输出的预测结果就是什么。
十六、sklearn应用朴素贝叶斯算法
通过两节知识的学习,相信你对朴素贝叶斯算法有了初步的掌握,本节将实际应用朴素贝叶斯算法,从实战中体会算法的精妙之处。
首先看下面一个简单应用案例:
1、应用案例
假设一个学校有 45% 的男生和 55% 的女生,学校规定不能穿奇装异服,男生的裤子只能穿长筒裤,而女生可以穿裙子或者长筒裤,已知该学校穿长筒裤的女生和穿裙子的女生数量相等,所有男生都必须穿长筒裤,请问如果你从远处看到一个穿裤子的学生,那么这个学生是女生的概率是多少?
看完上述问题,你是不是已经很快的计算出了结果呢?还是丈二和尚,摸不到头脑呢?下面我们一起来分析一下,我们根据贝叶斯公式,列出要用到的事件概率:
学校女生的概率:P(女生)= 0.55
女生中穿裤子的概率:P(裤子|女)= 0.5
学校中穿裤子的概率:P(裤子)= 0.45 + 0.275= 0.725
知道了上述概率,下面使用贝叶斯公式求解 P(女生|裤子) 的概率:
P(女|裤子) = P(裤子|女生) * P(女生) / P(裤子) = 0.5 * 0.55 / 0.725 = 0.379
利用上述公式就计算除了后验概率 P(女生|裤子) 的概率,这里的 P(女生) 和 P(裤子)叫做先验概率,而 P(裤子|女生) 就是我们经常提起的条件概率“似然度”。
2、sklearn实现朴素贝叶斯
在 sklearn 库中,基于贝叶斯定理的算法集中在 sklearn.naive_bayes 包中,根据对“似然度 P(xi|y)”计算方法的不同,我们将朴素贝叶斯大致分为三种:多项式朴素贝叶斯(MultinomialNB)、伯努利分布朴素贝叶斯(BernoulliNB)、高斯分布朴素贝叶斯(GaussianNB)。另外一点要牢记,朴素贝叶斯算法的实现是基于假设而来,在朴素贝叶斯看来,特征之间是相互独立的,互不影响的。
高斯朴素贝叶斯适用于特征呈正态分布的,
多项式贝叶斯适用于特征是多项式分布的,
伯努利贝叶斯适用于二项分布。
(1)算法使用流程
使用朴素贝叶斯算法,具体分为三步:
- 统计样本数,即统计先验概率 P(y) 和 似然度 P(x|y)。
- 根据待测样本所包含的特征,对不同类分别进行后验概率计算。
- 比较 y1,y2,...yn 的后验概率,哪个的概率值最大就将其作为预测输出。
(2)朴素贝叶斯算法应用
下面通过鸢尾花数据集对朴素贝叶斯分类算法进行简单讲解。如下所示:
#鸢尾花数据集
from sklearn.datasets import load_iris
#导入朴素贝叶斯模型,这里选用高斯分类器
from sklearn.naive_bayes import GaussianNB#载入数据集
X,y=load_iris(return_X_y=True)
bayes_modle=GaussianNB()
#训练数据
bayes_modle.fit(X,y)
#使用模型进行分类预测
result=bayes_modle.predict(X)
print(result)
#对模型评分model_score=bayes_modle.score(X,y)
print(model_score)输出结果:
预测分类:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1
1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 2 2 2 2
2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
模型评分:
0.96
十七、决策树分类算法(if-else原理)
在本节我们将介绍“机器学习”中的“明星”算法“决策树算法”。决策树算法在“决策”领域有着广泛的应用,比如个人决策、公司管理决策等。其实更准确的来讲,决策树算法算是一类算法,这类算法逻辑模型以“树形结构”呈现,因此它比较容易理解,并不是很复杂,我们可以清楚的掌握分类过程中的每一个细节。
1、if-else原理
想要认识“决策树算法”我们不妨从最简单的“if - else原理”出发来一探究竟。作为程序员,我相信你对 if -else 原理并不感到陌生,它是条件判断的常用语句。下面简单描述一下 if -else 的用法:if 后跟判断条件,如果判断为真,也即满足条件,就执行 if 下的代码段,否则执行 else 下的代码段,因此 if-else 可以简单的理解为“如果满足条件就....,否则.....”
if-else 有两个特性:一是能够利用 if -else 进行条件判断,但需要首先给出判断条件;二是能无限嵌套,也就是在一个 if-else 的条件执行体中,能够再嵌套另外一个 if-else,从而实现无限循环嵌套。
下面我看一个简单的应用示例,相信你能从中体会到“决策树”的魅力。古人有“伯乐识别千里马”那么“伯乐”是如何“相马”的呢?下表列出了 A、B、C 、D 四匹马,它们具有以下特征:
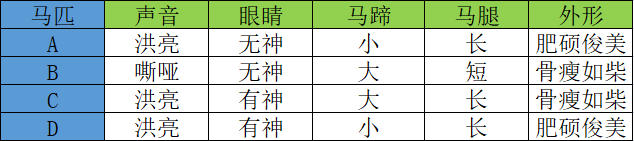
如果你是“伯乐”会如何从中挑选出那匹“千里马”呢?毫无疑问,我们要根据马匹的相应特征去判断,而这些特征对应的值叫做“特征维度值”,下面是一位“伯乐”利用 if -else 原理,最终成功的审识别出“千里马”的全过程,如下所示:
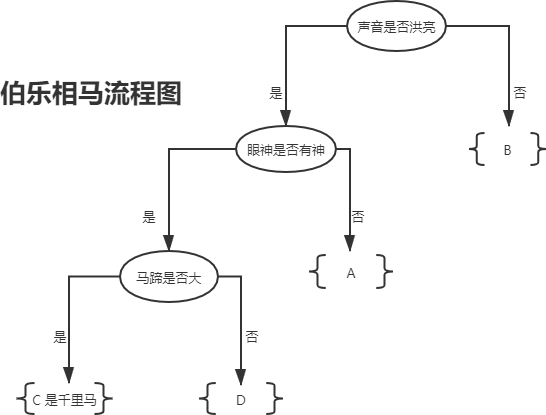
图1:决策树流程图
上图 1 所示是一颗典型的树形结构“二叉树”,而决策树一词中的“树”指的就是这棵树。上图展示了伯乐“识别”千里马的全过程,根据特征值的有无(if-else原理)最终找出“千里马。你可能会问为什么并没囊括所有的特征值?
这是因为某些特征值对于结果的判断而言,并不是最为关键的特征值,比如马的“体型”,“骨瘦如柴”并不能决定某一匹马不是“千里马”。而“马腿”的长短没有作为判断条件,这是因为使用前三个特征值就已经完成了结果的分类,如果此时再使用“马腿”长短作为判断条件,则有点多此一举。
如果将上述判断的流程用 if-else 的伪代码写出来,如下所示:
if (特征值"声音"为"是"):
if(特征值"眼睛有神"为"是"):
if (特征值"马蹄大"为"是"):
类别千里马 C
else:
类别普通马匹 D
else:
类别普通马匹 A
else:
类别普通马匹 B
2、决策树算法关键
了解了“if-else”原理,下面我们进一步认识决策树算法。决策树算法涉及了几个重要的知识点:“决策树的分类方法”,“分支节点划分问题”以及“纯度的概念”。当然在学习过程中还会涉及到“信息熵”、“信息增益”、“基尼指数”的概念,相关知识在后面会逐一介绍。
(1)特征维度&判别条件
我们知道分类问题的数据集由许多样本构成,而每个样本数据又会有多个特征维度,比如前面例子中马的“声音”,“眼睛”都属于特征维度,在决策算法中这些特征维度属于一个集合,称为“特征维度集”。数据样本的特征维度与最终样本的分类都可能存在着某种关联,因此决策树的判别条件将从特征维度集中产生。
在机器学习中,决策树算法是一种有监督的分类算法,我们知道机器学习其实主要完成两件事,一个是模型的训练与测试,另外一个是预测数据的(分类问题,预测类别),因此对于决策树算法而言,我们要考虑如何学会自动选择最合适的判别条件,如图 1 所示,只利用前三个特征就完成了分类的预测。这也将是接下来要探讨的重要问题。
十八、决策树算法:选择决策条件
首先来看一个“我想你来猜”的游戏,游戏规则很简单:一个人从脑海中构建一个事物,另外几个人最多可以向他提问 20 个问题,游戏规定,问题的答案只能用是或者否来回答。问问题的人通过回答者的“答案”来推分析、逐步缩小待猜测事物的范围,从而来判断他想的是什么。其实这个游戏与决策树工作过程相似。
那么你有没有考虑过要怎样选择“问什么问题”呢,在这里“问什么问题”就相当于决策树算法中的“判别条件”。选择什么判别条件,可以让我们又快又准确的实现分类,这是本节介绍的重点知识。
1、纯度的概念
决策树算法引入了“纯度”的概念,“纯”指的是单一,而“度”则指的是“度量”。“纯度”是对单一类样本在子集内所占重的的度量。
在每一次判别结束后,如果集合中归属于同一类别的样本越多,那么就说明这个集合的纯度就越高。比如,二元分类问题的数据集都会被分成两个子集,我们通过自己的纯度就可以判断分类效果的好与坏,子集的纯度越高,就说明分类效果越好。
上一节我们提到过,决策树算法是一类算法,并非某一种算法,其中最著名的决策树算法有三种,分别是 ID3、C4.5 和 CART。虽然他们都属于决策树算法,不过它们之间也存在着一些细微的差别,主要是体现在衡量“纯度”的方法上,它们分别采用了信息增益、增益率和基尼指数,这些算法的相关概念将在后续内容为大家说明。
2、纯度度量规则
那么我们应该采取什么样的方法去“衡量”某个集合中某一类别样本的纯度呢?当我们学习完机器学习之后,我们总不能还使用人工的方式去验证吧,那可真是徒劳无功了。
要想明确纯度的衡量方法,首先我们要知道一些度量“纯度”的规则。下面我们将类别分为“正类与负类”,如下所示:
- 某个分支节点下所有样本都属于同一个类别,纯度达到最高值。
- 某个分支节点下样本所属的类别一半是正类一半是负类,此时,纯度取得最低值。
- 纯度代表一个类在子集中的占比多少,它并不在乎该类究竟是正类还是负类。比如,某个分支下不管是正类占比 60% 还是负类占比 60%,其纯度的度量值都是一样的。
决策树算法中使用了大量的二叉树进行判别,在一次判别后,最理想的情况是分支节点下包含的类完全相同,也就是说不同的类别完全分开,但有时我们无法只用一个判别条件就让不同的类之间完全分开,因此选择合适判别条件区划分类是我们要重点掌握的。
3、纯度度量方法
根据之前学习的机器学习算法,如果要求得子集内某一类别所占比最大或者最小,就需要使用求极值的方法。因此,接下来探讨使得纯度能够达到最大值和最小值的“纯度函数”。
(1) 纯度函数
现在我们做一个函数图像,横轴表示某个类的占比,纵轴表示纯度值,然后我们根据上面提出的“纯度度量规则”来绘制函数图像:
首先某个类达到最大值,或者最小值时,纯度达到最高值,然后,当某一个类的占比达到 0.5 时,纯度将取得最低值。由这两个条件,我们可以做出 a/b/c 三个点,最后用一条平滑的曲线将这三个点连接起来。如下所示:
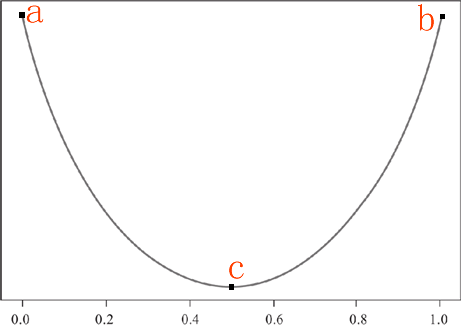
图1:纯度函数图像
如上图,我们做出了一条类似于抛物线的图像,你可以把它看做成“椭圆”的下半部分。当在 a 点时某一类的占比纯度最小,但是对于二元分类来说,一个类小,另一个类就会高,因此 a 点时的纯度也最高(与 b 恰好相反),当某类的纯度占比在 c 点时,对于二元分类来说,两个类占比相同,此时的纯度值最低,此时通过 c 点无法判断一个子集的所属类别。
(2) 纯度度量函数
前面在学习线性回归算法时,我们学习了损失函数,它的目的是用来计算损失值,从而调整参数值,使其预测值不断逼近于误差最小,而纯度度量函数的要求正好与纯度函数的要求相反,因为纯度值越低意味着损失值越高,反之则越低。所以纯度度量函数所作出来的图像与纯度函数正好相反。如下图所示:
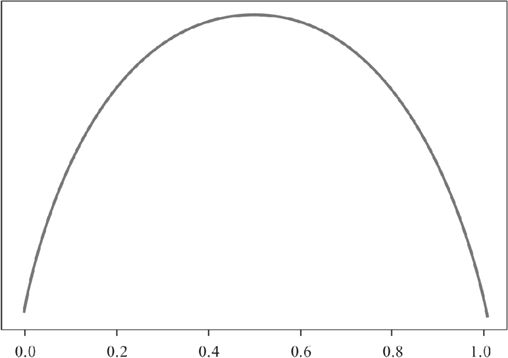
图2:纯度度量函数
上图就是纯度度量函数,它与纯度函数恰好相反。纯度度量函数图像适应于所有决策树算法,比如 ID3、C4.5、CART 等经典算法。
下一部分将在Python机器学习算法入门教程(第四部分)展开描述。

》重磅发布)















![[pytorch]手动构建一个神经网络并且训练](http://pic.xiahunao.cn/[pytorch]手动构建一个神经网络并且训练)
`flash_eraseall` 擦除整个Flash存储器)
