目录

树结构及其算法-二叉树节点的插入

C++代码

---

树结构及其算法-二叉树节点的插入

二叉树节点插入的情况和查找相似，重点是插入后仍要保持二叉查找树的特性。如果插入的节点已经在二叉树中，就没有插入的必要了，如果插入的值不在二叉树中，就会出现查找失败的情况，相当于找到了要插入的位置。

	if ((tree->Find(tree->GetTreeNode(), value)) != nullptr)cout << "二叉树中有此节点了" << endl;elsetree->AddNodeToTree(&value,	1);

C++代码

#include<iostream>
using namespace std;struct TreeNode {int data;TreeNode* leftNode;TreeNode* rightNode;TreeNode(int tempData, TreeNode* tempLeftNode = nullptr, TreeNode* tempRightNode = nullptr) {this->data = tempData;this->leftNode = tempLeftNode;this->rightNode = tempRightNode;}
};class Tree {
private:TreeNode* treeNode;
public:Tree() {treeNode = nullptr;}TreeNode* GetTreeNode() {return this->treeNode;}void AddNodeToTree(int* tempData, int tempSize) {for (int i = 0; i < tempSize; i++) {TreeNode* currentNode;TreeNode* newNode;int flag = 0;newNode = new TreeNode(tempData[i]);if (treeNode == nullptr)treeNode = newNode;else {currentNode = treeNode;while (!flag) {if (tempData[i] < currentNode->data) {if (currentNode->leftNode == nullptr) {currentNode->leftNode = newNode;flag = 1;}elsecurrentNode = currentNode->leftNode;}else {if (currentNode->rightNode == nullptr) {currentNode->rightNode = newNode;flag = 1;}elsecurrentNode = currentNode->rightNode;}}}}}void Inorder(TreeNode* tempTree) {if (tempTree != nullptr) {Inorder(tempTree->leftNode);cout << tempTree->data << " ";Inorder(tempTree->rightNode);}}TreeNode* Find(TreeNode* tree, int value) {while (true) {if (tree == nullptr)return nullptr;if (tree->data == value)return tree;else if (tree->data > value)tree = tree->leftNode;elsetree = tree->rightNode;}}
};int main() {int data[]{ 7,4,1,5,16,8,11,12,15,9,2 };cout << "原始数据：" << endl;for (int i = 0; i < 11; i++)cout << data[i] << " ";cout << endl;Tree* tree = new Tree;tree->AddNodeToTree(data, 11);cout << "中序遍历：" << endl;tree->Inorder(tree->GetTreeNode());cout << endl;cout << "请输入要插入的值：";int value;cin >> value;if ((tree->Find(tree->GetTreeNode(), value)) != nullptr)cout << "二叉树中有此节点了" << endl;else{tree->AddNodeToTree(&value,	1);cout << "中序遍历：" << endl;tree->Inorder(tree->GetTreeNode());cout << endl;}return 0;
}

输出结果
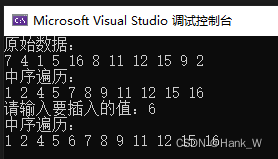