经典文献阅读之--DLIO(基于连续时间运动校正的轻量级激光雷达惯性导航系统)

0. 简介

一般来说，当系统经过不规则的地形时候，机器人自身会存在激烈运动会导致激光雷达扫描中的运动畸变，从而可能降低状态估计和建图的精度。虽然已经有一些方法用于缓解这种影响，但它们仍然过于简单或计算成本过高，难以应用于资源受限的移动机器人。之前这个团队开发了《经典文献阅读之–DLO》这套方法。该团队在23年又提出了《Direct LiDAR-Inertial Odometry: Lightweight LIO with Continuous-Time Motion Correction》一文。该轻量级激光雷达惯性导航系统算法，采用一种新的粗到细的方法构建连续时间轨迹以进行精确的运动校正。该方法的关键在于构建一组仅由时间参数化的解析方程，使得逐点去畸变的过程可以快速且可并行化。这种方法之所以可行，是因为我们的非线性几何观察器具有强大的收敛性质，可以为IMU的敏感积分步骤提供可靠的状态估计初始化。相关代码可以在GIthub上找到。

在这里插入图片描述

1. 主要贡献

本文提出了一种名为Direct LiDAR-Inertial Odometry (DLIO)的快速可靠的里程计算法，它提供了精确的定位和详细的三维建图（见图1），具有四个主要贡献。

首先，我们提出了一种新的粗到细的技术，用于构建连续时间轨迹，其中导出了一组具有恒定加加速度和角加速度运动模型的解析方程，以进行快速和可并行化的逐点运动校正。
其次，提出了一种新的简化结构，将运动校正和先验构建合并为一步，并直接执行扫描到地图的配准，大大降低了算法的总体计算负载。（Point-LIO也在做这个工作）
第三，我们利用了一种新的非线性几何观察器[10]，它具有强大的性能保证，对于实现前两个贡献至关重要，在管道中以最小的计算复杂度鲁棒地生成机器人完整状态的准确估计。
最后，我们通过使用多个数据集对最先进的技术进行广泛的实验验证，证明了我们方法的有效性。

2. 系统概述

DLIO是一种轻量级的LIO算法，通过一个包含两个主要组件和三个创新的独特架构生成机器人状态估计和几何地图（见图2）。第一个组件是一个快速的扫描匹配器，通过与提取的局部子地图进行对齐，将密集的、经过运动校正的点云注册到机器人的地图上。在 $W$ 中逐点进行连续时间积分，确保修正后的点云具有最大的图像保真度，同时为GICP优化建立先验。在第二个组件中，一个非线性几何观察器[10]使用第一个组件的姿态输出更新系统状态，提供高速和可靠的姿态、速度和传感器偏差估计，这些估计具有全局收敛性。然后，这些估计将初始化下一个运动校正、扫描匹配和状态更新的迭代。

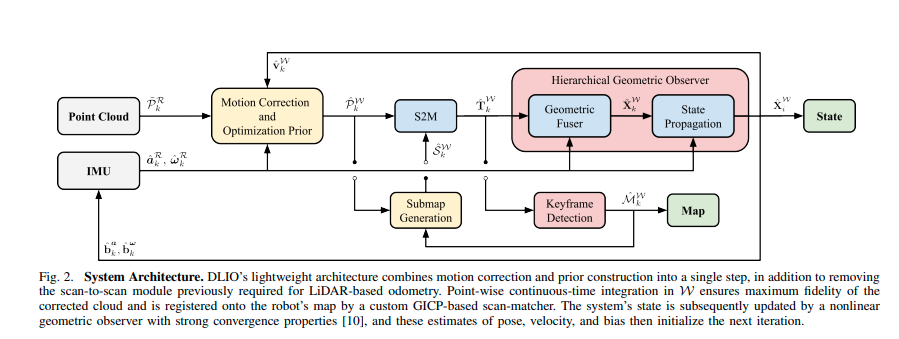
在这里插入图片描述

图2. 系统架构。DLIO的轻量级架构将运动校正和先验构建合并为一步，并去除了以前用于基于激光雷达的里程计所需的扫描对扫描模块。在W中逐点进行连续时间积分，确保修正后的点云具有最大的保真度，并通过自定义的基于GICP的扫描匹配器注册到机器人的地图上。随后，系统的状态由一个具有强大收敛性质的非线性几何观察器[10]进行更新，这些姿态、速度和偏差的估计然后初始化下一次迭代。

3. 符号表示

假设在时间 $t_k$ 开始的单次激光雷达扫描的点云表示为 $P_k$ ，并用 $k$ 进行索引。点云 $P_k$ 由相对于扫描开始时间的时间差 $∆t^n_k$ 测量的点 $p^n_k∈\mathbb{R}^3$ 组成，其中 $n = 1 ， \dots ， N$ ， $N$ 是扫描中的总点数。世界坐标系表示为 $W$ ，机器人坐标系表示为 $R$ ，位于其重心，其中 $x$ 指向前方， $y$ 指向左侧， $z$ 指向上方。IMU的坐标系表示为 $B$ ，激光雷达的坐标系表示为 $L$ ，机器人在索引 $k$ 处的状态向量 $X_k$ 定义为元组。

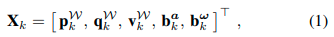
在这里插入图片描述

其中 $p^W ∈ \mathbb{R}^3$ 是机器人的位置， $q^W$ 是四元数编码的方向，采用Hamilton符号表示，位于 $\mathbb{S}^3$ ， $v^W ∈\mathbb{R}^3$ 是机器人的速度， $b^a ∈ \mathbb{R}^3$ 是加速度计的偏差， $b^ω ∈ \mathbb{R}^3$ 是陀螺仪的偏差。IMU的测量值 $\hat{a}$ 和 $\hat{ω}$ 被建模为

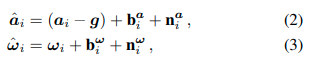
在这里插入图片描述

并用 $i = 1 ， \dots ， M$ 进行索引，表示在时钟时间 $t_{k-1}$ 和 $t_k$ 之间的 $M$ 次测量。为了简单起见，除非另有说明，否则索引 $k$ 和 $i$ 分别出现在激光雷达和IMU速率上，并以这种方式书写。原始传感器测量值 $a_i$ 和 $ω_i$ 包含偏差 $b_i$ 和白噪声 $n_i$ ， $g$ 是旋转后的重力向量。在本文中，我们解决以下问题：给定来自激光雷达的累积点云 $P_k$ 和由IMU在接收到每个扫描之间采样的测量值 $a_i$ **和 ** $ω_i$ ，估计机器人的状态 $\hat{X}^W_i$ 和几何地图 $\hat{M}^W_k$ 。

4. 预处理

DLIO的输入是由360度机械LiDAR（如Ouster或Velodyne（10-20Hz））收集的稠密的3D点云，以及来自6轴IMU的时间同步的线性加速度和角速度测量，IMU速率要比雷达高得多（100-500Hz）。在下游任务之前，所有传感器数据都通过外部校准转换为位于机器人重心处的 $R$ 。对于IMU，必须考虑将刚体上的线性加速度测量位移的影响，如果该传感器与重心不重合，则通过考虑所有线性加速度在 $R$ 处通过角速度和IMU偏移之间的叉积来完成。为了最小化信息丢失，除了在原点周围使用 $1m^3$ 的框滤波器以删除可能来自机器人本身的点，并使用轻量级体素滤波器进行更高分辨率的点云处理外，我们不对点云进行预处理。这使我们的工作与其他试图检测特征（例如角落、边缘或surfels）或通过体素滤波器大量下采样云的工作区分开来。

5. 带联合先验的连续时间运动校正(重点内容)

旋转LiDAR传感器收集的点云在移动过程中会因旋转激光阵列在扫描过程中的不同时刻收集点而受到运动失真的影响。我们不再假设简单的运动（例如，恒定速度）来捕捉精细的运动，而是使用更准确的恒定加速度和角加速度模型通过两步粗到细的传播方案为每个点计算唯一的变换。此策略旨在最小化由于IMU的采样率和IMU与LiDAR点测量之间的时间偏移而引起的误差。在W中通过数值IMU积分[29]首先粗略构建扫描的轨迹，随后通过解决一组解析连续时间方程来进行细化（图3）。

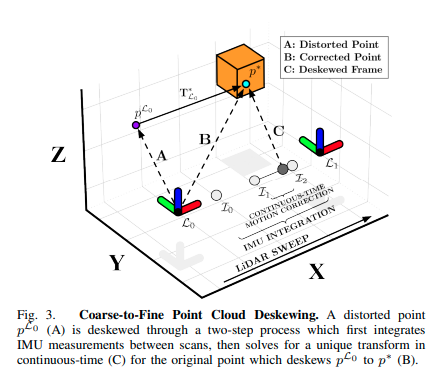
在这里插入图片描述

图3. 粗到细的点云去畸变。通过两步过程去畸变扭曲的点 $p^{L_0}(A)$ ，首先在扫描之间积分IMU测量，然后在连续时间中求解独特的变换（C）以将原始点 $p^{L_0}$ 去畸变为 $p^∗$ （B）

假设 $t_k$ 是接收到具有 $N$ 个累积点的点云 $P^R_k$ 的时钟时间，并且 $t_k + ∆t^n_k$ 是云中点 $p^n_k$ 的时间戳。为了近似每个点在 $W$ 中的位置，我们首先通过在 $t_{k-1}$ 和 $t_k + ∆t^N_k$ 之间积分IMU测量来获得运动估计：

对于 $i = 1 ， \dots ， M$ ，其中 $M$ 是两个扫描之间IMU测量的数量，其中 $\hat{j}_i = \frac{1}{∆t_i}(\hat{R}(\hat{q}_i)\hat{a}_i - \hat{R}(\hat{q}_{i-1})\hat{a}_{i-1})$ ， $\hat{α}_i = \frac{1}{∆t_i}(\hat{ω}_i - \hat{ω}_{i-1})$ 分别是估计的线性jerk和角加速度。与 $\hat{p}_i$ 和 $\hat{q}_i$ 相对应的一组齐次变换 $\hat{T}^W_i∈\mathbb{SE}（3）$ 然后定义了扫描期间粗略的离散时间轨迹。然后，从最近的前置变换到每个点 $p^n_k$ 的解析连续时间解决方案恢复特定于点的去畸变变换 $\hat{T}^{W∗}_n$ ，使得

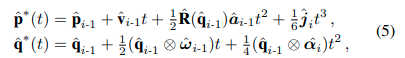
在这里插入图片描述

其中， $i - 1$ 和 $i$ 分别对应于最近的前一个和后一个IMU测量， $t$ 是点 $p^n_k$ 和最近的前一个IMU之间的时间戳， $\hat{T}^{W∗}_n$ 是对于 $p^n_k$ 所对应的 $p^∗$ 和 $q^∗$ 的变换（图4）。请注意，（5）仅由 $t$ 参数化，因此可以查询任何所需时间的变换以构建连续时间轨迹。