二叉搜索树的最小绝对差[简单]

优质博文：IT-BLOG-CN

一、题目

给你一个二叉搜索树的根节点root，返回树中任意两不同节点值之间的最小差值。差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

输入：root = [4,2,6,1,3]
输出：1

示例 2：

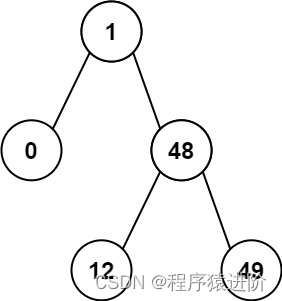
输入：root = [1,0,48,null,null,12,49]
输出：1

树中节点的数目范围是[2, 104]
0 <= Node.val <= 105

二、代码

考虑对升序数组a求任意两个元素之差的绝对值的最小值，答案一定为相邻两个元素之差的最小值，本题要求二叉搜索树任意两节点差的绝对值的最小值，而我们知道二叉搜索树有个性质为二叉搜索树中序遍历得到的值序列是递增有序的，因此我们只要得到中序遍历后的值序列就可以在中序遍历的过程中用pre变量保存前驱节点的值，这样即能边遍历边更新答案，不再需要显式创建数组来保存，需要注意的是pre的初始值需要设置成任意负数标记开头，下文代码中设置为−1

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {int minVal;// 定义临时变量，存储相邻节点，因为val都是正整数，所以使用-1表示第一次存储int pre;public int getMinimumDifference(TreeNode root) {// 定义一个最小值，不断的迭代进行判断minVal = Integer.MAX_VALUE;pre = -1;dfs(root);return minVal;}private void dfs(TreeNode root) {// 递归退出条件if (root == null) {return;}// 中序遍历数据，先遍历左子树dfs(root.left);if (pre == -1) {pre = root.val;} else {// 因为是从小到大顺序遍历，所以无需绝对值minVal = Math.min(minVal, root.val - pre);pre = root.val;}dfs(root.right);}
}