前言：
首先介绍一下算法(Algorithm)
算法是对特定问题求解步骤的一种描述。一个“好”的算法应该达到以下目标：正确性、可读性、健壮性、高效率与低存储量需求
算法的效率的度量 是通过 时间复杂度 和 空间复杂度 来描述的
一、时间复杂度
时间复杂度是指算法所需计算的时间量，通常用大 O 记号表示。它是衡量算法运行效率的一种指标。时间复杂度反映了当输入规模变大时，算法运行时间的增长趋势。
算法中的基本操作的执行次数，为算法的时间复杂度。
一般情况下，我们关注算法的最坏时间复杂度。最坏时间复杂度表示在算法最差情况下，算法所需计算的时间量。如果算法的最坏时间复杂度为 O(n)，则算法的时间复杂度为线性，表示算法的运行时间与输入规模 n 成正比。如果算法的最坏时间复杂度为 O(n^2)，则算法的时间复杂度为平方级别，表示算法的运行时间与输入规模 n 的平方成正比。
除了最坏时间复杂度，还有平均时间复杂度和最好时间复杂度等。不同的算法在不同的场景下，时间复杂度的表现也不同。
时间复杂度越小效率越高
常见的一些时间复杂度的例子：
例1：时间复杂度为O(N)
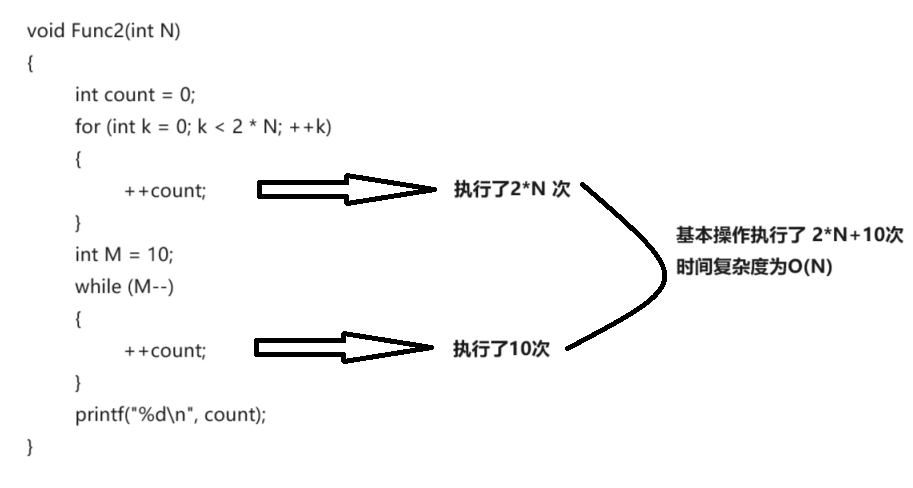
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
例2：
// 计算Func3的时间复杂度？
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
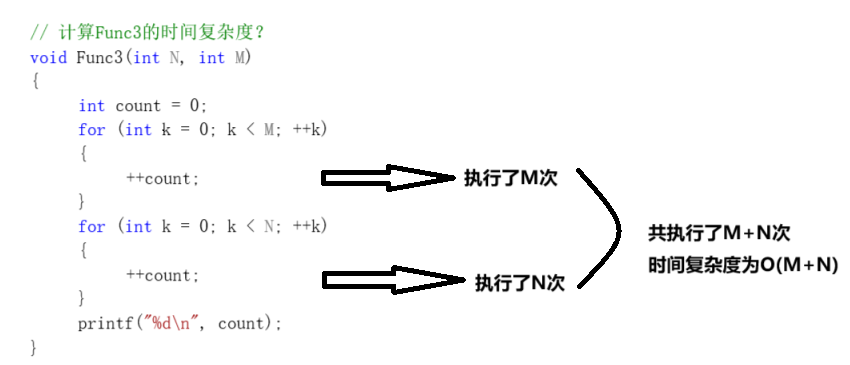
时间复杂度为 O(N+M)
例3：
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}基本操作执行了100次，故时间复杂度为：O(1)
例4：
提示：计算时间复杂度看的是思想
//计算下方代码的时间复杂度
const char * strchr ( const char * str, int character );strchr这个库函数作用是 在字符串中查找字串。最好的情况下查找一次就找到，最坏的情况下是查找完没有找到。
基本操作执行最好1次，最坏N次，时间复杂度一般看最坏，时间复杂度为 O(N)
例5：
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}计算时间复杂度主要看代码中的思想。冒泡排序
基本操作执行最好N次，最坏执行了(N*(N+1)/2次
时间复杂度为 O(N^2)
例6：
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]：begin和end是左闭右闭区间，因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}二分法，每次查找范围缩小一半，
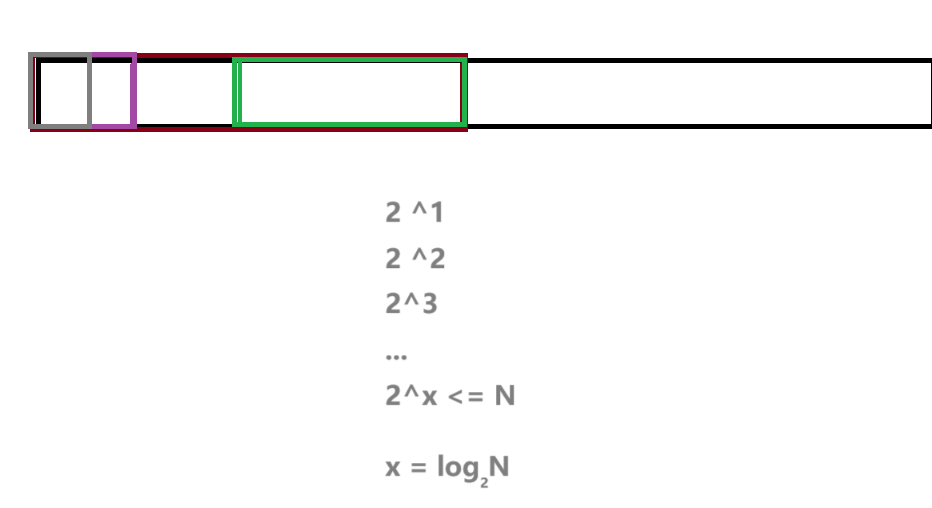
平时也可以写成 logN ,时间复杂度为 O(logN)
例7：计算递归的时间复杂度
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}这里只有N == 0 时返回 1 ，递归从 N 到 0，一个递归 N+1次 时间复杂度: O(N)
例8：
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}这里的递归，斐波那契数列，可以比作细胞分裂，每一个可以分出2个
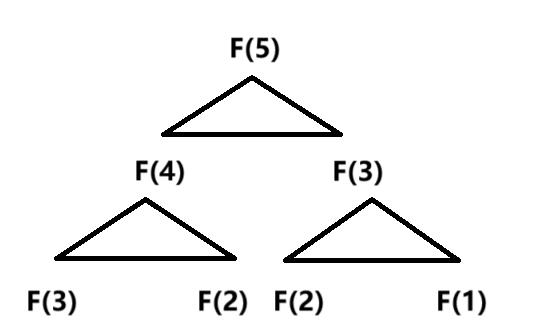
2^1 + 2^2 + ...+2^n == 2^n - 1
时间复杂度为：O(2^N)
例9：该题来自leetcoded 轮转数组
给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数
代码1
void rotate(int* nums, int numsSize, int k){int t = 0,i = 0;k%=numsSize;while(k--){t = nums[numsSize-1];for(i = 0;i<numsSize-1;i++){nums[numsSize-1-i] = nums[numsSize-i-2];}nums[0] = t;}}注意此代码提交过不了，原因是超时 ，题目解析 ：题解
当在好的情况下数组本身，右旋一个数组的时间复杂度就是O(N)，因为把最右边的元素拿出来，然后后移N - 1个元素，之后把拿出来的元素放到最左边。这就完成了一个元素的右旋。
当右旋两个元素的时候 基本操作执行了2*(N-1) 次
最坏情况右旋N-1 个元素，每右旋一个元素执行N次，进而算出 (N - 1)*N次
时间复杂度一般看最坏情况 ，O(N^2)
二、空间复杂度
空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
常见的空间复杂度的例子
计算下方代码的空间复杂度
例1：
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}空间复杂度 O(1)
例2：
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}空间复杂度：O(N)
例3：
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)
例4：
int ret(int* nums,int n)
{int arr[3][2];for (int i = 0; i < 3;i++){for (int j = 0; j < 2;j++){arr[i][j] = i+j;}}
}这里虽然二维数组，但是开辟的额外空间为 常数个， 空间复杂度：O(1)
