优先队列PriorityQueue

前言
PriorityQueue这个队列不知道大家使用过吗，反正我用的很少，主要对它不是很了解，今天我带领大家剖析下PriorityQueue这个优先级队列。

PriorityQueue介绍
顾名思义，PriorityQueue是优先队列的意思。优先队列的作用是能保证每次取出的元素都是队列中权值最小的。这里牵涉到了大小关系，元素大小的评判可以通过元素本身的自然顺序（natural ordering），也可以通过构造时传入的比较器。

PriorityQueue实现了Queue接口，最大的特点是存取具有优先级，就是根据元素的顺序来决定
PriorityQueue是一个无界的容器
PriorityQueue底层是基于堆实现的不允许放入null元素
PriorityQueue不是线程安全的

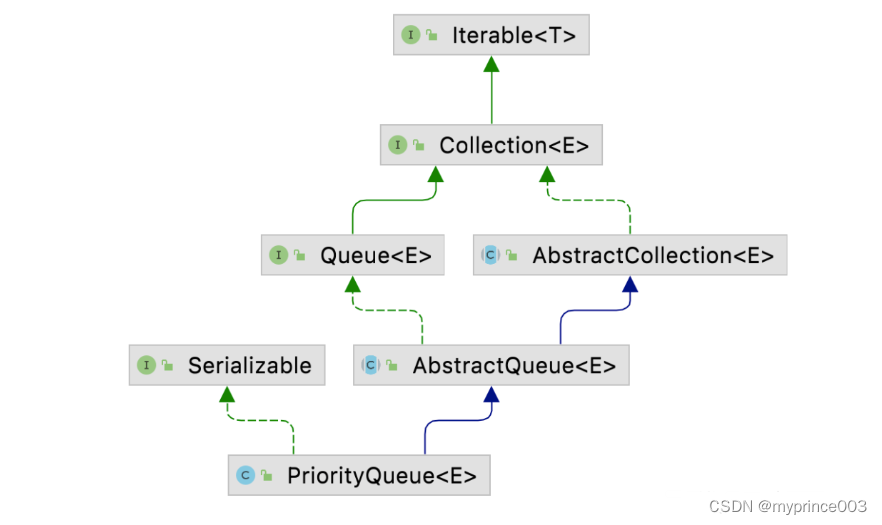
在这里插入图片描述
以上是PriorityQueue的类图,

继承了AbstractQueue抽象类，实现了Queue接口，具备队列的操作方法
实现了Seriablizable接口，支持序列化
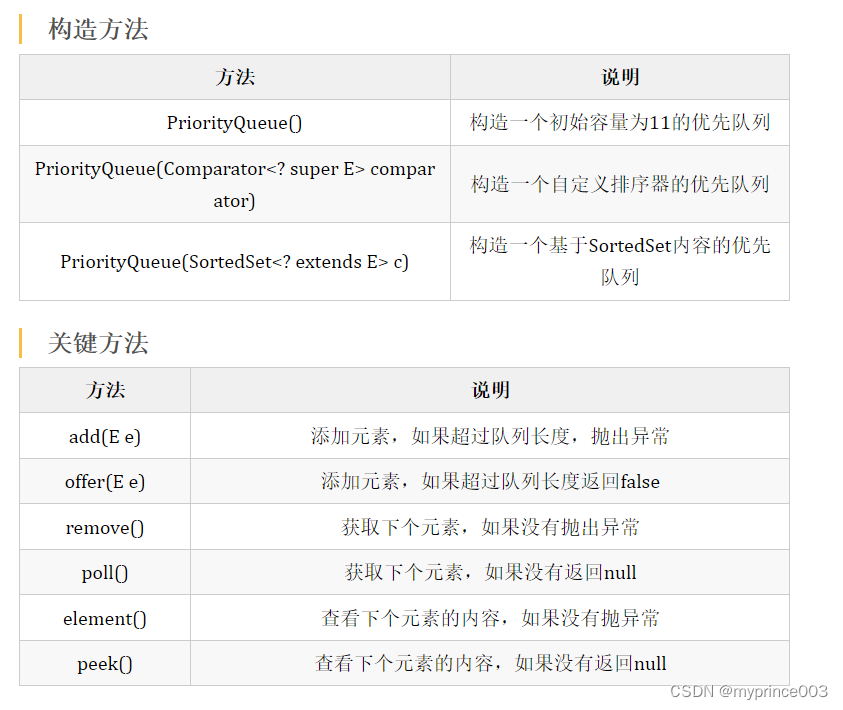
在这里插入图片描述
使用案例
优先队列功能测试

@Testpublic void test1() {Queue<Integer> queue = new PriorityQueue<>();queue.offer(5);queue.offer(4);queue.offer(1);queue.offer(9);queue.offer(3);queue.offer(2);// 打印，排序Integer poll = null;while ((poll = queue.poll()) != null) {System.out.println(poll);}}

运行结果：
在这里插入图片描述
自定义排序器

@Testpublic void test2() {// 自定义排序，倒序Queue<Integer> queue = new PriorityQueue<>(Collections.reverseOrder());queue.offer(5);queue.offer(4);queue.offer(1);queue.offer(9);queue.offer(3);queue.offer(2);// 打印，排序Integer poll = null;while ((poll = queue.poll()) != null) {System.out.println(poll);}}

运行结果：
在这里插入图片描述
实现机制
PriorityQueue通过堆实现，具体说是通过完全二叉树（complete binary tree）实现的小顶堆（任意一个非叶子节点的权值，都不大于其左右子节点的权值），也就意味着可以通过数组来作为PriorityQueue的底层实现。
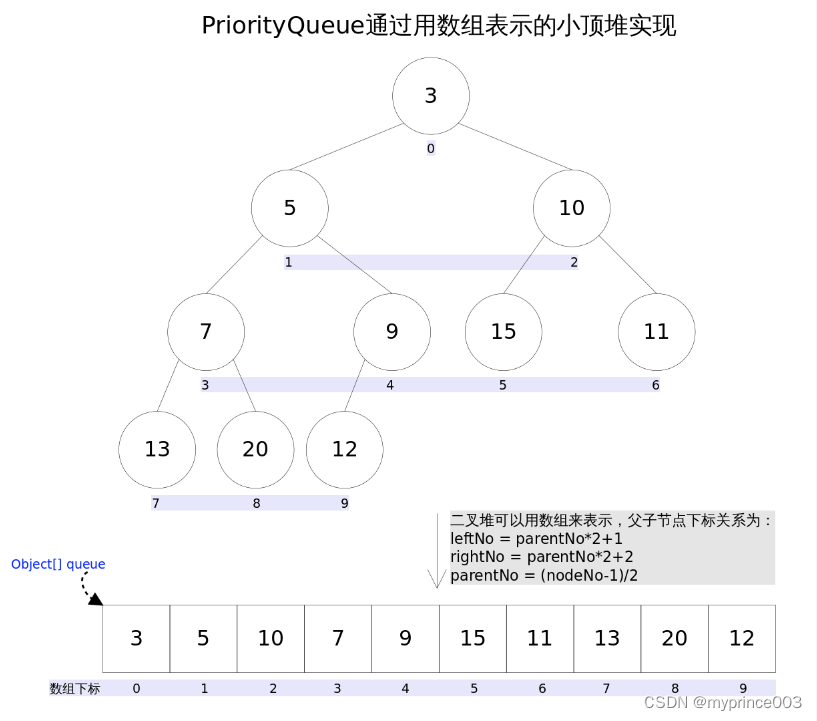
在这里插入图片描述
上图中我们给每个元素按照层序遍历的方式进行了编号，如果你足够细心，会发现父节点和子节点的编号是有联系的，更确切的说父子节点的编号之间有如下关系：

leftNo = parentNo*2+1

rightNo = parentNo*2+2

parentNo = (nodeNo-1)/2

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。

方法剖析
add()和offer()
add(E e)和offer(E e)的语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则则会返回false。对于PriorityQueue这两个方法其实没什么差别。
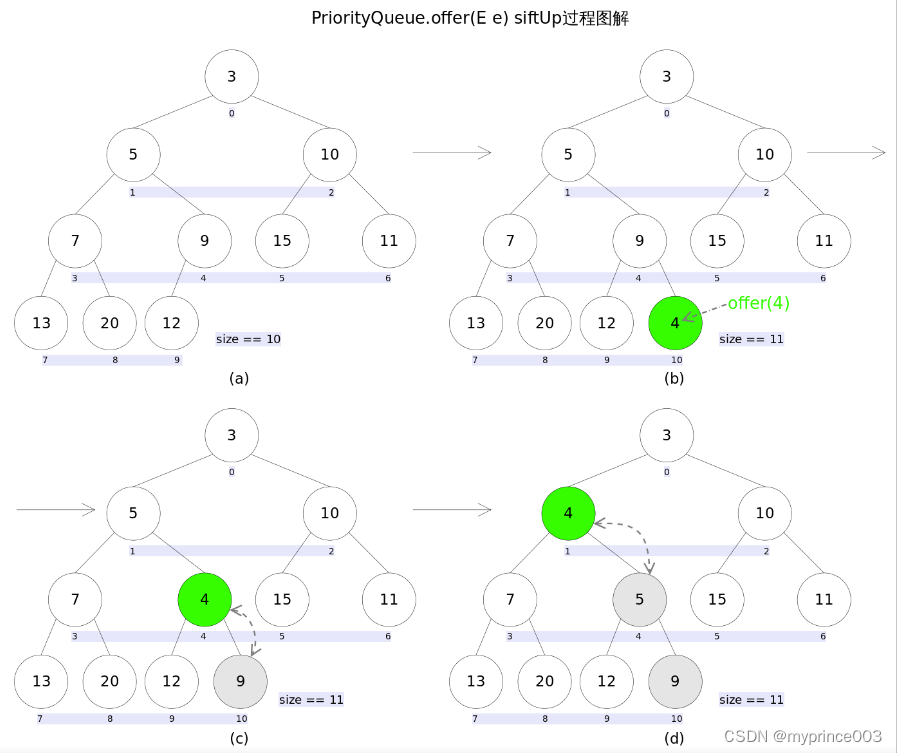
在这里插入图片描述
新加入的元素可能会破坏小顶堆的性质，因此需要进行必要的调整。

//offer(E e)
public boolean offer(E e) {if (e == null)//不允许放入null元素throw new NullPointerException();modCount++;int i = size;if (i >= queue.length)grow(i + 1);//自动扩容size = i + 1;if (i == 0)//队列原来为空，这是插入的第一个元素queue[0] = e;elsesiftUp(i, e);//调整return true;
}

上述代码中，扩容函数grow()类似于ArrayList里的grow()函数，就是再申请一个更大的数组，并将原数组的元素复制过去，这里不再赘述。需要注意的是siftUp(int k, E x)方法，该方法用于插入元素x并维持堆的特性。


//siftUp()
private void siftUp(int k, E x) {while (k > 0) {int parent = (k - 1) >>> 1;//parentNo = (nodeNo-1)/2Object e = queue[parent];if (comparator.compare(x, (E) e) >= 0)//调用比较器的比较方法break;queue[k] = e;k = parent;}queue[k] = x;
}

新加入的元素x可能会破坏小顶堆的性质，因此需要进行调整。调整的过程为：从k指定的位置开始，将x逐层与当前点的parent进行比较并交换，直到满足x >= queue[parent]为止。注意这里的比较可以是元素的自然顺序，也可以是依靠比较器的顺序。

element()和peek()
element()和peek()的语义完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素，二者唯一的区别是当方法失败时前者抛出异常，后者返回null。根据小顶堆的性质，堆顶那个元素就是全局最小的那个；由于堆用数组表示，根据下标关系，0下标处的那个元素既是堆顶元素。所以直接返回数组0下标处的那个元素即可。

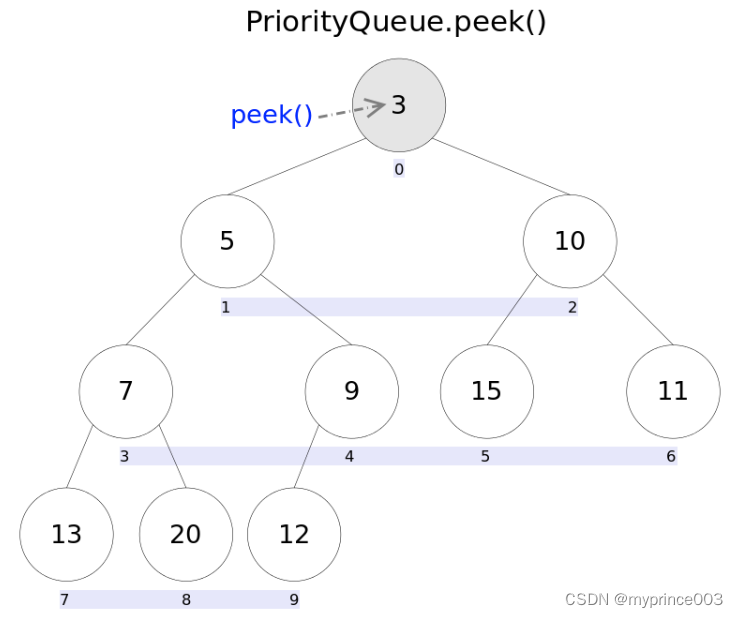
在这里插入图片描述

代码也就非常简洁：//peek()
public E peek() {if (size == 0)return null;return (E) queue[0];//0下标处的那个元素就是最小的那个
}

remove()和poll()
remove()和poll()方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。
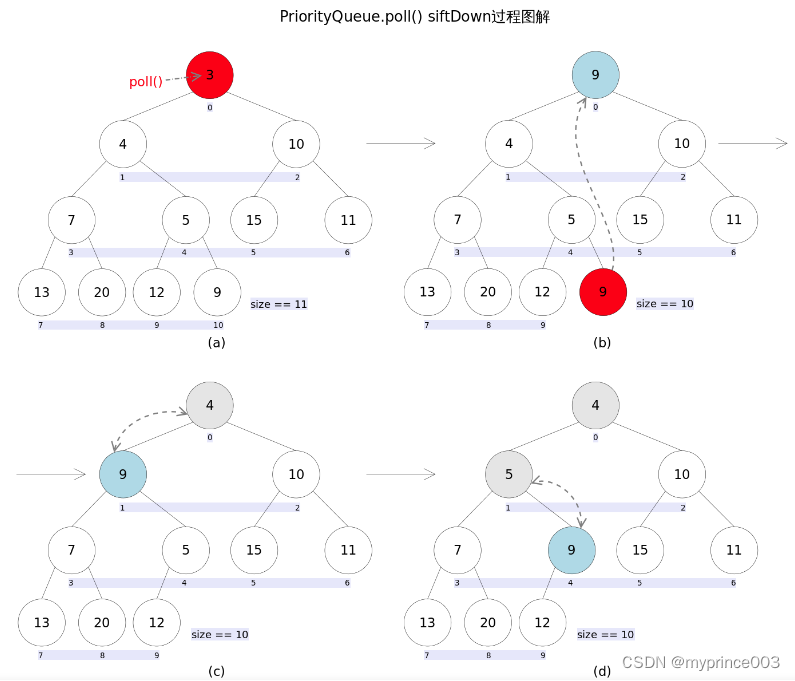
在这里插入图片描述
代码如下：

public E poll() {if (size == 0)return null;int s = --size;modCount++;E result = (E) queue[0];//0下标处的那个元素就是最小的那个E x = (E) queue[s];queue[s] = null;if (s != 0)siftDown(0, x);//调整return result;
}

上述代码首先记录0下标处的元素，并用最后一个元素替换0下标位置的元素，之后调用siftDown()方法对堆进行调整，最后返回原来0下标处的那个元素（也就是最小的那个元素）。重点是siftDown(int k, E x)方法，该方法的作用是从k指定的位置开始，将x逐层向下与当前点的左右孩子中较小的那个交换，直到x小于或等于左右孩子中的任何一个为止。

//siftDown()
private void siftDown(int k, E x) {int half = size >>> 1;while (k < half) {//首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标int child = (k << 1) + 1;//leftNo = parentNo*2+1Object c = queue[child];int right = child + 1;if (right < size &&comparator.compare((E) c, (E) queue[right]) > 0)c = queue[child = right];if (comparator.compare(x, (E) c) <= 0)break;queue[k] = c;//然后用c取代原来的值k = child;}queue[k] = x;
}

remove(Object o)
remove(Object o)方法用于删除队列中跟o相等的某一个元素（如果有多个相等，只删除一个），该方法不是Queue接口内的方法，而是Collection接口的方法。由于删除操作会改变队列结构，所以要进行调整；又由于删除元素的位置可能是任意的，所以调整过程比其它函数稍加繁琐。具体来说，remove(Object o)可以分为2种情况：1. 删除的是最后一个元素。直接删除即可，不需要调整。2. 删除的不是最后一个元素，从删除点开始以最后一个元素为参照调用一次siftDown()即可。此处不再赘述。
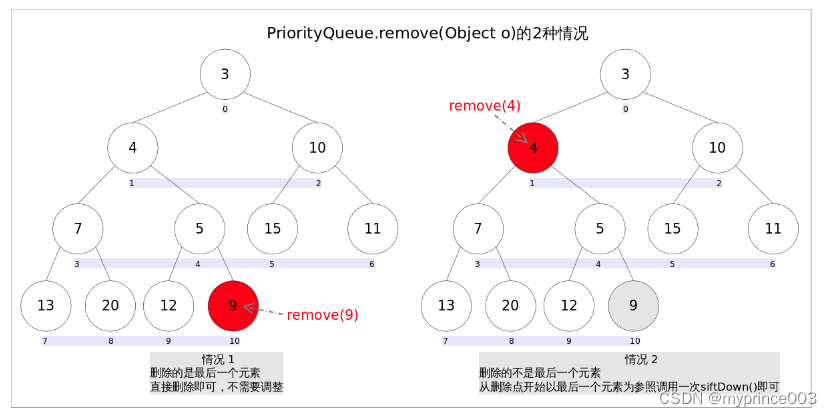
在这里插入图片描述
具体代码如下：

//remove(Object o)
public boolean remove(Object o) {//通过遍历数组的方式找到第一个满足o.equals(queue[i])元素的下标int i = indexOf(o);if (i == -1)return false;int s = --size;if (s == i) //情况1queue[i] = null;else {E moved = (E) queue[s];queue[s] = null;siftDown(i, moved);//情况2......}return true;
}