前面定义了矩阵的列空间和零空间,那么如何求得这些子空间呢?
1. 计算零空间 Nullspace
A的零空间即满足Ax=0的所有x构成的向量空间
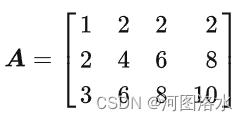
对于矩阵A进行“行操作”并不会改变Ax=b的解,因此也不会改变零空间 unchanged
第一步消元:
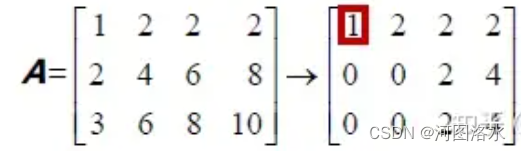

echelon 阶梯型 pivot columns and free columns
rank of A = # of pivots r=2 = # of pivot variables
n-r = 4-2 =# of free variables
2. 特解 Special solutions
当我们将系数矩阵变换为上三角阵U时,就可以用回代求得方程Ux=0的解--x1, x3可以通过回代得到 UX=0
对自由变量(free variable)x2和x4我们可以进行赋值
例如令x2=1而x4=0

可得一解
x=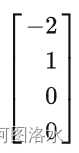
取自由变量中x2=0而x4=1
可得到另一解
x=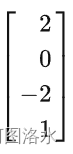
矩阵A的零空间就是这些“特解” special solution 向量的线性组合所构成的向量空间
x=c +d
+d which is a line
which is a line
n-r=特解的数目=零空间的维数
3. 行最简阶梯矩阵 Reduced row echelon form (rref)
rref(A)

notice that = I is in pivot rows/cols
在矩阵中主元行和主元列的交汇处存在一个单位阵。通过“列交换”,可以将矩阵R中的主元列集中在左侧,从而在左上角形成这个单位阵,而将自由列集中在矩阵的右侧。如果矩阵A中的某些行是线性相关的,则在矩阵R的下半部分就会出现一些完全为0的行向量
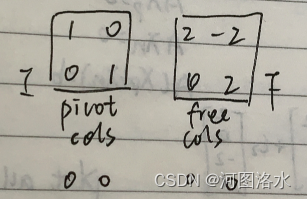
rref form
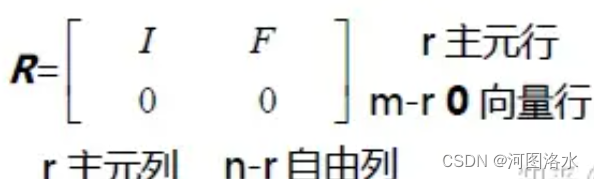
nullspace matrix ( columns = special solutions)
RN=0
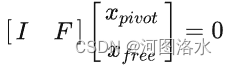
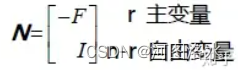
Xpivot=-FXfree
eg.













)






