题目：Pre-Training Identification of Graph Winning Tickets in Adaptive Spatial-Temporal Graph Neural Networks

作者：Wenying Duan, Tianxiang Fang, Hong Rao, Xiaoxi He

机构：南昌大学，澳门大学

arXiv网址：https://arxiv.org/abs/2406.08287

Cool Paper：https://papers.cool/arxiv/2406.08287
Code: https://anonymous.4open.science/r/paper-1430

关键词：：自适应时空图神经网络，彩票假设，图中奖票，计算效率。

TL; DR:本文提出了一种新方法，通过预训练识别图神经网络中的高效子网络（图中奖票），显著提高了自适应时空图神经网络的计算效率，同时保持了模型性能。

12 Pages 1 Preliminaries 1.5 Methodology 3.75 Experiments 1 Appendix

该研究团队在KDD23也有一篇对ASTGNNs（自适应时空图神经网络）的研究：

2023 [KDD] Localised Adaptive Spatial-Temporal Graph Neural Network

TL;DR: 对于自适应时空图神经网络（ASTGNN）在测试（推理）阶段图结构的空间信息是冗余的，训练是必要的。

🌟【紧跟前沿】“时空探索之旅”与你一起探索时空奥秘！🚀
欢迎大家关注时空探索之旅

摘要

在本文中，提出了一种新方法，通过引入源自彩票假设 (Lottery Ticket Hypothesis，LTH) 的图中奖彩票 (Graph Winning Ticket，GWT) 概念，显著提高自适应时空图神经网络 (ASTGNN) 的计算效率。通过在训练之前采用预先确定的星型拓扑作为 GWT，本文在边缘减少和高效信息传播之间取得平衡，在保持高模型性能的同时降低了计算需求。生成自适应时空图的时间和空间计算复杂度都从$$O(N^2)$$ 显著降低到 $$O(N)$$。本文的方法简化了 ASTGNN 部署，消除了对详尽训练、剪枝和再训练周期的需求，并在各种数据集上通过实证证明，有可能以低得多的计算成本实现与完整模型相当的性能。具体来说，本文的方法能够使用配备 48 GB 显存的单张 A6000 在最大规模时空数据集上训练 ASTGNN，克服了原始训练中遇到的内存不足问题，甚至达到了最先进的性能。此外，本文从谱图理论的角度深入研究了 GWT 的有效性，提供了大量的理论支持。这一进步不仅证明了 ASTGNN 中存在高效子网络，而且拓宽了 LTH 在资源受限环境中的适用性，标志着图神经网络领域的重大进步。

Q: 这篇论文试图解决什么问题？

A: 这篇论文提出了一种新的方法，旨在显著提高自适应时空图神经网络（Adaptive Spatial-Temporal Graph Neural Networks，简称ASTGNNs）的计算效率。具体来说，论文通过引入基于彩票假设（Lottery Ticket Hypothesis，简称LTH）的图中奖票（Graph Winning Ticket，简称GWT）的概念，以期在减少计算需求的同时保持模型性能。

ASTGNNs在处理大规模时空数据时面临显著的计算开销挑战，这主要是因为它们需要学习完整的图上的自适应邻接矩阵，并且聚合阶段计算密集。论文的主要贡献包括：

1. 提出了一种在训练前确定GWT的方法，通过采用预定的星型拓扑作为GWT，平衡了边的减少和有效信息传播之间的关系，从而在降低计算需求的同时保持了高性能。
2. 通过实验验证了这种方法在多个数据集上与完整模型相比具有可比性，甚至在某些情况下性能更优，同时显著降低了训练和推理的计算成本。
3. 从谱图理论的角度深入探讨了GWT的有效性，为LTH在资源受限环境中的适用性提供了理论支持。

这种方法不仅证明了ASTGNNs内存在高效的子网络，而且扩展了LTH在资源受限设置中的适用性，是图神经网络领域的重要进展。

Q: 有哪些相关研究？

A: 论文中提到了多个与时空图神经网络（STGNNs）和彩票假设（LTH）相关的研究领域和具体工作。以下是一些主要的相关研究：

1. 时空图神经网络（STGNNs）: 这类网络专注于分析时空数据，特别是动态信号在不同空间域之间的相互作用。STGNNs能够建模节点之间的空间依赖性，并且通过学习邻接矩阵来有效捕捉数据的潜在模式。
2. 预定义和自学习方法: STGNNs可以根据构建邻接矩阵的方法分为预定义方法和自学习方法。预定义方法使用领域知识来构建图，例如ASTGNN和STGCN利用道路网络结构。自学习方法则通过时间变化的输入动态构建图，如PDFormer和DG。
3. 彩票假设（LTH）: LTH提出了在大型神经网络中存在较小的子网络（称为“中奖彩票”），这些子网络可以在隔离训练时达到与原始网络相似的性能。这个概念已经被扩展到ASTGNNs的领域，即在可学习的时空图中识别这样的子网络，即GWTs。
4. 图彩票假设（Graph Lottery Ticket Hypothesis）: 这是LTH在图神经网络（GNNs）中的扩展，研究者通过迭代应用UGS来识别图彩票。
5. ASTGNN模型: 如Graph WaveNet和AGCRN，这些模型通过随机初始化的可学习节点嵌入来促进自适应图的生成。
6. 谱图理论: 论文还深入探讨了谱图理论，为GWT的有效性提供了理论支持。
7. 其他STGNNs: 论文中还提到了其他几种STGNNs，包括DGCRN、MegaCRN、STGODE、D2STGNN和DSTAGNN，这些模型代表了该领域的最新趋势。
8. 图结构的稀疏化: 论文中提到了AGS方法，这是一种通过稀疏化空间图来提高ASTGNNs推理效率的先前工作。

这些相关研究为理解论文提出的GWT方法提供了背景，并展示了该方法在现有研究基础上的创新和改进。

Q: 论文如何解决这个问题？

A: 论文通过以下几个关键步骤解决了提高ASTGNNs计算效率的问题：

1. 引入图中奖票（GWT）概念：基于彩票假设（LTH），论文提出了图中奖票的概念，这是一种存在于ASTGNNs可学习空间图中的高效子网络，可以在减少计算成本的同时保持模型性能。
2. 预确定星型拓扑：论文提出使用星型拓扑作为GWT，这种拓扑结构在减少边数的同时，仍然保持了有效的信息传播能力。星型拓扑的直径为2，可以在两层AGCN中实现全局空间依赖性的建模。
3. 降低计算复杂度：通过使用星型拓扑，论文将生成自适应时空图的时间和内存计算复杂度从O(𝑁^2)显著降低到O(𝑁)。
4. 简化训练过程：论文的方法避免了传统训练过程中的迭代训练、剪枝和重训练的需要，从而简化了ASTGNNs的部署。
5. 理论和实证分析：论文从谱图理论的角度提供了对GWT有效性的深入分析，并在多个数据集上通过实验验证了星型拓扑作为GWT的性能。
6. 提出GWT-AGCN层：为了进一步提高效率和硬件兼容性，论文提出了一种新的GWT-AGCN层，该层使用矩阵乘法和标准激活函数，与传统AGCN层相比，具有更低的计算复杂度和更好的硬件兼容性。
7. 中心节点选择和初始化：论文讨论了中心节点选择的重要性，并提出了一种平均初始化方法，以确保中心节点嵌入向量位于节点嵌入空间的物理中心，从而提高模型的预测精度。

通过这些方法，论文不仅提高了ASTGNNs的计算效率，还保持了模型性能，甚至在某些情况下达到了最先进的性能水平。

Q: 论文做了哪些实验？

A: 论文中进行了一系列实验来验证所提出方法的有效性，实验主要包括以下几个方面：

1. 实验设置：
   • 使用了两种典型的ASTGNN架构：AGCRN和Graph WaveNet (GWNET)。
   • 在五个大型时空数据集上进行实验，包括PEMS07、SD、GBA、GLA和CA。
2. 性能评估：
   • 使用了三个标准的预测准确度指标：平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）。
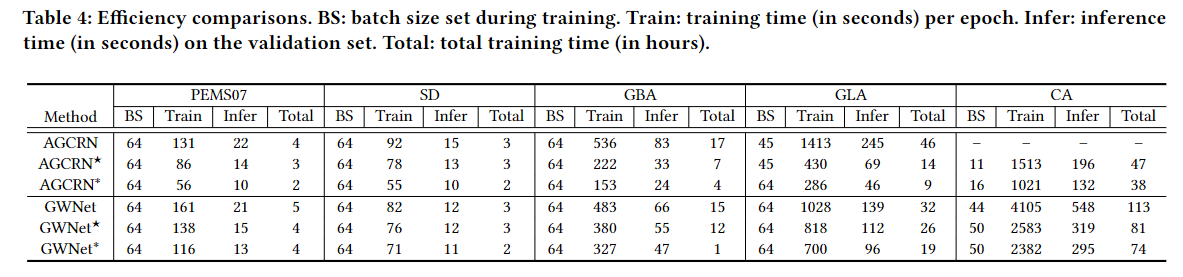
3. 效率评估：
   • 评估了模型训练和推理的墙钟时间。
   • 报告了训练过程中的批量大小，以反映模型处理大规模数据集的能力。
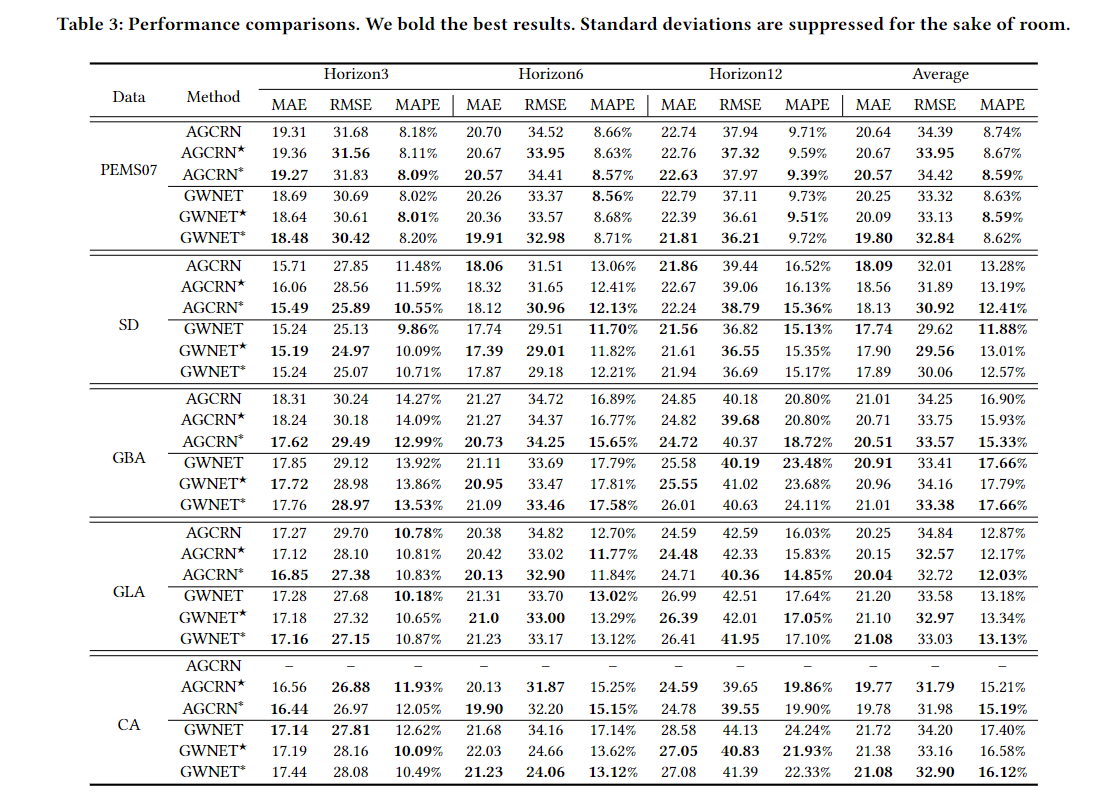
4. 主要结果：
   • 展示了AGCRN和GWNET在不同数据集上的性能和效率比较。
   • 证明了在所有数据集上，使用GWT的ASTGNNs（AGCRN★和GWNET★）与原始模型相比具有可比或更优的性能。
5. 收敛性分析：
   • 展示了原始AGCRN和AGCRN★在PEMS07和SD数据集上的损失和测试MAE曲线，证明了预确定的GWT确保了与完整图模型同样一致、快速和稳定的收敛性。
6. 与最新技术比较：
   • 将AGCRN和GWNET与当前最先进的STGNNs进行了比较，包括DGCRN、MegaCRN、STGODE、D2STGNN和DSTAGNN。
7. 节点嵌入初始化的影响分析：
   • 对AGCRN★进行了消融研究，比较了平均初始化和随机初始化对模型预测精度的影响。
8. 与AGS方法的比较：
   • 将所提出的方法与现有的AGS方法进行了比较，证明了所提出方法的优越性。
9. T★的鲁棒性分析：
   • 通过引入T★的扰动过程，研究了T★的连通性对ASTGNN建模全局空间依赖性的重要性。

这些实验全面评估了所提出方法在不同方面的表现，包括预测准确性、计算效率、收敛速度、鲁棒性等，从而为论文的主张提供了有力的实证支持。

Q: 总结一下论文的主要内容

A: 这篇论文的主要内容可以概括为以下几个要点：

1. 问题提出：论文针对自适应时空图神经网络（ASTGNNs）在大规模时空数据上的训练和推理阶段存在的高计算开销问题，提出了一种新的方法来提高计算效率。
2. 方法介绍：引入了基于彩票假设（LTH）的图中奖票（GWT）概念，通过预训练前确定星型拓扑结构作为GWT，以减少边数同时保持有效信息传播，从而降低计算复杂度。
3. 理论支持：利用谱图理论为星型拓扑的有效性提供了理论分析和证明，证明了星型拓扑是完整图的一个良好近似，能够学习到空间时间依赖性。
4. 实验验证：在多个大型时空数据集上进行了实验，验证了使用GWT的ASTGNNs在保持或甚至超越完整模型性能的同时，显著降低了计算成本。
5. 效率和性能：论文的方法不仅减少了模型的计算需求，还展示了在不同数据集上与现有模型相比的可比性或优越性。
6. 简化训练过程：通过预确定GWT，避免了传统训练过程中的迭代训练、剪枝和重训练的需要，简化了ASTGNNs的部署。
7. GWT-AGCN层：提出了GWT-AGCN层，提高了模型的硬件兼容性和计算效率。
8. 中心节点选择：讨论了中心节点选择的重要性，并提出了平均初始化方法来提高模型的预测精度。
9. 未来工作：论文最后提出了一些可能的研究方向，包括长期预测、不同拓扑结构的GWT、跨领域适用性等。

出了GWT-AGCN层，提高了模型的硬件兼容性和计算效率。
8. 中心节点选择：讨论了中心节点选择的重要性，并提出了平均初始化方法来提高模型的预测精度。
9. 未来工作：论文最后提出了一些可能的研究方向，包括长期预测、不同拓扑结构的GWT、跨领域适用性等。

总的来说，这篇论文在理论和实践层面都为ASTGNNs的效率和实用性提供了显著的改进，并通过实验验证了其有效性。