基础拓扑

有限集、可数集和不可数集

2.1 定义 考虑两个集$A$和$B$，他们的元素可以是任何东西。假定对于$A$的每个元素$x$，按照某种方式，与集$B$的一个元素联系着，这个元素记作$f\left(x\right)$;那么，就说$f$是从$A$到$B$的一个函数（或将$A$映入$B$内的一个映射）。集$A$叫做$f$的定义域（domain, 或者说$f$定义在$A$上），而元素$f\left(x\right)$叫做$f$的值(value)。$f$的一切值得集叫做$f$得值域(range)

2.2 定义 设$A$和$B$是两个集，$f$是$A$到$B$内的一个映射。如果$E\subset A$， f ( E ) = { f ( x ) : x ∈ E } f\left( E \right)=\left\{ f\left( x \right): x \in E\right\} f(E)={f(x):x∈E}。我们称$f\left(E\right)$为$E$在$f$之下的象(image)。按这个记法来说，$f\left(A\right)$就是$f$的值域。显然$f\left(A\right)\subset B$.如果$f\left(A\right)=B$，就说$f$将$A$映满$B$（也是离散里的满射）
‌‌‌‌　　$E\subset B$时， f − 1 ( E ) = { x ∈ A : f ( x ) ∈ E } f^{-1} \left( E \right)=\left\{ x\in A: f\left( x \right)\in E \right\} f−1(E)={x∈A:f(x)∈E}。称$f^{-1}\left(E\right)$为$f$之下的逆象(inverse image)。$y\in B$时， f − 1 ( y ) = { x ∈ A : f ( x ) = y } f^{-1}\left( y \right)=\left\{x\in A: f\left( x \right)=y \right\} f−1(y)={x∈A:f(x)=y}。如果$f^{-1}\left(y\right)$对于每个$y\in B$至多含有$A$中的一个元素，那么就称$f$是$A$到$B$内的1-1（一对一的）映射。这句话也可以这么表述如下：如果对于$x_1\in A,x_2\in B$，当$x_1\ne x_2$时，$f\left(x_1\right)\ne f\left(x_2\right)$，那么$f$就是$A$到$B$内的一个1-1映射（也是离散里面的单射）

(后面双射=单射+满射)

2.3 定义 如果存在$A$到$B$上的双射，那么就说$A$和$B$可以建立1-1对应，或者说$A$和$B$具有相同的基数，或者就简单地说$A$和$B$等价，并且记作$A\sim B$这个关系显然具有下列性质
‌‌‌‌　　自反性：$A\sim A$
‌‌‌‌　　对称性：如果$A\sim B$,就有$B\sim A$
‌‌‌‌　　传递性：如果$A\sim B$并且$B\sim C$，就有$A\sim C$
‌‌‌‌　　任何具有这三个性质的关系都叫做等价关系

2.4 定义 对于任意正整数$n$，令 J n = { 1 , 2 , ⋯ , n } J_{n}=\left\{ 1,2,\cdots, n \right\} Jn​={1,2,⋯,n}，令$J={\mathbb{N}}_{+}$,设$A$是任意一个集，我们说
(a)$A$是有限的，如果对于某个$n$，$A\sim J_n$(空集也认为是有限集)
(b)$A$是无限的，如果$A$不是有限的
©$A$是可数的(countable)，如果$A\sim J$
(d)$A$是不可数的(uncountable)，如果$A$既不是有限的，也不是可数的
(e)$A$是至多可数的(at most countable)，如果$A$或为有限或为可数的
可数集有时候也叫做可枚举集(enumerable)或可列集(denumerable)

2.7 定义 定义在$J$上的函数叫做一个序列，如果对于一切$n\in J,f\left(n\right)=x_n$,习惯上就把序列$f$用符号 { x n } \left\{ x_{n} \right\} {xn​}来表示，或者用$x_1,x_2,\cdots$来表示。$f$的值，即元素$x_n$，叫做这个序列的项。设$A$是一个集并且对一切$n\in J,x_n\in A$，那么 { x n } \left\{ x_{n} \right\} {xn​}就叫做$A$里的一个序列，或者叫做$A$的元素的一个序列。
‌‌‌‌　　注意，一个序列的项不一定各不相同

2.8 定理 可数集$A$的每个无限子集也是可数集
证明：
‌‌‌‌　　设$E\subset A$，并且$E$是无限集。把$A$的元素$x$排成一个不同元素的序列 { x n } \left\{ x_{n} \right\} {xn​}。按以下方式作序列 { n k } \left\{ n_{k} \right\} {nk​}
‌‌‌‌　　令$n_1$是使$x_{n_1}\in E$的最小正整数。当$n_1,\cdots ,n_{k-1}$选定以后，$n_k$是大于$n_{k-1}$并且使$x_{n_k}\in E$的最小正整数
‌‌‌‌　　令$f\left(k\right)=x_{n_k}$，我们得到了$E$和$J$之间的一个双射

2.9 定义 设$A$和$\Omega$都是集。假定对于$A$的每个元素$\alpha$,与$\Omega$的一个子集联系着，这个子集记作$E_{\alpha }$
用 { E α } \left\{ E_{\alpha} \right\} {Eα​}来表示以集$E_{\alpha }$为元素的集。我们有时不说集的集，而说一组集或一簇集。
许多集$E_{\alpha }$的并是指这样一个集合$S$：$x\in S$当且仅当至少对于一个$\alpha \in A$，有$x\in E_{\alpha }$，表示并的记号是
$$S=\bigcup _{\alpha \in A}{E}_{\alpha }$$
如果由整数$1,2,\cdots ,n$组成，又往往写作：
$$S=\bigcup _{m=1}^n{E}_m$$
或
$$S=E_1\cup E_2\cup \cdots \cup E_n$$
如果$A$是一切正整数的集，通常的记号是
$$S=\bigcup _{m=1}^{\infty }{E}_m$$
注意这里的$\infty$仅仅表示对于集的可数组来取并

如果$A\cap B$不空，就说$A$与$B$相交，否则就说他们不相交

2.12 定理 设 { E n } \left\{ E_{n} \right\} {En​}是可数集组成的序列，令
$$S=\bigcup _{n=1}^{\infty }{E}_n$$
那么$S$是可数的
证明：把每个集$E_n$排成一个序列 { x n k } \left\{ x_{nk} \right\} {xnk​}，而来考虑无限阵列

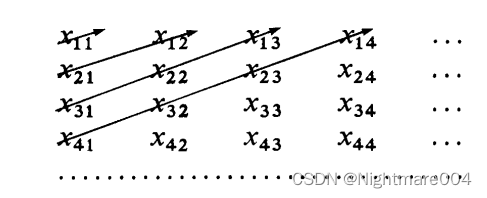
在这个阵列里，$E_n$的元素构成第$n$行。这个阵列含有$S$的一切元素，这些元素可以按照箭头所指出的顺序排列称成一个序列
$$x_{11};x_{21},x_{12};x_{31},x_{22},x_{13};x_{41},x_{32},x_{23},x_{14};\cdots$$
这些集$E_n$的任何两个两个，如果有公共元素，那么这些元素将在这个序列中出现不止一次。因此一切正整数的集里有一个子集$T$，使得$S\sim T$这就证明了$S$是至多可数的。因为$E_1\subset S$，而$E_1$是无限多的，所以$S$也是无限的，从而使可数的
推论 假定$A$是至多可数的，并且对应于每个$\alpha \in A$的$B_{\alpha }$是至多可数的。令
$$T=\bigcup _{\alpha \in A}{B}_{\alpha }$$
那么$T$是至多可数的

2.13 定理 设$A$是可数集。又假设$B_n$是一切$n$元素组$\left(a_1,a_2,\cdots ,a_n\right)$的集，这里$a_k\in A$,并且元素$a_1,a_2,\cdots ,a_n$不一定相同，那么$B_n$是至多可数的
证明：
$B_1$显然是可数的，因为$B_1=A$。假设$B_{n-1}$是可数的，那么，$B_n$的元素具有形式
$$\left(b,a\right)\left(b\in B_{n-1},a\in A\right)$$
对于每个固定的$b$，元素对$\left(b,a\right)$的集与$A$等价，因而是可数的。
于是 B n = ⋃ b ∈ B n − 1 { ( b , a 1 ) , ⋯ , ( b , a n ) , ⋯ } B_n= \bigcup_{b\in B_{n-1}}\left\{ \left( b,a_{1} \right),\cdots,\left( b,a_{n} \right),\cdots \right\} Bn​=⋃b∈Bn−1​​{(b,a1​),⋯,(b,an​),⋯}是可数集
于是由归纳法证明了这个定理
推论 一切有理数的集是可数的
证明：
每个有理数$r=\frac{b}{a}$,这里$a,b\in Z$,一切数对$\left(b,a\right)$的集是可数的。从而一切分数$\frac{b}{a}$的集是可数的
实际上一切代数数的集也是可数的

2.14 定理 设$A$是由数码$0$和$1$构成的一切序列的集，这个集$A$是不可数的
$A$的元素都是像$1,0,0,1,0,1,1,1,\cdots$这样的序列
证明：设$E$是$A$的一个可数子集，并且设$E$由一列元素$s_1,s_2,s_3,\cdots$组成
现在构造一个序列如下，如果在$s_n$里，第$n$个数码是$1$，就令$s$的第$n$个数码取0，否则就取$1$。于是序列$s$与$E$里的每个序列至少有一位不同，从而$s\notin E$。然而显然$s\in A$，所以$E$是$A$的真子集
这就证明了$A$的每个可数子集是$A$的真子集，因此$A$是不可数集（否则$A$将是它自己的一个真子集，这是不可能的）

以上证法的思想是Cantor首先使用的，并且称为Cantor的对角线手法

度量空间

2.15 定义：设$X$是一个集。他的元素叫做点，如果$X$的任意两点$p$和$q$，联系于一个实数$d\left(p,q\right)$，叫做从$p$到$q$的距离，它合乎条件：
(a) 如果$p\ne q$,那么$d\left(p,q\right)>0;d\left(p,p\right)=0$
(b) $d\left(p,q\right)=d\left(q,p\right)$
© 对于任意$r\in X,d\left(p,q\right)\le d\left(p,r\right)+d\left(r,q\right)$
就称$X$是一个度量空间
具有这三条性质的函数叫做距离函数或度量

2.18 定义：设$X$是一个度量空间，下面提到的一切点和一切集，都理解为$X$的点和集
(a) 点$p$的邻域$N_r\left(p\right)$指的是满足条件$d\left(p,q\right)<r$的一切点$q$所成的集，数$r$叫做$N_r\left(p\right)$的半径
(b) 点$p$叫做集$E$的极限点，如果$p$的邻域都含有一点$q\in E$而$q\ne p$
© 如果$p\in E$并且$p$不是$E$的极限点，那么$p$就叫做$E$的孤立点
(d) $E$叫做闭的，如果$E$的每个极限点都是$E$的点
(e) 点$p$叫做$E$的一个内点，如果存在$p$的一个邻域$N$,有$N\subset E$
(f) $E$叫做开的，如果$E$的每个点都是$E$的内点
(g) $E$的余集（记作$E^c$）指的是一切合于$p\in X$及$p\notin E$的点$p$的集
(h) $E$叫做完全的（perfect），如果$E$是闭集，并且$E$的每个点都是$E$的极限点
(i) $E$叫做有界的，如果有一个实数$M$和一个点$q\in X$，使得一切$p\in E$都满足$d\left(p,q\right)<M$
(j) $E$叫做在$X$中稠密的，如果$X$额每个点都是$E$的极限点，或是$E$的点（或兼此二者）

2.19 定理：邻域必是开集
证明：
设$E=N_r\left(p\right)$, 令$q$是$E$的任意一点。于是又一正实数$h$，使得
$$d\left(p,q\right)=r-h$$
对于一切合适条件$d\left(q,s\right)<h$的点$s$，我们有
$$d\left(p,s\right)\le d\left(p,q\right)+d\left(q,s\right)<r-h+h=r$$
所以$s\in E$,因此，$q$是$E$的内点

2.20 定理：如果$p$是集$E$的一个极限点，那么$p$的每个邻域含有$E$的无限多个点
证明：
假设有$p$的某个邻域$N$只含有$E$的有限个点，令$q_1,\cdots ,q_n$是$N\cap E$中哲有限个异于$p$的点
又令
$$r=\underset{1\le m\le n}{\min }d\left(p,q_m\right)$$
显然$r>0$
邻域$N_r\left(p\right)$不能再含有$E$的点$q$而$q\ne p$的了，所以$p$不是$E$的极限点，矛盾
推论：有限的点集没有极限点

2.22 定理：设 { E α } \left\{ E_{\alpha} \right\} {Eα​}是若干（有限个或无限多个）集$E_{\alpha }$的一个组，那么
$${\left(\bigcup _{\alpha }{E}_{\alpha }\right)}^c=\bigcap _{\alpha }\left(E_{\alpha }^c\right)$$
证明：
令$A={\left({\bigcup }_{\alpha }{E}_{\alpha }\right)}^c,B={\bigcap }_{\alpha }\left(E_{\alpha }^c\right)$
如果$x\in A$，那么$x\notin {\bigcup }_{\alpha }{E}_{\alpha }$ ，因此$\forall \alpha ,x\notin E_{\alpha }$，从而$\forall \alpha ,x\in E_{\alpha }^c$,因此$x\in B$, 即$A\subset B$
如果$x\in B$，那么$\forall \alpha ,x\in E_{\alpha }^c$，因此$\forall a,x\notin E_{\alpha }$，从而$\forall \alpha ,x\notin {\bigcup }_{\alpha }{E}_{\alpha }$,于是$x\in A$，即$B\subset A$
这就证明了$A=B$

2.23 定理：$E$是开集当且仅当它的余集是闭集
证明：首先设$E^c$是闭集，取$x\in E$，那么$x\notin E^c$，于是存在$x$的邻域$N$，使得$E^c\cap N$为空集，这就是说$N\subset E$， 所以$x$是$E$的内点

其次，设$E$是开集，令$x$是$E^c$的极限点，那么$x$的每个邻域含有$E^c$的点，，所以$x$不是$E$的内点，因为$E$是开集，这就是说$x\in E^c$,因此$E^c$是闭集
推论：$F$是闭集当且仅当它的余集是开集

2.24 定理：
(a) 任意一组开集 { G α } \left\{ G_{\alpha} \right\} {Gα​}的并${\bigcup }_{\alpha }{G}_{\alpha }$是开集
(b) 任意一组闭集 { F α } \left\{ F_{\alpha} \right\} {Fα​}的交${\bigcap }_{\alpha }{F}_{\alpha }$是闭集
© 任意一组有限个开集$G_1,\cdots ,G_n$的交${\bigcap }_{i=1}^n{G}_i$是开集
(d) 任意一组有限个闭集$F_1,\cdots ,F_n$的并${\bigcup }_{i=1}^n{F}_i$是闭集

证明：
令$G={\bigcup }_{\alpha }{G}_{\alpha }$。如果$x\in G$，就有某个$\alpha$，使得$x\in G_{\alpha }$.因为$x$是$G_{\alpha }$的一个内点，所以$x$也是$G$的一个内点，从而$G$是开集

由
$${\left(\bigcap _{\alpha }{F}_{\alpha }\right)}^c=\bigcup _{\alpha }\left(F_{\alpha }^c\right)$$
(b)成立

其次，令$H={\bigcap }_{i=1}^n{G}_i$,对于$x\in H$, 存在$x\in H$,存在$x$的邻域$N_i$,其半径为$r_i$,使得$N_i\subset G_i\left(i=1,2,\cdots ,n\right)$
令
$$r=\min \left(r_1,r_2,\cdots ,r_n\right)$$
又令$N$是$x$的以$r$为半径的邻域。于是对于$i=1,2,\cdots ,n,N\subset G_i$,从而$N\subset H$,所以$H$是开集
由
$${\left(\bigcap _{i=1}^n{F}_i\right)}^c=\bigcup _{i=1}^n\left(F_i^c\right)$$
(d)成立

2.25 例子：©,(d)中的有限个是必不可少的。
令$G_n=\left(-\frac{1}{n},\frac{1}{n}\right)$， 那么$G_n$是$R^1$的开子集
令 G = ⋂ n = 1 ∞ G n = { 0 } G = \bigcap_{n=1}^{\infty}G_{n}= \left\{ 0 \right\} G=⋂n=1∞​Gn​={0},不是$R^1$的开子集
因此无限个开集的交不一定是开集
同理，无限个闭集的并不一定是闭集

2.26 定义：设$X$是度量空间，如果$E\subset X$,$E^{\prime }$表示$E$在$X$中所有极限点组成的集。那么$\bar{E}=E\cup E^{\prime }$叫做$E$的闭包

2.27 定理：设$X$是度量空间，而$E\subset X$，那么
(a) $\bar{E}$闭
(b) $E=\bar{E}$当且仅当$E$闭
© 如果闭集$F\subset X$且$E\subset F$,那么$\bar{E}\subset F$
由(a)和©，$\bar{E}$是$X$中包含$E$的最小闭子集

证明：
(a)如果$p\in X$而$p\notin \bar{E}$,那么$p$既不是$E$的点，又不是$E$的极限点，因此$p$有某个邻域与$E$不交，所以${\bar{E}}^c$是开集，进而$\bar{E}$闭
(b)如果$E=\bar{E}$，则$E$闭。如果$E$闭，则$E^{\prime }\subset E$,由此$E=\bar{E}$
©如果$F$闭且$F\supset E$，那么$F\supset F^{\prime }$,因此$F\supset E^{\prime }$。于是$F\supset \bar{E}$
(这是因为$E$的极限点同样是$F$的极限点)

2.28 定理：设$E$是一个不空实数集，上有界，令$y=\sup E$，那么$y\in \bar{E}$.因此如果$E$闭，那么$y\in E$
证明：
如果$y\in E$,则$y\in \bar{E}$
如果$y\notin E$，$\forall h>0,\exists x\in E,y-h<x<y$
（$\forall x\in E,x\le y$, 如果$x=y$，则$y\in E$，如果$y-h\ge x$，则$y-h$也是$E$的上界，与$y$是最小上界矛盾）
所以$y$是$E$的极限点，因此$y\in \bar{E}$

2.29 定义：如果能给每个$p\in E$配备一个$r>0$，凡当$d\left(p,q\right)<r$且$q\in Y$时，就有$q\in E$，我们就说$E$关于$Y$是开的。
例如$\left(a,b\right)$关于$R^1$是开的，但是关于$R^2$就不是

2.30 定理：设$Y\subset X$，$Y$的子集$E$关于$Y$是开的，当且仅当$X$有某个开子集$G$，使得$E=Y\cap G$
证明：
设$E$关于$Y$是开的，那么对于每个$p\in E$，有正数$r_p$的使得当$d\left(p,q\right)<r_p$与$q\in Y$时，有$q\in E$
令 V p = { q ∈ X : d ( p , q ) < r p } = N r p ( p ) V_{p} =\left\{ q \in X:d \left( p,q \right) < r_{p} \right\}=N_{r_{p}}\left( p \right) Vp​={q∈X:d(p,q)<rp​}=Nrp​​(p)，并定义
$$G=\bigcup _{p\in E}{V}_p$$
$G$是$X$的开子集
因为一切$p\in E$都有$p\in V_p$，显然$E\subset G\cap Y$
按照$V_p$的选取，对于每个$p\in E$，我们有$V_p\cap Y\subset E$,从而$G\cap Y\subset E$。因此$E=Y\cap G$
反过来，如果$G$是$X$的一个开集，而$E=G\cap Y$，那么每个$p\in E$有一个邻域$V_p\subset G$
于是$V_p\cap Y\subset E$,所以$E$关于$Y$是开集

紧集

2.31 定义：设$E$是度量空间$X$的一个集，$E$的开覆盖(open cover)指的是$X$的一组开子集 { G α } \left\{ G_{\alpha} \right\} {Gα​}，使得$E\subset {\bigcup }_{\alpha }{G}_{\alpha }$

2.32 定义：度量空间$X$的子集$K$叫做紧的(compact)，如果$K$的每个开覆盖总含有一个有限子覆盖
说的更准确一些，这个要求就是，如果 { G α } \left\{ G_{\alpha} \right\} {Gα​}是$K$的一个开覆盖，那么总有有限多个指标${\alpha }_1,\cdots ,{\alpha }_n$使得
$$K\subset G_{{\alpha }_1}\cup \cdots \cup G_{{\alpha }_n}$$

2.33 定理：设$K\subset Y\subset X$，那么$K$关于$X$是紧的当且仅当$K$关于$Y$是紧的
证明：
设$K$关于$X$是紧的，并且设 { V α } \left\{ V_{\alpha} \right\} {Vα​}是一组关于$Y$的开的集，使得$K\subset {\bigcup }_{\alpha }{V}_{\alpha }$
由于$V_{\alpha }$是$Y$的开子集，因此$X$有某个开子集$G_{\alpha }$，使得$V_{\alpha }=Y\cap G_{\alpha }$
$K\subset {\bigcup }_{\alpha }{V}_{\alpha }={\bigcup }_{\alpha }\left(Y\cap G_{\alpha }\right)\subset {\bigcup }_{\alpha }{G}_{\alpha }$，因此 { G α } \left\{ G_{\alpha} \right\} {Gα​}是$E$的开覆盖
又因为$K$关于$X$是紧的，我们可以选出有限多个指标${\alpha }_1,\cdots ,{\alpha }_n$,使得
$$K\subset G_{{\alpha }_1}\cup \cdots \cup G_{{\alpha }_n}$$
又因为$K\subset Y$,那么
$$K\subset (G_{{\alpha }_1}\cup \cdots \cup G_{{\alpha }_n})\cap Y=V_{{\alpha }_1}\cup \cdots \cup V_{{\alpha }_n}$$

反过来，设$K$关于$Y$是紧的。令 { G α } \left\{ G_{\alpha} \right\} {Gα​}是$X$的一组开子集，并且能覆盖$K$
令$V_{\alpha }=Y\cap G_{\alpha }$,那么便能选出若干$\alpha$,使得
$$K\subset V_{{\alpha }_1}\cup \cdots \cup V_{{\alpha }_n}$$
又因为$V_{\alpha }\subset G_{\alpha }$，因此
$$K\subset G_{{\alpha }_1}\cup \cdots \cup G_{{\alpha }_n}$$

2.34 定理：凡度量空间的紧子集都是闭集
证明：设$K$是度量空间$X$的紧子集。接着证明$K$的余集是开集
设$p\in X,p\notin K$。如果$q\in K$，令$V_q$和$W_q$分别是$p$和$q$的邻域，他们的半径小于$\frac{1}{2}d\left(p,q\right)$
因为$K$是紧，所以在$K$中有有限个多个点$q_1,q_2,\cdots ,q_n$使得
$$K\subset W_{q_1}\cup \cdots \cup W_{q_n}=W$$
令$V=V_{q_1}\cap \cdots \cap V_{V_{q_n}}$,那么$V$是$p$的邻域，并且$V\cap W=\varnothing$，因此$V\subset K^c$
也就是说$p$是$K^c$的内点，证毕

2.35 定理 凡紧集的闭子集都是紧集
证明：
设$F\subset K\subset X$，$F$是关于$X$是闭的，$K$关于$X$是紧的
令 { V α } \left\{ V_{\alpha} \right\} {Vα​}是$F$的开覆盖。令 Ω = { F c } ∪ { V α } \Omega = \left\{ F^c \right\} \cup \left\{ V_{\alpha} \right\} Ω={Fc}∪{Vα​}，$\Omega$是$K$的开覆盖
因为$K$是紧的，所以$\Omega$的一个有限子覆盖$\Phi$能覆盖$K$，从而也能覆盖$F$
如果$F^c$也是$\Phi$的成员，把它从$\Phi$里去掉，剩下的仍然是$K$的开覆盖。这就证明了 { V α } \left\{ V_{\alpha} \right\} {Vα​}的一个有限子组覆盖了$F$
推论：如果$F$是闭的，而$K$是紧的，那么$F\cap K$是紧的
证明：
$K$是紧的，从而$K$是闭得，于是$F\cap K$是闭的
$F\cap K\subset K$,从而$F\cap K$是紧的

2.36 定理 如果 { K α } \left\{ K_{\alpha} \right\} {Kα​}是度量空间$X$的一组紧子集，并且 { K α } \left\{ K_{\alpha} \right\} {Kα​}中任意有限个集的交都不是空集，那么$\cap K_{\alpha }$也不是空集
证明：
取定 { K α } \left\{ K_{\alpha} \right\} {Kα​}的一个集$K_1$，令$G_{\alpha }=K_{\alpha }^c$
假定$K_1$中没有同时属于每个$K_{\alpha }$的点，那么$G_{\alpha }$便形成$K_1$的一个开覆盖。因为$K_1$是紧的，所以有有限多个指标${\alpha }_1,\cdots ,{\alpha }_n$,使得$K_1\subset G_{{\alpha }_1}\cup \cdots \cup G_{{\alpha }_n}$,然而这意味着
$$K_1\cap K_{{\alpha }_1}\cap \cdots \cap K_{{\alpha }_n}=\varnothing$$
矛盾
推论: 设 { K n } \left\{ K_{n} \right\} {Kn​}是非空紧集的序列并且$K_n\supset K_{n+1}$,那么${\cap }_{n=1}^{\infty }{K}_n$是非空的

2.37 定理 设$E$是紧集$K$的无限子集，那么$E$在$K$中有极限点
证明：如果$K$里没有$E$的极限点，那么每个$q\in K$酱油一个邻域$V_q$，它最多含有$E$的一个点.
显然，没有 { V q } \left\{ V_{q} \right\} {Vq​}的有限子组能够覆盖$E$（毕竟你现在一个集合就一个点，无限个点可不得无限个集合）
这对于$K$也一样，因为$E\subset K$。这与$K$的紧性矛盾

2.38 定理 设 { I n } \left\{ I_{n} \right\} {In​}是${\mathbb{R}}^1$中的闭区间序列，并且$I_n\supset I_{n+1}$，那么${\cap }_{n=1}^{\infty }{I}_n$不是空集
证明：
设$I_n=\left[a_n,b_n\right]$，令$E$是一切$a_n$所构成的集。那么$E$是非空的且有上界$b_1$
令$x=\sup E$。如果$m,n\in {\mathbb{N}}_{+}$，那么
$$a_n\le a_{m+n}\le x\le b_{m+n}\le b_m$$
因此对于每个$m$，有$x\in I_m$

2.39 定理 设$k$是正整数。如果 { I n } \left\{ I_{n} \right\} {In​}是$k$-放个的序列，并且$I_n\supset I_{n+1}$，那么${\cap }_{n=1}^{\infty }{I}_n$不是空集
证明：
（其实拆成$k$个区间用一下定理2.38就出来了）
设$I_n$由一切
$$a_{n,j}\le x_j\le b_{n,j}$$
的点$\mathbf{x}$组成，令$I_{n,j}=\left[a_{n,j},b_{n,j}\right]$
由定理2.38，存在实数$x_j^{\ast }$，满足
$$a_{n,j}\le x_j^{\ast }\le b_{n,j}$$
对于每个$n$，有${\mathbf{x}}^{\ast }\in I_n$

2.40 定理 每个$k$方格是紧集
证明：令$I$是$k$-方格。令
$$\delta =\Vert \mathbf{a}-\mathbf{b}\Vert$$
当$\mathbf{x},\mathbf{y}\in I$,有$\Vert \mathbf{x}-\mathbf{y}\Vert \le \delta$

假定存在$I$的一个开覆盖 { G α } \left\{ G_{\alpha} \right\} {Gα​}，它不含$I$的任何有限子覆盖。令$c_j=\frac{a_j+b_j}{2}$，那么闭区间$\left[a_j,c_j\right]$和$\left[c_j,b_j\right]$确定$2^k$个$k$方格$Q_i$，显然$I={\cup }_{i=1}^{2^k}{Q}_i$
存在$I_1=Q_i$，不能被 { G α } \left\{ G_{\alpha} \right\} {Gα​}的任何有限子组覆盖。
再分$I_1$,并且继续分下去，我们得到一个序列 { I n } \left\{ I_{n} \right\} {In​},它具有以下性质
(a) $I\supset I_1\supset I_2\supset \cdots$
(b) $I_n$不能被 { G α } \left\{ G_{\alpha} \right\} {Gα​}的任何有限子组覆盖
© 如果$\mathbf{x},\mathbf{y}\in I_n$，那么$\Vert \mathbf{x}-\mathbf{y}\Vert \le 2^{-n}\delta$
存在一点${\mathbf{x}}^{\ast }$，它在每个$I_n$之内。对于某个$\alpha ,{\mathbf{x}}^{\ast }\in G_{\alpha }$
因为$G_{\alpha }$是开的，所以存在一个$r>0$，使得由$\Vert \mathbf{x}-\mathbf{y}\Vert <r$推出$\mathbf{y}\in G_{\alpha }$
如果$n$大到了出现$2^{-n}\delta <r$时（这样的$n$一定存在，否则将对一切正整数$n$，$2^n\le \frac{\delta }{r}$，由$\mathbb{R}$的阿基米德性，这是不可能的）因此©就得出$I_n\subset G_{\alpha }$，与(b)矛盾

下面定理中(a)和(b)的等价性就是又名的Heine-Borel定理
2.41 定理 如果${\mathbb{R}}^k$中一个集$E$具有下列三个性质之一，那么它具有其他两个性质
(a)$E$是闭且有界的
(b)$E$是紧的
©$E$的每个无限子集在$E$内有极限点
证明：
如果(a)成立，这时存在某个$k$-方格$I$使$E\subset I$，于是根据定理2.40和2.35(b)成立
由定理2.37，(b)可以推出©.接下来证明©推(a)

‌‌‌‌　　如果$E$不是有界的，那么$E$会有一些点${\mathbf{x}}_n$合于
$$\Vert {\mathbf{x}}_n\left|\right|>n$$
由这些$x_n$所组成的集$S$是一个无限集，并且显然在${\mathbb{R}}^k$中没有极限点，因而在$E$中没有极限点，因此$E$是有界的
‌‌‌‌　　如果$E$不是闭集，那么存在一点${\mathbf{x}}_0\in {\mathbb{R}}^k$，它是$E$的极限点，但是不在$E$内。对于$n=1,2,3.\cdots$，存在点$x_n\in E$，使得$\left|x_n-x_0\right|<\frac{1}{n}$.(这里不会选的点都一样，因为$n$越来越大)
令$S$是这些$x_n$所成的集。那么$S$是无限集（不然的话，$\left|x_n-x_0\right|$将对于无限个多个$n$，取一个固定的正值）。$S$以$x_0$为极限点，并且$S$在${\mathbb{R}}^k$中没有其他的极限点。事实上，如果$\mathbf{y}\in {\mathbb{R}}^k,\mathbf{y}\ne {\mathbf{x}}_0$。那么除了有限几个$n$以外，
$$\begin{array}{rl}\left|{\mathbf{x}}_{\mathbf{n}}-\mathbf{y}\right|& \ge \left|{\mathbf{x}}_0-\mathbf{y}\right|-\left|{\mathbf{x}}_n-{\mathbf{x}}_0\right|\\ & \ge \left|{\mathbf{x}}_0-\mathbf{y}\right|-\frac{1}{n}\\ & \ge \frac{1}{2}\left|{\mathbf{x}}_0-\mathbf{y}\right|\end{array}$$
若$r<\frac{1}{2}\left|{\mathbf{x}}_0-\mathbf{y}\right|$，那么$N_r\left(\mathbf{y}\right)$只有有限个$S$中的点（或者空集），这就证明了$\mathbf{y}$不是$S$的极限点
‌‌‌‌　　这样一来，$S$在$E$里没有极限点。因此，如果© 成立，那么$E$一定是闭集
‌‌‌‌　　在这一点上我们应当注意，在任何度量空间里(b)和©是等价的，然而一般来说，(a)不能推出(b)和©

2.42 定理(Weierstrass) ${\mathbb{R}}^k$中每个有界无限子集在${\mathbb{R}}^k$中由极限点
证明：所说的这个集$E$既然有界，必是一个$k$-方格$I\subset {\mathbb{R}}^k$的子集。
$I$是紧集，因此$E$在$I$里由极限点

完全集

2.43 定理 令$P$是${\mathbb{R}}^k$中的非空完全集，那么$P$是不可数的
证明：因为$P$有极限点，所以$P$是无限集。如果$P$可数，将$P$中的点记作${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots$，我们按下面的方式构造一个邻域序列 { V n } \left\{ V_{n} \right\} {Vn​}
‌‌‌‌　　令$V_1$是${\mathbf{x}}_1$的任意一个邻域。如果$V_1=\left\{\mathbf{y}\in {\mathbb{R}}^k:\left|\mathbf{y}-{\mathbf{x}}_1\right|<r\right\}$。$V_1$的闭包${\bar{V}}_1=\left\{\mathbf{y}\in {\mathbb{R}}^k:\left|\mathbf{y}-{\mathbf{x}}_1\right|\le r\right\}$
‌‌‌‌　　假定已经作出$V_n$，那么$V_n\cap P\ne \varnothing$。因为$P$的每个点都是$P$的极限点，所以存在一个邻域$V_{n+1}$，使得(i)${\bar{V}}_{n+1}\subset V_n$，(ii)${\mathbf{x}}_n\notin {\bar{V}}_{n+1}$，(iii)$V_{n+1}\cap P\ne \varnothing$，由(iii)来看，$V_{n+1}$满足归纳法的假设，因此，这种构造法可以继续进行。
‌‌‌‌　　令$K_n={\bar{V}}_n\cap P$。因为${\bar{V}}_n$是有界闭集，所以${\bar{V}}_n$是紧集。因为${\mathbf{x}}_n\notin K_{n+1}$，所以${\bigcap }_{i=1}^{\infty }{K}_n$没有$P$的点。因为$K_n\subset P$，这意味着${\bigcap }_{i=1}^{\infty }{K}_n=\varnothing$。然而由(iii)，每个$K_n\ne \varnothing$。并且由(i)，$K_n\supset K_{n+1}$；这与定理2.36的推论矛盾
推论 每个闭区间$\left[a,b\right]\left(a<b\right)$是不可数的，特别地，$\mathbb{R}$是不可数的

2.44 Cantor集 我们将要构造出的这个集表明，在${\mathbb{R}}^1$中存在不包含开区间的完全集
$E_0=\left[0,1\right]$,去掉开区间$\left(\frac{1}{3},\frac{2}{3}\right)$，并令
$$E_1=\left[0,\frac{1}{3}\right]\cup \left[\frac{2}{3},1\right]$$
将这两个闭区间都三等分，并去掉中间的那个开区间。令
$$E_2=\left[0,\frac{1}{9}\right]\cup \left[\frac{2}{9},\frac{3}{9}\right]\cup \left[\frac{6}{9},\frac{7}{9}\right]\cup \left[\frac{8}{9},1\right]$$
按照这个方式进行下去，就得到紧集$E_n$的一个序列，显然
(a)$E_1\supset E_2\supset \cdots$
(b)$E_n$是$2^n$个区间的并，每个闭区间的长度为$3^{-n}$
集
$$P=\bigcap _{n=1}^{\infty }{E}_n$$
叫做Cantor集。显然$P$是紧集。并且按照定理2.36表明，$P$不是空集
如果$k,m\in {\mathbb{N}}_{+}$，那么没有一个形式为
$$\left(\frac{3k+1}{3^m},\frac{3k+2}{3^m}\right)$$
的开区间能够和$P$有公共点。因为每个开区间$\left(\alpha ,\beta \right)$，一定含有上面这种开区间，只要
$$3^{-m}<\frac{\beta -\alpha }{6}$$
所以$P$不能含开区间
‌‌‌‌　　为了证明$P$是完全集，需要证明$P$没有孤立点。令$x\in P$，而$S$是包含$x$的任意一个开区间。令$I_n$是$E_n$中包含$x$的那个开区间，选择足够大的$n$，使得$I_n\subset S$。令$x_n$是$I_n$的那个不等于$x$的端点。
‌‌‌‌　　从构造$P$的方法知道$x_n\in P$，因此$x$是$P$的一个极限点，从而$P$是完备的。
‌‌‌‌　　Cantor集是一个测度为零的不可数集

连通集

2.45 定义 设$A,B$是度量空间$X$的两个子集。如果$A\cap \bar{B}$以及$\bar{A}\cap B$都是空集，即如果$A$的点不在$B$的闭包中，$B$的点也不在$A$的闭包中，就说$A$和$B$是分离的（seperated）
如果集$E\subset X$不是两个非空分离集的并，就说$E$是连通集（connected set）

2.46 评注 分离的两个集是不相交的，但是不相交的集不一定是分离集。$[0,1]$和$(1,2)$不是分离的。$(0,1)$和$(1,2)$是分离的

2.47 定理 实数轴${\mathbb{R}}^1$的子集$E$是连通的，当且仅当它有以下性质：如果$x\in E,y\in E$，并且$x<z<y$，那么$z\in E$
证明：
‌‌‌‌　　$E$是连通的。假设存在$x\in E,y\in E$以及某个$z\in \left(x,y\right)$而$z\notin E$，那么$E=A_z\cup B_z$，这里
$$A_z=E\cap \left(-\infty ,z\right),B_z=E\cap \left(z,\infty \right)$$
因为$x\in A_z,y\in B_z$，$A,B$都不为空。因为$A_z\subset \left(-\infty ,z\right),B_z\subset \left(z,\infty \right)$，他们是分离的。由此$E$不是连通的，矛盾
‌‌‌‌　　反过来，假设$E$不连通，那么，$E$就等于某两个不空分离集$A,B$的并，即$E=A\cup B$.
取$x\in A,y\in B$，不妨假设$x<y$，定义
$$z=\sup \left(A\cap \left[x,y\right]\right)$$
根据定理2.28，$z\in \bar{A}$；因此$z\notin B$，特别有$x\le z<y$
‌‌‌‌　　如果$z\notin A$，那么$x<z<y$，而$z\notin E$，矛盾
‌‌‌‌　　如果$z\in A$，那么$z\notin \bar{B}$，因此存在$z_1$使得$z<z_1<y$且$z_1\notin B$.于是$x<z_1<y$而$z_1\notin E$,矛盾