引言:快速排序作为一种非常经典且高效的排序算法,无论是工作还是面试中广泛用到,作为一种分治思想,需要熟悉递归思想。下面来讲讲快速排序的实现和改进。
老规矩,先用图解来理解一下:(这里使用快速排序中的“挖坑法”)
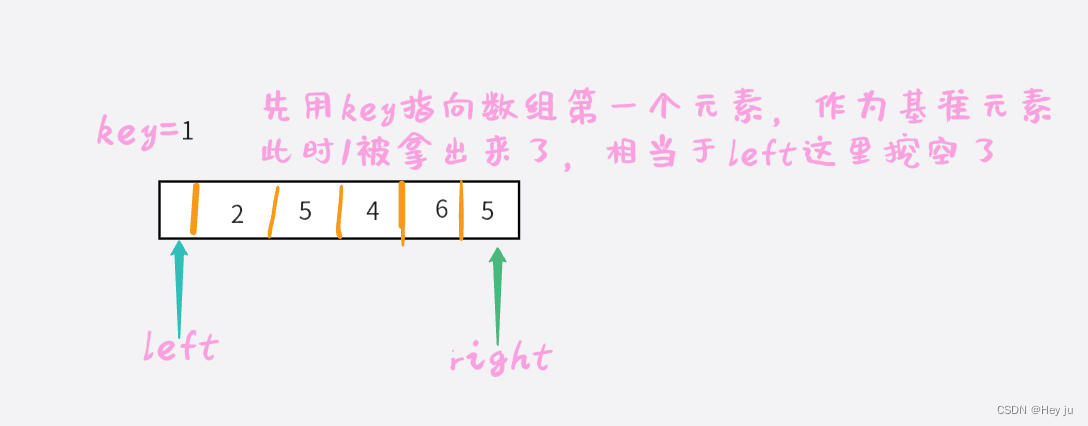
笔误:下面这个图right是--的!

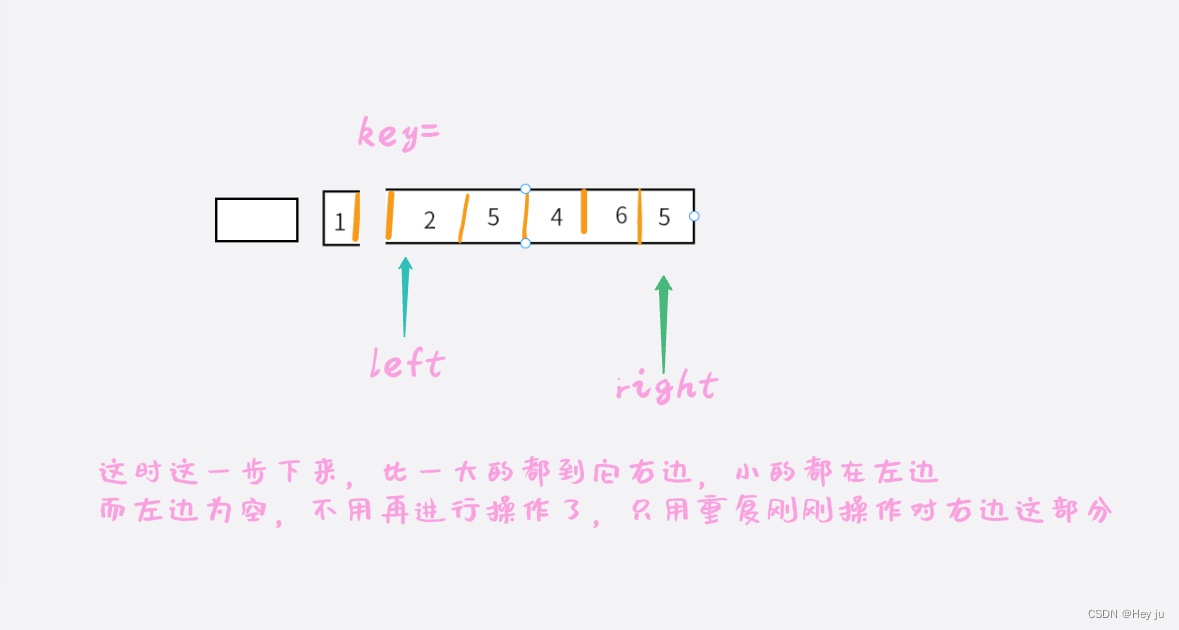
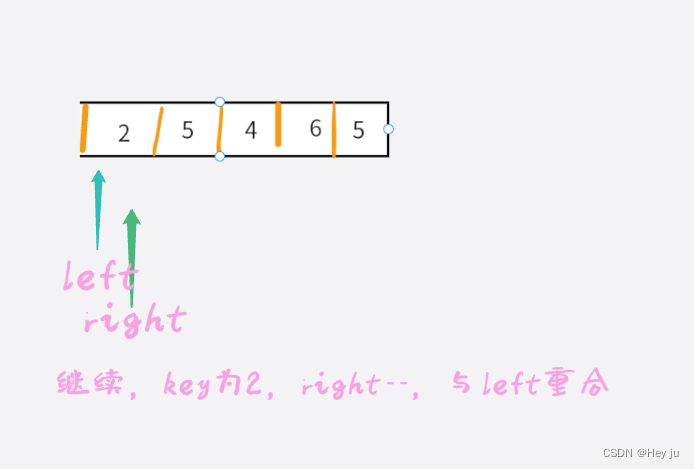

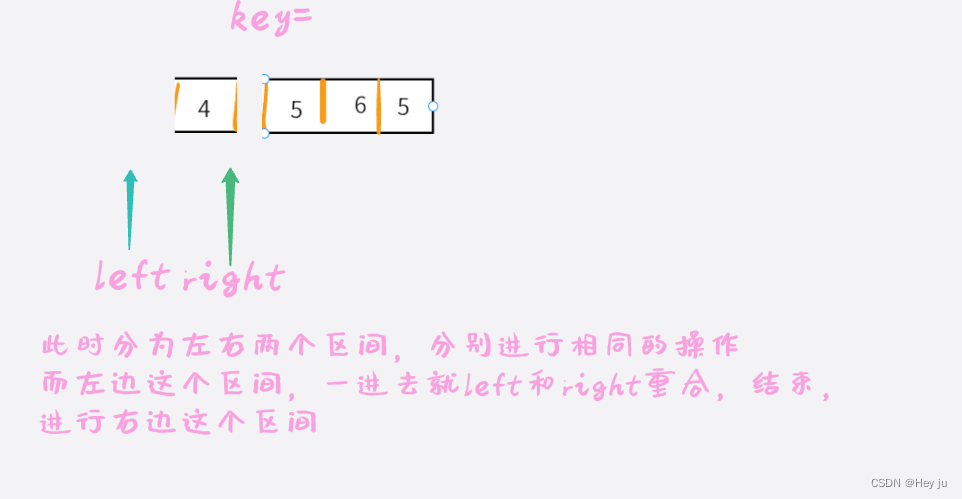 以此往复
以此往复
下面是代码:
void dfs_quick_sort(int* arry, int left, int right) {if ((right - left) <= 0) return;//添加一个三数取中的操作int key = arry[left];int end = right;int begin = left;while (left < right) {while (left < right && arry[right] >= key) {right--;}arry[left] = arry[right];while (left < right && arry[left] <= key) {left++;}arry[right] = arry[left];}arry[right] = key;dfs_quick_sort(arry,begin, left - 1);dfs_quick_sort(arry,right + 1, end);
}
//挖坑法
void quick_sort(int* arry, int size) {assert(arry);dfs_quick_sort(arry, 0, size - 1);
}测试代码:
void test_quick_sort(int* arry, int size) {Printf(arry, size);quick_sort(arry, size);Printf(arry, size);
}
int main() {int arry[] = { 2,3,1,6,21,78,11,36,11,11,9 };int len = sizeof(arry) / sizeof(arry[0]);//test_insertion_sort(arry, len);//est_shell_sort(arry, len);//test_select_sort(arry, len);//test_heap_sort(arry, len);//test_bubble_sort(arry, len);test_quick_sort(arry, len);return 0;
}MORE:试想如果刚刚演示的图中,一开始取到的不是1,而是5,是不是步骤会少很多,因为如果拿到的是排好序后的中间数,这个数左边是比他小的,右边是比他大的,每次这样,相当于每次都二分,这样向下递归层数就是logN,而如果每次拿到的key是最大或最小的数,第一次操作完还剩n-1个,第二次还剩n-2....。层数为n层,时间复杂度为N^2。
所以我们要尽量选到一个靠近排序好的中间的数,不要选到最大或最小的数为key。
下面将代码进行改进:(取最左边和最右边和中间三个值中的中间数)
int mid_quick_number(int* arry, int left, int right) {int mid = left + (right - left >> 1);//去中间数防止普通求中间数溢出问题if (arry[mid] > arry[left]) {if (arry[right] > arry[mid]) {mid = mid;}else if(arry[right]>arry[left]){mid = right;}else {mid = left;}}else {if (arry[right] < arry[mid]) {mid = mid;}else if (arry[right] > arry[left]) {mid = left;}else {mid = right;}}return mid;
}
void dfs_quick_sort(int* arry, int left, int right) {if ((right - left) <= 0) return;//添加一个三数取中的操作int mid = mid_quick_number(arry, left, right);swap(arry + mid, arry+left);int key = arry[left];int end = right;int begin = left;while (left < right) {while (left < right && arry[right] >= key) {right--;}arry[left] = arry[right];while (left < right && arry[left] <= key) {left++;}arry[right] = arry[left];}arry[right] = key;dfs_quick_sort(arry,begin, left - 1);dfs_quick_sort(arry,right + 1, end);
}
//挖坑法
void quick_sort(int* arry, int size) {assert(arry);dfs_quick_sort(arry, 0, size - 1);
}
(含MATLAB代码))



背景无限滚屏效果如何实现)


![[架构之路-231]:计算机硬件与体系结构 - 性能评估汇总,性能优化加速比](http://pic.xiahunao.cn/[架构之路-231]:计算机硬件与体系结构 - 性能评估汇总,性能优化加速比)
)
)



是什么?定量结构-性质关系(QSPR)是什么?)

)


)