⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️
🐴作者:秋无之地🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。
🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、留言💬、关注🤝,关注必回关
上一篇文章已经跟大家介绍过《EM聚类(下):用EM算法对王者荣耀英雄进行划分》,相信大家对EM聚类(下)都有一个基本的认识。下面我讲一下,关联规则挖掘(上):数据分析 | 数据挖掘 | 十大算法之一
一、关联规则挖掘背景
关联规则这个概念,最早是由 Agrawal 等人在 1993 年提出的。在 1994 年 Agrawal 等人又提出了基于关联规则的 Apriori 算法,至今 Apriori 仍是关联规则挖掘的重要算法。
关联规则挖掘可以让我们从数据集中发现项与项(item 与 item)之间的关系,它在我们的生活中有很多应用场景,“购物篮分析”就是一个常见的场景,这个场景可以从消费者交易记录中发掘商品与商品之间的关联关系,进而通过商品捆绑销售或者相关推荐的方式带来更多的销售量。所以说,关联规则挖掘是个非常有用的技术。
在今天的内容中,希望你能带着问题,和我一起来搞懂以下几个知识点:
- 搞懂关联规则中的几个重要概念:支持度、置信度、提升度;
- Apriori 算法的工作原理;
- 在实际工作中,我们该如何进行关联规则挖掘。
二、搞懂关联规则中的几个概念
我举一个超市购物的例子,下面是几名客户购买的商品列表:
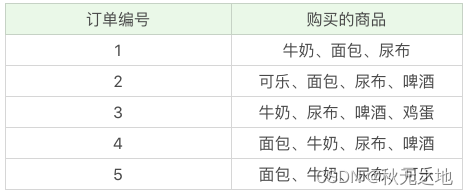
1、支持度
支持度是个百分比,它指的是某个商品组合出现的次数与总次数之间的比例。支持度越高,代表这个组合出现的频率越大。
在这个例子中,我们能看到“牛奶”出现了 4 次,那么这 5 笔订单中“牛奶”的支持度就是 4/5=0.8。
同样“牛奶 + 面包”出现了 3 次,那么这 5 笔订单中“牛奶 + 面包”的支持度就是 3/5=0.6。
2、置信度
它指的就是当你购买了商品 A,会有多大的概率购买商品 B,在上面这个例子中:
置信度(牛奶→啤酒)=2/4=0.5,代表如果你购买了牛奶,有多大的概率会购买啤酒?
置信度(啤酒→牛奶)=2/3=0.67,代表如果你购买了啤酒,有多大的概率会购买牛奶?
我们能看到,在 4 次购买了牛奶的情况下,有 2 次购买了啤酒,所以置信度 (牛奶→啤酒)=0.5,而在 3 次购买啤酒的情况下,有 2 次购买了牛奶,所以置信度(啤酒→牛奶)=0.67。
所以说置信度是个条件概念,就是说在 A 发生的情况下,B 发生的概率是多少。
3、提升度
我们在做商品推荐的时候,重点考虑的是提升度,因为提升度代表的是“商品 A 的出现,对商品 B 的出现概率提升的”程度。
还是看上面的例子,如果我们单纯看置信度 (可乐→尿布)=1,也就是说可乐出现的时候,用户都会购买尿布,那么当用户购买可乐的时候,我们就需要推荐尿布么?
实际上,就算用户不购买可乐,也会直接购买尿布的,所以用户是否购买可乐,对尿布的提升作用并不大。我们可以用下面的公式来计算商品 A 对商品 B 的提升度:
提升度 (A→B)= 置信度 (A→B)/ 支持度 (B)
这个公式是用来衡量 A 出现的情况下,是否会对 B 出现的概率有所提升。
所以提升度有三种可能:
- 提升度 (A→B)>1:代表有提升;
- 提升度 (A→B)=1:代表有没有提升,也没有下降;
- 提升度 (A→B)<1:代表有下降。
三、Apriori 的工作原理
明白了关联规则中支持度、置信度和提升度这几个重要概念,我们来看下 Apriori 算法是如何工作的。
首先我们把上面案例中的商品用 ID 来代表,牛奶、面包、尿布、可乐、啤酒、鸡蛋的商品 ID 分别设置为 1-6,上面的数据表可以变为:
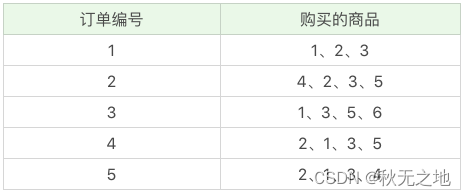
Apriori 算法其实就是查找频繁项集 (frequent itemset) 的过程,所以首先我们需要定义什么是频繁项集。
频繁项集就是支持度大于等于最小支持度 (Min Support) 阈值的项集,所以小于最小值支持度的项目就是非频繁项集,而大于等于最小支持度的项集就是频繁项集。
项集这个概念,英文叫做 itemset,它可以是单个的商品,也可以是商品的组合。我们再来看下这个例子,假设我随机指定最小支持度是 50%,也就是 0.5。
我们来看下 Apriori 算法是如何运算的。
首先,我们先计算单个商品的支持度,也就是得到 K=1 项的支持度:
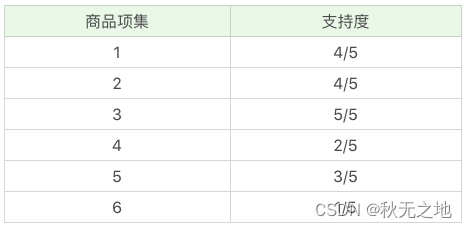
因为最小支持度是 0.5,所以你能看到商品 4、6 是不符合最小支持度的,不属于频繁项集,于是经过筛选商品的频繁项集就变成:
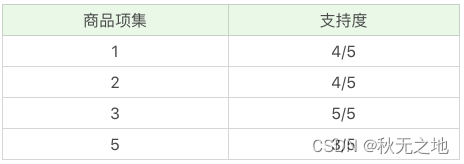
在这个基础上,我们将商品两两组合,得到 k=2 项的支持度:
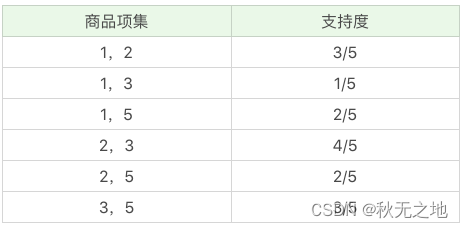
我们再筛掉小于最小值支持度的商品组合,可以得到:
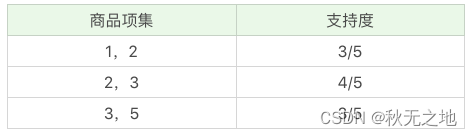
我们再将商品进行 K=3 项的商品组合,可以得到:
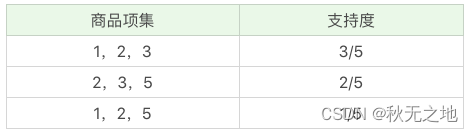
再筛掉小于最小值支持度的商品组合,可以得到:

通过上面这个过程,我们可以得到 K=3 项的频繁项集{1,2,3},也就是{牛奶、面包、尿布}的组合。
到这里,你已经和我模拟了一遍整个 Apriori 算法的流程,下面我来给你总结下 Apriori 算法的递归流程:
- K=1,计算 K 项集的支持度;
- 筛选掉小于最小支持度的项集;
- 如果项集为空,则对应 K-1 项集的结果为最终结果。
否则 K=K+1,重复 1-3 步。
四、Apriori 的改进算法:FP-Growth 算法
我们刚完成了 Apriori 算法的模拟,你能看到 Apriori 在计算的过程中有以下几个缺点:
- 可能产生大量的候选集。因为采用排列组合的方式,把可能的项集都组合出来了;
- 每次计算都需要重新扫描数据集,来计算每个项集的支持度。
所以 Apriori 算法会浪费很多计算空间和计算时间,为此人们提出了 FP-Growth 算法,它的特点是:
- 创建了一棵 FP 树来存储频繁项集。在创建前对不满足最小支持度的项进行删除,减少了存储空间。我稍后会讲解如何构造一棵 FP 树;
- 整个生成过程只遍历数据集 2 次,大大减少了计算量。
所以在实际工作中,我们常用 FP-Growth 来做频繁项集的挖掘,下面我给你简述下 FP-Growth 的原理。
1、创建项头表(item header table)
创建项头表的作用是为 FP 构建及频繁项集挖掘提供索引。
这一步的流程是先扫描一遍数据集,对于满足最小支持度的单个项(K=1 项集)按照支持度从高到低进行排序,这个过程中删除了不满足最小支持度的项。
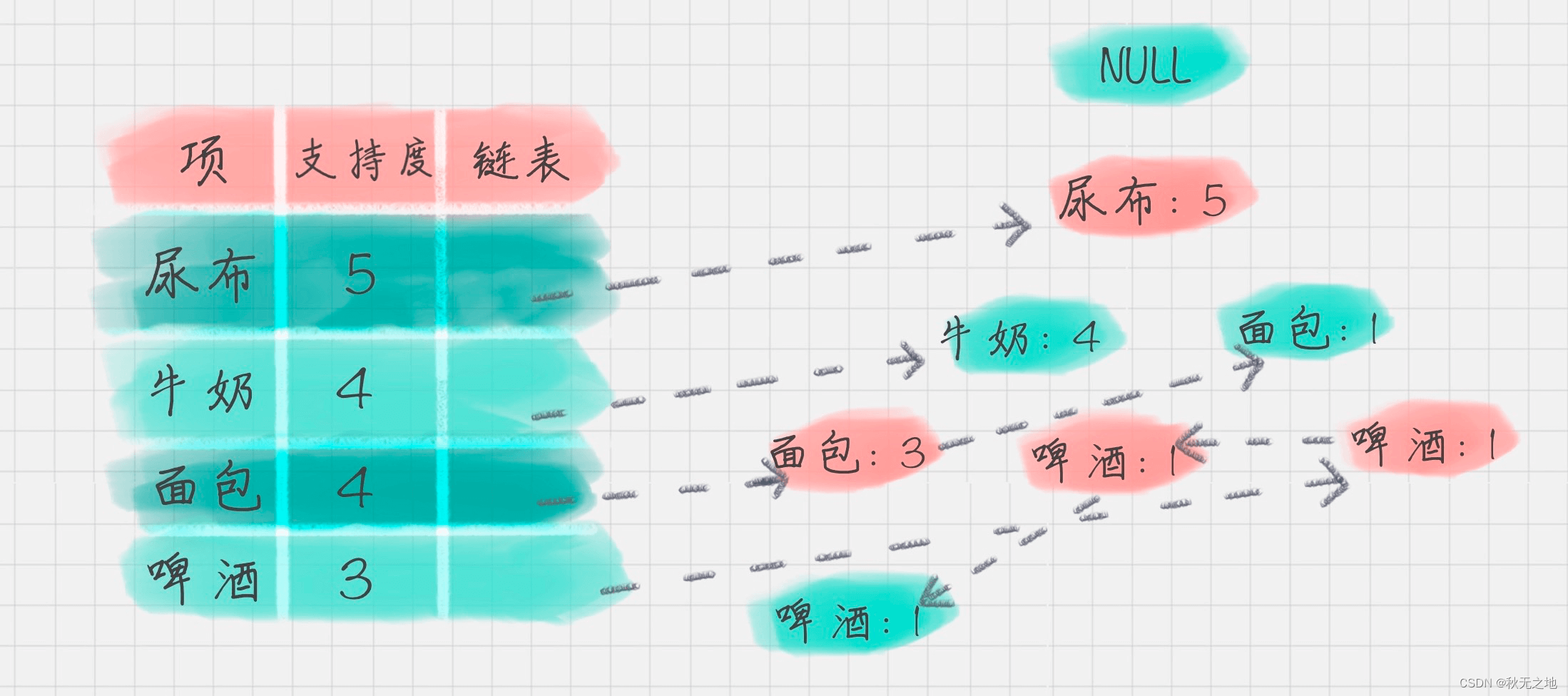
项头表包括了项目、支持度,以及该项在 FP 树中的链表。初始的时候链表为空。
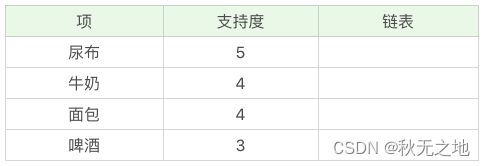
2、构造 FP 树
FP 树的根节点记为 NULL 节点。
整个流程是需要再次扫描数据集,对于每一条数据,按照支持度从高到低的顺序进行创建节点(也就是第一步中项头表中的排序结果),节点如果存在就将计数 count+1,如果不存在就进行创建。同时在创建的过程中,需要更新项头表的链表。
3、通过 FP 树挖掘频繁项集
到这里,我们就得到了一个存储频繁项集的 FP 树,以及一个项头表。我们可以通过项头表来挖掘出每个频繁项集。
具体的操作会用到一个概念,叫“条件模式基”,它指的是以要挖掘的节点为叶子节点,自底向上求出 FP 子树,然后将 FP 子树的祖先节点设置为叶子节点之和。
我以“啤酒”的节点为例,从 FP 树中可以得到一棵 FP 子树,将祖先节点的支持度记为叶子节点之和,得到:
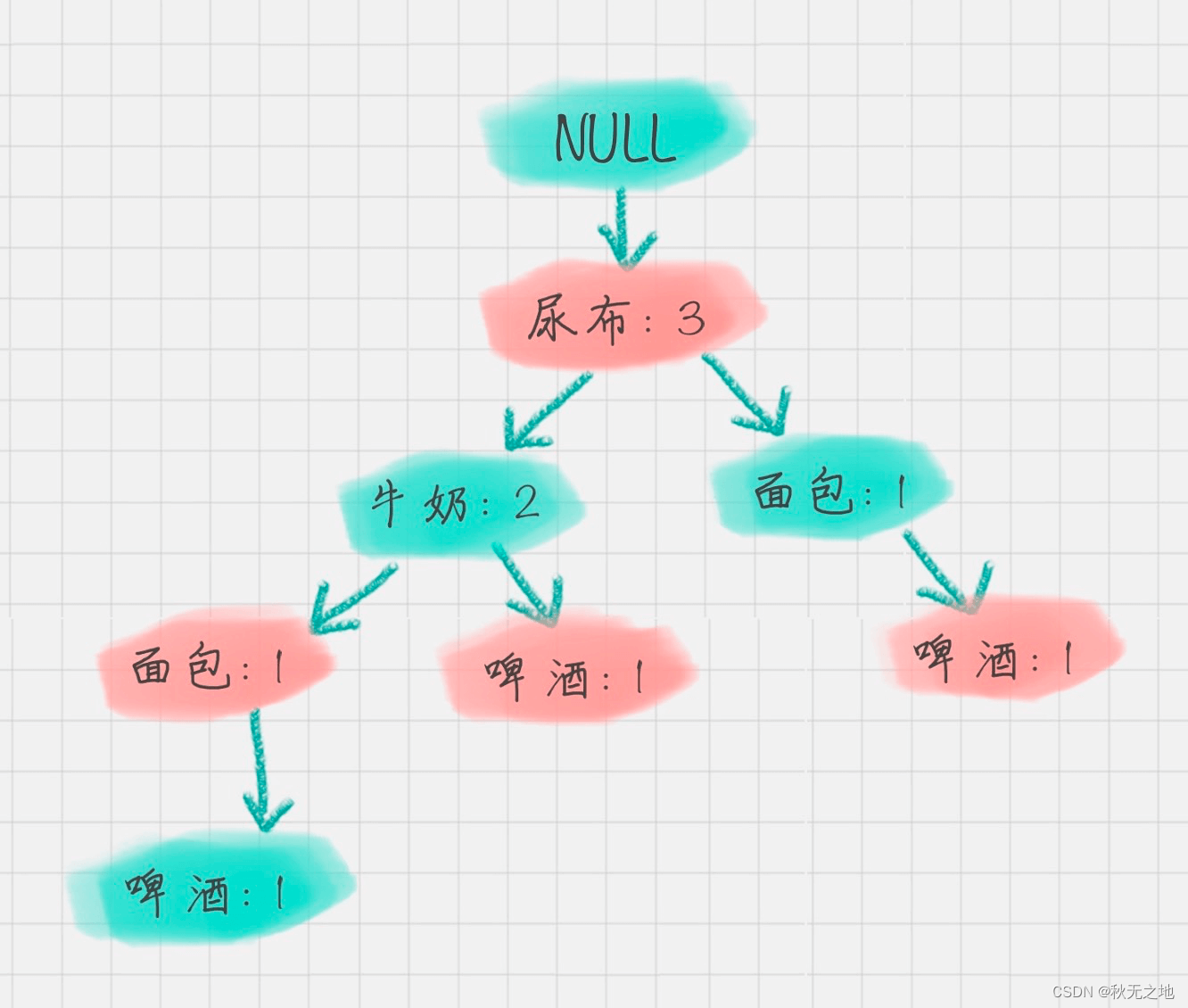
你能看出来,相比于原来的 FP 树,尿布和牛奶的频繁项集数减少了。这是因为我们求得的是以“啤酒”为节点的 FP 子树,也就是说,在频繁项集中一定要含有“啤酒”这个项。你可以再看下原始的数据,其中订单 1{牛奶、面包、尿布}和订单 5{牛奶、面包、尿布、可乐}并不存在“啤酒”这个项,所以针对订单 1,尿布→牛奶→面包这个项集就会从 FP 树中去掉,针对订单 5 也包括了尿布→牛奶→面包这个项集也会从 FP 树中去掉,所以你能看到以“啤酒”为节点的 FP 子树,尿布、牛奶、面包项集上的计数比原来少了 2。
条件模式基不包括“啤酒”节点,而且祖先节点如果小于最小支持度就会被剪枝,所以“啤酒”的条件模式基为空。
同理,我们可以求得“面包”的条件模式基为:

所以可以求得面包的频繁项集为{尿布,面包},{尿布,牛奶,面包}。同样,我们还可以求得牛奶,尿布的频繁项集,这里就不再计算展示。
五、总结
今天我给你讲了 Apriori 算法,它是在“购物篮分析”中常用的关联规则挖掘算法,在 Apriori 算法中你最主要是需要明白支持度、置信度、提升度这几个概念,以及 Apriori 迭代计算频繁项集的工作流程。
Apriori 算法在实际工作中需要对数据集扫描多次,会消耗大量的计算时间,所以在 2000 年 FP-Growth 算法被提出来,它只需要扫描两次数据集即可以完成关联规则的挖掘。FP-Growth 算法最主要的贡献就是提出了 FP 树和项头表,通过 FP 树减少了频繁项集的存储以及计算时间。
当然 Apriori 的改进算法除了 FP-Growth 算法以外,还有 CBA 算法、GSP 算法,这里就不进行介绍。
你能发现一种新理论的提出,往往是先从最原始的概念出发,提出一种新的方法。原始概念最接近人们模拟的过程,但往往会存在空间和时间复杂度过高的情况。所以后面其他人会对这个方法做改进型的创新,重点是在空间和时间复杂度上进行降维,比如采用新型的数据结构。你能看出树在存储和检索中是一个非常好用的数据结构。
版权声明
本文章版权归作者所有,未经作者允许禁止任何转载、采集,作者保留一切追究的权利。

![[C国演义] 第十三章](http://pic.xiahunao.cn/[C国演义] 第十三章)











)
)

)


