java - 七大比较排序

前言

本篇介绍了七大比较排序，直接插入排序，希尔排序，冒泡排序，堆排序，选择排序，快速排序，归并排序，一些简单思想+代码实现，如有错误，请在评论区指正，让我们一起交流，共同进步！

文章目录

前言
1. 直接插入排序
2. 希尔排序
3. 冒泡排序
4. 堆排序 - 基于完全二叉树
5. 选择排序
6 快速排序:
- 6.2 非递归快排
7. 归并排序
总结

本文开始

1. 直接插入排序

思路 : 一组数据, 当插入下标为i时的数据, 比较前面i-1个数据, 如果前面i-1个数据中，有数据大于插入为i位置下标的数据, i-1位置数据, 向后移动, 直至i-1个数据中没有小于i下标的值, 再将i下标的值插入j+1位置;
时间复杂度: O(N^2)
空间复杂度: O(1)
稳定性: 稳定
直接插入代码实现:

 public static void insertSort(int[] array) {//默认第一个有序不用排序, 从第二个开始排序for (int i = 1; i < array.length; i++) {int tmp = array[i];//作为判断标准,作为插入元素int j = i-1; //循环完,还需要使用到j下标, 所以拿出来定义for (; j >= 0; j--) {//判断tmp 是否 大于下标为j的元素if(array[j] > tmp) {//小于就前移一位array[ j+1] = array[ j ];}else {//插入值大于插入值前面的元素. 直接跳出//array[ j+1 ] = tmp;break;}}//比较完后,需要将插入值放到j+1位置array[j+1] = tmp;}}

2. 希尔排序

思想: 希尔排序, 直接插入排序的优化版本; 每组分组, 组数任意,这再进行排序(插入排序); 这里可以将数据除2依次分组;
数据分组不一定是相邻的,假设10个元素分5组,每组两个元素,在5位置的元素组数减5就是0位置,就是跟5一组的另一个元素;
以上可得到, 一个位置加减组数,可以得到一组的另外元素位置
平均时间复杂度: O(n^1.3)
空间复杂度: O(1)

希尔排序代码实现:

public static void shellSort(int[] array) {int gap = array.length;//初始化组数, 每个元素为一组,在除2分组while (gap > 1) {//shell排序shell(array,gap);//分组gap /= 2;}//第一次gap越界没有排, 此时以整体为一组,进行排序shell(array,gap);}public static void shell(int[] array,int gap) {//gap => 分几组的组数// 从第gap个开始排序for (int i = gap; i < array.length; i++) {int tmp = array[i];//作为判断标准,作为插入元素int j = i-gap; //循环完,还需要使用到j下标, 所以拿出来定义for (; j >= 0; j--) {//判断tmp 是否 大于下标为j的元素if(array[j] > tmp) {//小于就前移gap位array[j+gap] = array[j];}else {//插入值大于插入值前面的元素. 直接跳出break;}}//比较完后,需要将插入值放到j+1位置array[j+gap] = tmp;}}

3. 冒泡排序

思路: 升序为例,遍历数组, 比较两个相邻的值, 如果左位置大于右位置,就交换两个的位置, 一直比较数组结束;
时间复杂度: O(n^2)
空间复杂度: O(1)
稳定性: 稳定

冒泡排序优化实现 :
定义一个标志,某趟排序标志没有改变, 证明数组已经有序,不需要继续排序了,直接跳出即可;
发现每趟冒泡排序都会确定一个位置, 让每趟排序少1次比较;

public static void bubbleSort(int[] array) {//arrat.length个元素, 跑arrat.length-1趟//定义一个标志,某趟排序,标志没有改变, 证明数组已经有序,不需要继续排序了,直接跳出即可boolean flag = false; for (int i = 0; i < array.length - 1; i++) {for (int j = 0; j < array.length - 1 - i; j++) {if(array[j] > array[j+1]) {//交换swap(array,j,j+1);flag = true;}}if(flag == false) {break;}}}

4. 堆排序 - 基于完全二叉树

思路: 创建一个堆, 以大根堆为例, 要获取升序数组,只知道堆顶是最大,不知道左右孩子谁大, 需要堆排;
将堆顶与尾元素交换, 再向下调整为大根堆, 使尾元素下标-1, 循环执行此过程直至尾元素减为0;
时间复杂度: O(n*logn)
空间复杂度: O(logn)
稳定性: 不稳定

堆排序代码实现:

 public static void heapSort(int[] array) {//堆排先有堆,建立一个大根堆creatHeap(array);//大根堆的左右不能确定谁大谁小,所以需要堆排int end = array.length-1;while (end > 0) {//首尾元素交换swap(array,0,end);//此时保持大根堆,需要重新向下调整shiftDown(array,0,end);//排好最后一个位置, 最后一个位置有序,数组减1排下一个,第二大的就可以放到倒数第二,依次类推直到end结束//最后层序遍历,可以获取升序数组end--;}}//建堆(基于完全二叉树): 从最后一颗子树开始,使用向下调整(父节点位置向下移动到子节点位置)private static void creatHeap(int[] array) {//父节点下标 = ( 孩子节点下标 - 1 ) / 2for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(array,parent,array.length);}}//向下调整需要获取子节点位置, 所以给了父节点, 根据二叉树规则得到子节点下标,// 得到子节点下标,需要保证它不越界,// 通过观察每个子节点最大都不会超过数组长度, 所以给一个通用的数组长度即可private static void shiftDown(int[] array, int parent, int end) {//确定孩子节点int child = 2 * parent + 1;//必须有左孩子，保证孩子节点不越界while (child < end) {//左右孩子谁大，右孩子大则更新右孩子节点下标，否则不更新if(child + 1 < end && array[child] < array[child + 1]) {child++;//下标+1表示到了右孩子下标}//比较父子节点大小if(array[child] > array[parent]) {swap(array,child,parent);//更新父子节点位置，向下进行调整的，父子节点都是向下的parent = child;child = 2 * parent + 1;}else {break;//孩子小于父亲这棵树就不用换}}}

5. 选择排序

**思路①: 遍历数组, 第一个 i 位置有序,从i+1位置开始到数组结束(待排序位置), 寻找最小值下标, 提前定义变量记录最小值下标位置, 最小值不是一次就可以找到的, 可能需要不断更新需要记录; 找到之后交换最小值位置与 i 位置元素, 之后一次i++,重复上述操作即可;
思路②:
定义两个下标left, right表示每次遍历的范围，使用 i 遍历数组（数组范围[left+1,right]）；
循环找最大最小值下标maxIndex,minIndex,当left < right 时,找到两个下标, 分别进行交换（交换最小值与left位置，最大值与right交换）；
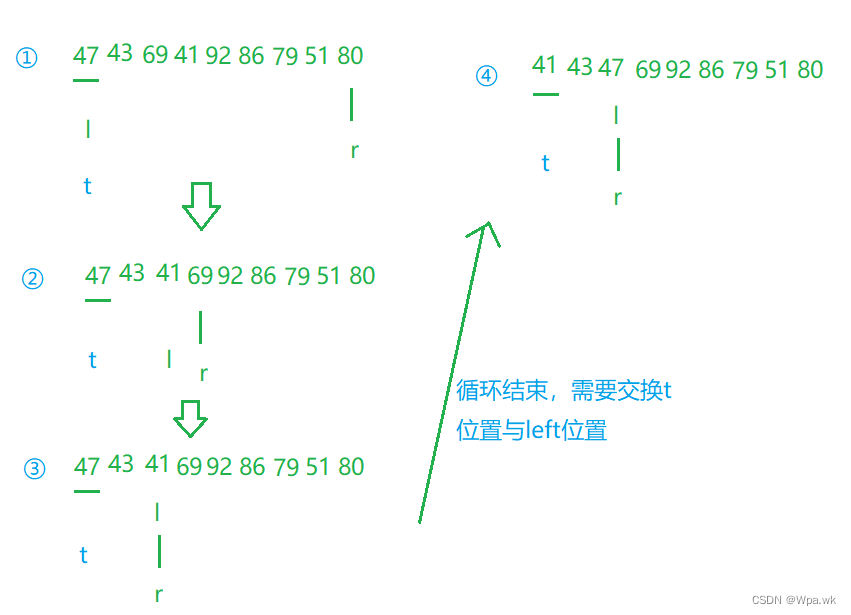
特殊情况：交换最小值与左下标, 交换后会遇到特殊情况最大值刚好位于left位置, 交换最小值后,最大值正好跑到最小值位置, 此时需要更新最大值位置; **
特殊情况如图: left位置与maxIndex位置一致时产生的问题

时间复杂度: O(n^2)
空间复杂度: O(1)
稳定性: 不稳定

选择排序代码1实现:

public static void selectSort(int[] array) {//遍历数组for (int i = 0; i < array.length; i++) {int minIndex = i;//在剩余待排序序列中找到最小的, 如果找不到直接下一个for (int j = i + 1; j < array.length; j++) {if(array[j] <  array[minIndex]) {//更改最小值下标minIndex = j;}}//找到最小值与起始位置交换, 每次i位置就为起始位置, 在剩余length-i位置中找比i位置小的元素,找到交换//直到数组找完 i > lengthint tmp = array[i];array[i] = array[minIndex];array[minIndex] = tmp;}}

选择排序代码2实现:

    public static void selectSort2(int[] array) {int left = 0;int right = array.length - 1;while (left < right) {//定义两个存储下标int minIndex = left;int maxIndex = left;//从待排序序列中找, 第一个认为有序, 找到最大最小值位置for (int i = left + 1; i < array.length; i++) {if(array[i] < array[minIndex]) {minIndex = i;}if(array[i] > array[maxIndex]) {maxIndex = i;}}//交换, 最小值换到左边, 最大值换到右边swap(array,left,minIndex);//存在特殊情况最大值刚好位于left位置, 交换最小值后,最大值正好跑到最小值位置// 此时需要更新最大值位置if(maxIndex == left) {maxIndex = minIndex;}//在交换最大值位置swap(array,right,maxIndex);left++;right--;}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}

6 快速排序:

思路: 快排递归是一样的,只是使用的找基准值下标的方法不同;
①挖坑法找基准值下标思路: 每次以第一个为基准定义为tmp(left位置), 先从数组右边开始找到大于tmp的数就将它放入left位置, 再从左边找到小于tmp的数,将他放到right位置, 直到left == right相遇时, tmp再放到left位置, 此时它的位置就是基准值位置;
② hoare法: 先记录最左边下标位置t, 循环结束后还需要交换t位置与新的left位置;
以第一个为基准值, 先从右边找到比基准值小的下标, 从左边找到比基准值大的下标, 再交换二者元素,依次交换直至left > right 循环结束;
好的情况:
时间复杂度: O(n*logn)
空间复杂度: O(logn)
坏蛋情况:
时间复杂度: O(n^2)
空间复杂度: O(n)
稳定性: 不稳定

快排代码: 基准值左边全部小于基准值, 基准值右边全部大于基准值,
patition方法能返回基准值下标, 再返还基准值下标前,代码已经完成排序操作了;

public void quickSort(int[] array) {quick(array,0,array.length-1);}private void quick(int[] array, int start, int end) {//判断越界if(start >= end) {return;}//基准值: 它的左边小于基准值,右边大于基准值;//获取下一次基准值下标,依次为界,将数组分为两个子序列//左右两边重复次过程int index = patition(array,start,end);//左右两边快排quick(array,start,index - 1);quick(array,index + 1,end);}//挖坑法 -private int patition(int[] array, int left, int right) {//获取第一个为基准值,一个数组的最左边int tmp = array[left];//遍历数组while (left < right) {//先遍历右边找到比基准值小的//从最右边往左边找, 如果都是小于第一个的值, 会越界需要判断while (left < right && array[right] > tmp) {right--;}//找到小的就放到左边array[left] = array[right];while (left < right && array[left] < tmp) {left++;}//左边找到大的就放到右边array[right] = array[left];}array[left] = tmp;//左右相遇时,此下标就是下一次分割数组的位置return left;}

**快排方法2:

    private int patition2(int[] array, int left, int right) {//获取第一个为基准值,一个数组的最左边int tmp = array[left];int t = left;//遍历数组while (left < right) {//先遍历右边找到比基准值小的//从最右边往左边找, 如果都是小于第一个的值, 会越界需要判断 => 逆序情况while (left < right && array[right] > tmp) {right--;}//从最左边往右边找, 如果都是大于第一个的值, 会越界需要判断 => 升序情况while (left < right && array[left] < tmp) {left++;}//交换左右下标值swap(array,left,right);}swap(array,t,left);//左右相遇时,此下标就是下一次分割数组的位置return left;}

hoare法模拟图示
交换全过程

快排代码优化:
优化1: 三数取中法, 在数组最左边,中间,最右边,比较获取中间的值下标, 与数组第一个元素交换;
patition每次会返回基准值下标, 为了让基准值在数组中间,均分数组
基准值分割数组,不一定是均等分割,这样排序速度就会减慢
优化2:减少递归次数, 排序到最后会趋向大部分有序, 对于大部分有序直接插入排序是最快的

		//优化2:if(end - start + 1 < 10) {insertSort(array,start,end);return;}//优化1: 尽量让基准值为于每次数组中间,均分数组能加快排序速度int midTree = minTree(array,start,end);//在最左边,中间,最右边,获取中间的值下标, 与数组第一个元素交换swap(array,midTree,start);

插入排序:

private void insertSort(int[] array, int start, int end) {for (int i = start + 1; i <= end; i++) {//从第二个开始,记录此时值int tmp = array[i];int j = i-1;for (; j >= start ; j--) {//数组中值大于 tmp j位置值前移1if(array[j] > tmp) {array[j+1] = array[j];}else {//前面的已经排行序了, 如果小于tmp直接跳出就行,不要看前面的了break;}}array[j] = tmp;}}

6.2 非递归快排

非递归思想:
第一次数组前后下标已知(0,array.length-1),从第二次开始使用栈;
求的基准值下标,根据基准值分割数组获取子数组;
判断获得的子数组元素是否大于1,大于1才让数组或子数组左右下标,放入栈中; 栈不为空,弹出栈中元素,进行快排patition方法(跟递归方法中的patition一样,这里就不写了)直到栈中元素为空

 public void quickSort2(int[] array) {//Deque实现的顺序栈Deque<Integer> stack = new ArrayDeque<>();//获取数组的前后下标int left = 0;int right = array.length - 1;//找基准值int pivot = patition(array,left,right);//保证基准值左边至少有一位数if(pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//保证基准值右边至少有1个元素if(pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}while (!stack.isEmpty()) {//先弹出右下标,再弹出左下标right = stack.pop();left = stack.pop();pivot = patition(array,left,right);//求新的基准值下标//保证基准值左边至少有一位数if(pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//保证基准值右边至少有1个元素if(pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}}//跳出循环, 再也没有子数组时,快排完毕;}

7. 归并排序

7.1 归并排序递归实现:
归并思想:
分治法: 先分,使用递归,将数组分为最小单位1, 再合并看自己要求,这里按升序为例, 合并两个数组,需定义一个新数组,数组1与数组2比较大小, 谁小谁先放入新数组, 可能两数组长度不一样, 长的数组的剩余元素直接放入新数组即可, 最后再将新数组组放到旧数组即可;

归并时间复杂度: O(n*logn)
空间复杂度: O(n)
稳定性: 稳定
归并排序实现代码:

public void mergeSort(int[] array) {mergeSortChild(array,0,array.length-1);}public void mergeSortChild(int[] array,int left,int right) {//防止越界,需要判断//当left == right: 说明递归结束if(left >= right) {return;}//找到中间下标,从而拆分数组int mid = (left + right) / 2;//拆分左边mergeSortChild(array,left,mid);//拆分右边mergeSortChild(array,mid + 1,right);//合并merge(array,left,right,mid);}//升序为例public void merge(int[] array, int left, int right, int mid) {//比较数组,需要遍历下标int s1 = left;int s2 = mid + 1;//数组2的开始下标//创建一个新数组,存放排好序的数组int[] tmp = new int[right - left + 1];int k = 0;//记录新数组元素个数//数组1与数组2都有元素进行比较while (s1 <= mid && s2 <= right) {//因为是升序,谁小谁先进新数组tmpif(array[s1] < array[s2]) {tmp[k++] = array[s1++];}else {tmp[k++] = tmp[s2++];}}//如果比较的s1,s2数组不等长(两数组中元素个数不一致)//再次遍历剩余数组,将剩余元素放入新数组中while (s1 <= mid) {tmp[k++] = array[s1++];}while (s2 <= right) {tmp[k++] = array[s2++];}//新数组在放到旧数组中for (int i = 0; i < tmp.length; i++) {array[i + left] = array[i];}}

归并排序非递归实现:
思想: 分组排序,一组一个一个,在一组两个两个,再四个四个, 分完一组再归并;

代码实现:

 public void mergeSort2(int[] array) {//定义组数int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i += gap*2) {//i += gap*2 => 排完一组排一组,使最左下标更换以至于遍历全部数组元素int left = i;int mid = left + gap - 1;//中间下标越界if(mid > array.length) {mid = array.length - 1;}//右下标越界int right = mid + gap;if(right > array.length) {right = array.length - 1;}//排序merge(array,left,right,mid);}//增加每组的个数1->2,2->4等等gap *= 2;}}