本篇会解决一下几个问题：
1.堆是什么？
2.如何形成一个堆？
3.堆的应用场景
 

堆是什么？

• 堆总是一颗完全二叉树
• 堆的某个节点总是不大于或不小于父亲节点

如图，在小堆中，父亲节点总是小于孩子节点的。

 

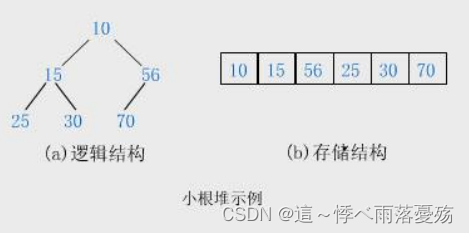
如图，在大堆中，父亲节点总是大于孩子节点的。

堆和二叉树还是有很大区别的，堆是用数组来实现的，尽管逻辑结构上是一颗二叉树，但在内存上要比二叉树好，普通的二叉树，你要用链表来存储他们的左右孩子，还要给他们分配空间，但堆只是用数组来表示。

如何形成一个堆？

堆的创建有向上调整和向下调整两种方式。

向上调整：从第一个非叶子节点开始向上调整，一直调整到根节点。

用int a[] ={1,5,3,8,7,6};来做例子，

如图所示，

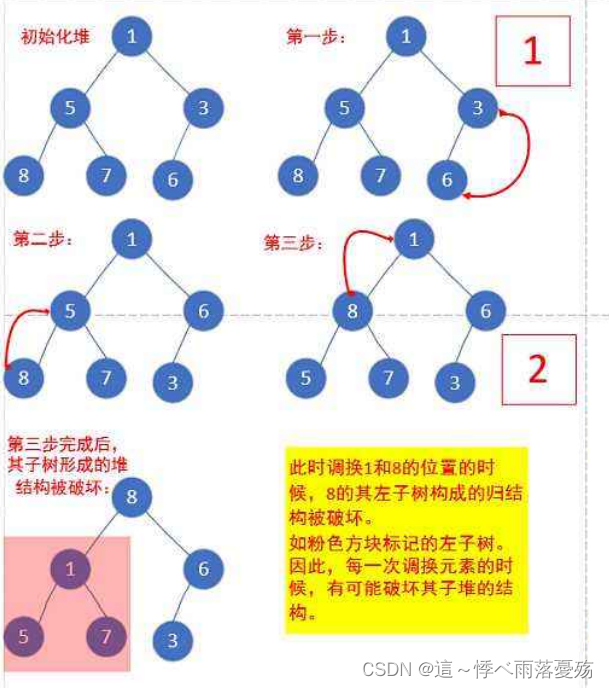
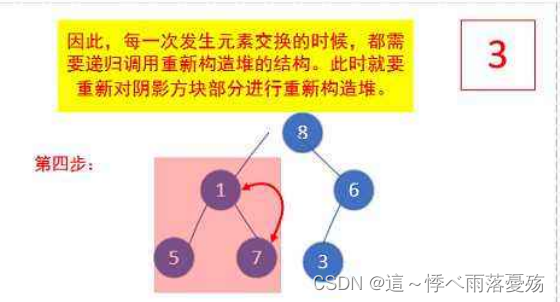
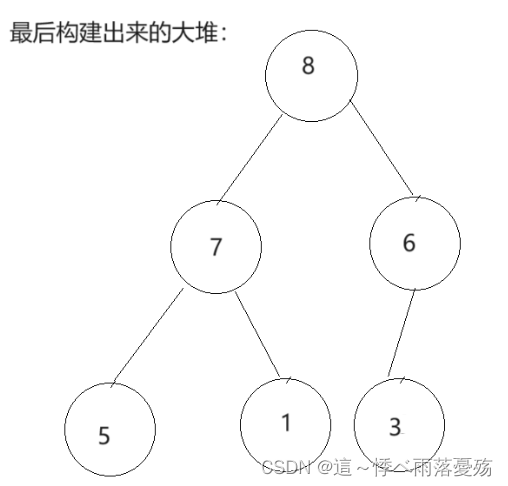
向下调整：从根节点开始，和左右孩子中小或者大的节点比较，交换，直到小于数组元素。

堆的插入

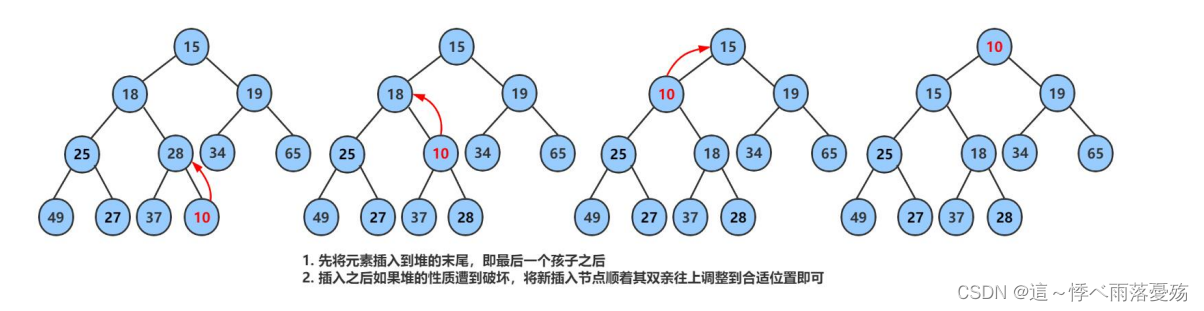
堆的删除

删除堆是删除堆顶的元素，将堆顶的元素根据最后一个数据一换，然后删除数组中最后一个元素，再进行向下调整算法。

这里想一想为什么要这样？？？

1.因为堆是有数组来创建的，如果直接删除堆顶的数据，第一个缺点就是会造成移动，从后往前覆盖，这样就会造成一个问题。兄弟节点变成父子节点，而且这样也不能很好的利用数组的优点。

2.如果是交换第一个和最后一个元素，这样有2个优点：

• 第一个是不会破坏除了堆顶的左右堆的结构。
• 第二个就是会利用数组的优点，数组读取速度很快，这样每次最后或最小的元素就放在了后面。
• 

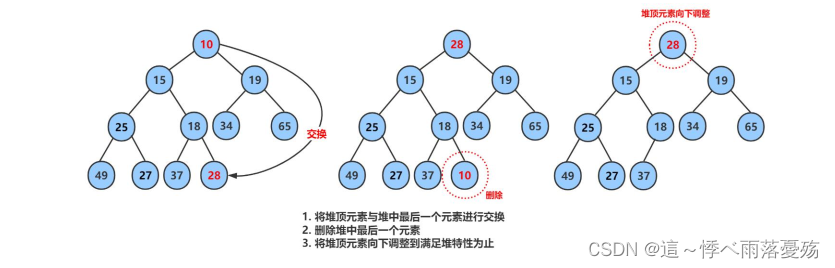
堆的时间复杂度

向下调整时间复杂度：

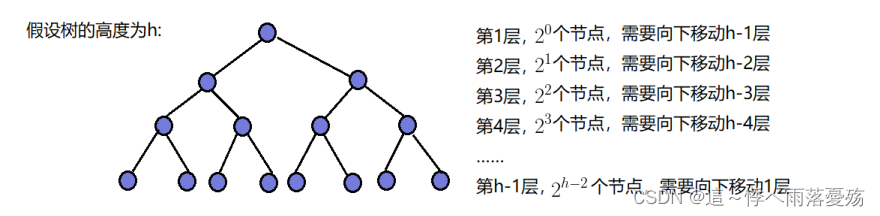 则要移动节点的总步数为：

向上调整时间复杂度：

则要调整的节点总数为：

堆的应用场景

1. 堆排序，可以用堆的建立和堆的删除来实现排序，堆排序十分稳定（相同元素的相对位置不会发生交换），而且时间复杂度都是O（N*logN）
2. TOP-K问题，我们想一想王者荣耀中前100的玩家是怎么实现的，或者专业前10名...问题

1）.先回答一下TOP-K问题：即求数据结合中前K个最大的元素或最小的元素，一把情况下数据很大。

2）.对于这种场景，首先想到的就是排序，但是：数据非常大，排序就不可取了，因为内存大小的原因，不会全部加载到内存，这时堆就发生了巨大的优势。

思路：利用K个元素建堆，如果是求最大的K个元素，就建立小堆，求最小的K歌元素，就建立大堆。然后用N-K个元素与堆顶元素比较，满足条件就交换。

下面是源码：

void HeapInit(Heap* php)
{assert(php);php->a = NULL;php->size = php->capacity =0;
}void HeapDestroy(Heap* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size =0;
}void Swap(HeapDateType* child, HeapDateType* parent){HeapDateType tmp = *child;*child=  *parent;*parent = tmp;
}void AdjustUp(HeapDateType* a,int child){int parent = (child-1)/2;while(child > 0){if(a[child] < a[parent]){Swap(&a[child],&a[parent]);child = parent;parent = (child-1)/2;}else{break;}
}}void HeapPush(Heap* php,HeapDateType x)
{assert(php);if(php->size == php->capacity){int newCapacity = php->capacity == 0?4:php->capacity*2;HeapDateType* tmp = (HeapDateType*)realloc(php->a,sizeof(HeapDateType)*newCapacity);if(tmp == NULL){perror("realloc fail\n");}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a,php->size-1);
}void HeapPrint(Heap* php)
{assert(php);for(size_t i =0; i<php->size; i++){std::cout << php->a[i] << " ";}std::cout << std::endl;
}void AdjustDown(HeapDateType* a,int n, int parent)
{int child = parent*2+1;while(child < n){if(child+1 < n && a[child+1] < a[child]){child++;}if(a[child] < a[parent]){Swap(&a[child],&a[parent]);parent = child;child = parent*2+1;}else{break;}}
}HeapDateType HeapTop(Heap* php)
{assert(php);assert(php->size > 0);return php->a[0];
}void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0],&php->a[php->size-1]);--php->size;AdjustDown(php->a,php->size,0);}bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}

 

void HeapSort(int* a, int n)
{//向上调整 O(n*logn)
//  for(size_t i =1; i<n; i++){
//    AdjustUp(a,i);
//  }
////向下调整 O(n)for(int i = (n-2)/2; i>=0; i--){AdjustDown(a,n,i);}//时间复杂度O(N*logN)int end = n-1;while(end > 0){Swap(&a[0],&a[end]);AdjustDown(a,end,0);--end;}
}void PrintTopK(const char* filename,int k)
{FILE* fout = fopen(filename,"r");if(fout == NULL){perror("fopen fail");exit(-1);}int* minHeap = (int*)malloc(sizeof(int)*k);if(minHeap == NULL){perror("malloc fail");exit(-1);}for(int i =0; i<k; i++){fscanf(fout,"%d",&minHeap[i]);}for(int i = (k-2)/2; i>=0; i++){AdjustDown(minHeap,k,0);}int x =0;while(fscanf(fout,"%d",&x)!= EOF){if(x > minHeap[0]){minHeap[0] = x;AdjustDown(minHeap,k,0);}}for(int i =0; i<k; i++){std::cout << minHeap[i] << " ";}std::cout << std::endl;
}