汉诺塔专题：P1760 通天之汉诺塔题解 + Problem D: 汉诺塔题解

1. P1760 通天之汉诺塔题解

题目背景

直达通天路·小A历险记第四篇

题目描述

在你的帮助下，小 A 成功收集到了宝贵的数据，他终于来到了传说中连接通天路的通天山。但是这距离通天路仍然有一段距离，但是小 A 突然发现他没有地图！！！但是幸运的是，他在山脚下发现了一个宝箱。根据经验判断（小 A 有经验吗？），地图应该就在其中！

在宝箱上，有三根柱子以及在一根柱子上的 n 个圆盘。小 A 在经过很长时间判断后，觉得这就是 hanoi 塔！（这都要琢磨）。但是移动是需要时间的，所以小 A 必须要通过制造延寿药水来完成这项任务。现在，他请你告诉他需要多少步完成，以便他造足够的延寿药水。

输入格式

一个数 n，表示有 n 个圆盘。

输出格式

一个数 s，表示需要 s 步。

输入输出样例

输入 #1

输出 #1

2147483647

输入 #2

输出 #2

说明/提示

数据范围及约定

对于所有数据，n≤15000。

代码：

#include <iostream>
#include <vector>using namespace std;int main() {int n;cin >> n;vector<int> digits;digits.push_back(1); // 初始为1，逆序存储for (int i = 0; i < n; ++i) {int carry = 0;for (int j = 0; j < digits.size(); ++j) {int temp = digits[j] * 2 + carry;digits[j] = temp % 10;carry = temp / 10;}if (carry != 0) {digits.push_back(carry);}}// 减一操作int borrow = 1;for (int i = 0; i < digits.size() && borrow != 0; ++i) {digits[i] -= borrow;if (digits[i] < 0) {digits[i] += 10;borrow = 1;} else {borrow = 0;}}// 去除前导零while (!digits.empty() && digits.back() == 0) {digits.pop_back();}if (digits.empty()) {cout << 0;} else {for (auto it = digits.rbegin(); it != digits.rend(); ++it) {cout << *it;}}cout << endl;return 0;
}

代码解释：

代码逻辑分析

1. 输入处理

读取整数 n，表示需要计算的次方数。

2. 初始化大数存储

使用动态数组 digits 逆序存储大数，初始值为 [1]（即 20=1）。
逆序存储意味着低位在前，高位在后。例如，数值 123 存储为 [3, 2, 1]。

3. 计算 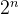$2^n$

通过 n 次循环，每次将当前数值乘以 2。
处理进位：
- 遍历每一位数字，计算 当前位 × 2 + 进位。
- 更新当前位为结果的个位，进位为十位。
- 若所有位处理完仍有进位，将其作为新高位加入数组。

示例：初始为 1，计算 23=8：

第1次循环：1×2 → 2 → [2]
第2次循环：2×2 → 4 → [4]
第3次循环：4×2 → 8 → [8]

4. 减一操作

从最低位开始借位减一：
- 若当前位减一后为负数，加 10 并设置借位。
- 否则，直接减一并结束借位。

示例： $2^4$ =16 减一：

数值 16 存储为 [6, 1]。
减一后，低位 6 → 5，无借位，结果为 [5, 1]（即 15）。

5. 去除前导零

逆序存储中前导零位于数组末尾，需移除。
若所有位均为零，最终输出 0。

6. 输出结果

逆序输出数组，得到正确的高位到低位顺序。

代码示例解析（以 n=3 为例）

计算 $2^3$ =8：
- 初始 digits = [1]。
- 3次循环后，digits = [8]（逆序存储 8）。
减一：
- 8 - 1 = 7 → digits = [7]。
输出：
- 逆序输出 7。

2. Problem D: 汉诺塔题解

Description

有三根柱A，B，C在柱A上有N块盘片，所有盘片都是大的在下面，小片能放在大片上面。现要将A上的N块片移到C柱上，每次只能移动一片，而且在同一根柱子上必须保持上面的盘片比下面的盘片小，请输出移动的步骤。

Input

输入整数n，表示有n块盘片

Output

输出移动的步骤

Sample Input

Sample Output

1 A->C
2 A->B
3 C->B
4 A->C
5 B->A
6 B->C
7 A->C

HINT

0 < n < 20

代码：

#include <cstdio>
#include <vector>
#include <string>
#include <cstring>using namespace std;vector<string> steps;
int step = 0;void hanoi(int n, char from, char to, char via) {if (n == 1) {step++;char buffer[20];snprintf(buffer, sizeof(buffer), "%d %c->%c", step, from, to);steps.emplace_back(buffer);} else {hanoi(n - 1, from, via, to);step++;char buffer[20];snprintf(buffer, sizeof(buffer), "%d %c->%c", step, from, to);steps.emplace_back(buffer);hanoi(n - 1, via, to, from);}
}int main() {int n;scanf("%d", &n);steps.reserve((1 << n) - 1); // 预分配足够内存hanoi(n, 'A', 'C', 'B');// 计算总输出长度size_t total_len = 0;for (const auto& s : steps) {total_len += s.size() + 1; // 每行加换行符}// 合并到缓冲区并一次性输出char* buffer = new char[total_len];char* ptr = buffer;for (const auto& s : steps) {size_t len = s.size();memcpy(ptr, s.c_str(), len);ptr += len;*ptr++ = '\n';}fwrite(buffer, 1, total_len, stdout);delete[] buffer;return 0;
}

代码解释：

汉诺塔独特递归算法：
- hanoi 函数递归地将 n 个盘子从起始柱 from 移动到目标柱 to，借助中间柱 via。
- 当 n=1 时，直接将盘子从 from 移到 to，记录步骤。
- 对于 n>1，分解为三步：
  - 将 n-1 个盘子从 from 移至 via（递归调用）。
  - 将第 n 个盘子从 from 移至 to。
  - 将 n-1 个盘子从 via 移至 to（递归调用）。
记录步骤：
- 使用全局变量 steps（vector<string>）存储每一步操作。
- 每移动一个盘子，递增全局变量 step，并用 snprintf 格式化为字符串（如 "1 A->C"）存入 steps。
性能优化：
- 内存预分配：steps.reserve((1 << n) - 1) 预分配足够内存，避免 vector 动态扩容的开销。
- 单次输出：计算所有步骤字符串的总长度，合并到连续内存缓冲区，通过 fwrite 一次性输出，减少频繁I/O操作的开销。
代码结构：
- 全局变量：steps 和 step 简化参数传递，但在多线程环境中不安全（此处单线程无问题）。
- 递归实现：清晰体现汉诺塔问题分治思想，时间复杂度为 O(2ⁿ)。
- 输入输出：scanf 读取盘子数 n，高效输出避免逐行打印。