目录
- 一、平衡二叉树的定义
- 二、平衡因子
- 三、平衡二叉树的插入和构造
- (一)LL型旋转
- (二)LR型旋转
- (三)RR型旋转
- (四)RL型旋转
- 四、平衡二叉树的删除
- (一)叶子结点
- (二)只有左/右子树,没有右/左子树
- (三)既有左子树,又有右子树
- 五、平衡二叉树的查找和平均查找长度
一、平衡二叉树的定义
平衡二叉树以二叉排序树为基础,若二叉排序树中左、右子树的高度之差的绝对值不超过1,则称为平衡二叉树(AVL树),其左、右子树也为一棵平衡二叉树,其平均查找长度为O(log2n),如下:
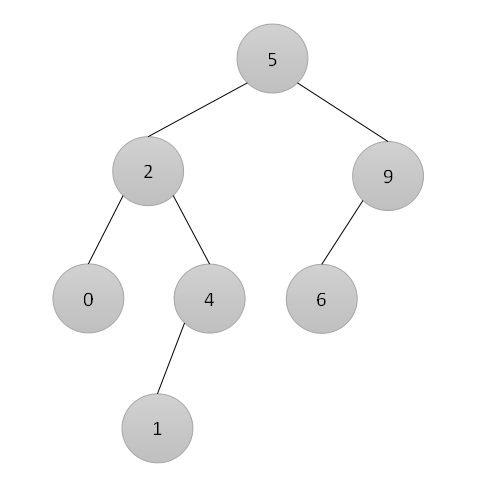
二、平衡因子
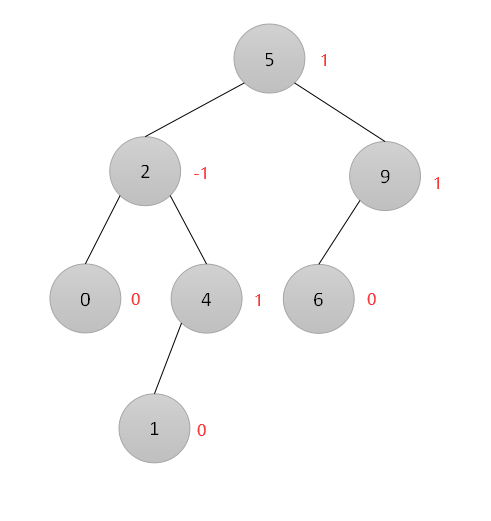
二叉树中左子树的深度减去其右子树深度,称为该结点的平衡因子,平衡二叉树中结点的平衡因子只可能为1、-1或0三种,其中叶子结点的平衡因子均为0,例如下面这个二叉树为平衡二叉树:
叶子结点0、1、6的平衡因子均为0,
结点4的左子树深度为1,右子树深度为0,所以平衡因子为1-0=1,
结点9的左子树深度为1,右子树深度为0,所以平衡因子为1-0=1,
结点2的左子树深度为1,右子树深度为2,所以平衡因子为1-2=-1,
结点5的左子树深度为3,右子树深度为2,所以平衡因子为3-2=1。
而,下图这个二叉树为非平衡二叉树:
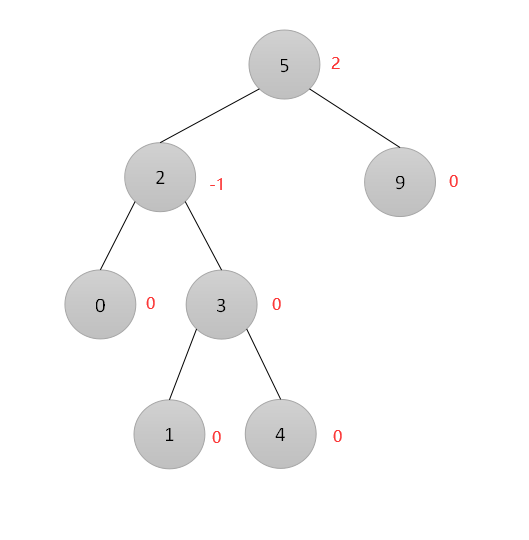
叶子结点0、1、4、9的平衡因子均为0,
结点3的左子树深度为1,右子树深度为1,所以平衡因子为1-1=0,
结点2的左子树深度为1,右子树深度为2,所以平衡因子为1-2=-1,
结点5的左子树深度为3,右子树深度为1,所以平衡因子为3-1=2,不满足平衡二叉树的要求。
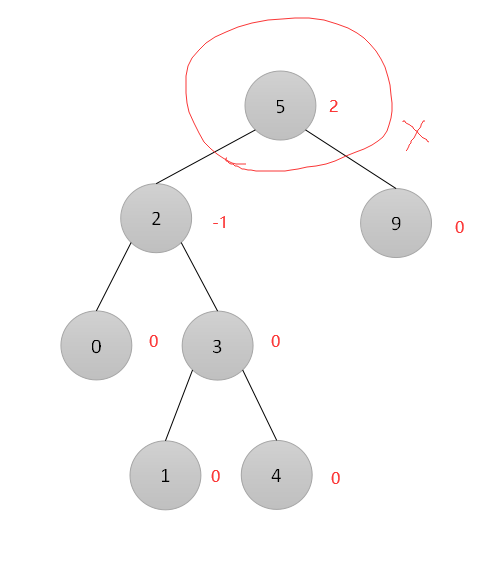
三、平衡二叉树的插入和构造
平衡二叉树的插入操作性质与二叉排序树一样,也是要在保证一定条件下进行插入操作,若导致不满足条件则需要进行调整。若平衡二叉树中插入一个元素时导致发生了不平衡,则需要调整元素的位置关系,使其达到平衡。
插入新结点导致不平衡的情况有以下四种:
| 类别 | 操作 |
|---|---|
| LL型旋转(右单旋转) | 在结点的左子树的左子树插入新结点导致失衡 |
| LR型旋转(先左后右旋转) | 在结点的左子树的右子树插入新结点导致失衡 |
| RR型旋转(左单旋转) | 在结点的右子树的右子树插入新结点导致失衡 |
| RL型旋转(先右后左旋转) | 在结点的右子树的左子树插入新结点导致失衡 |
(一)LL型旋转
若在结点的左子树的左子树插入新结点导致平衡二叉树失衡,则进行LL型旋转,即右单旋转。

插入新结点6后导致平衡二叉树失衡,插入位置是结点9的左子树的左子树处,所以进行LL型旋转,如下:
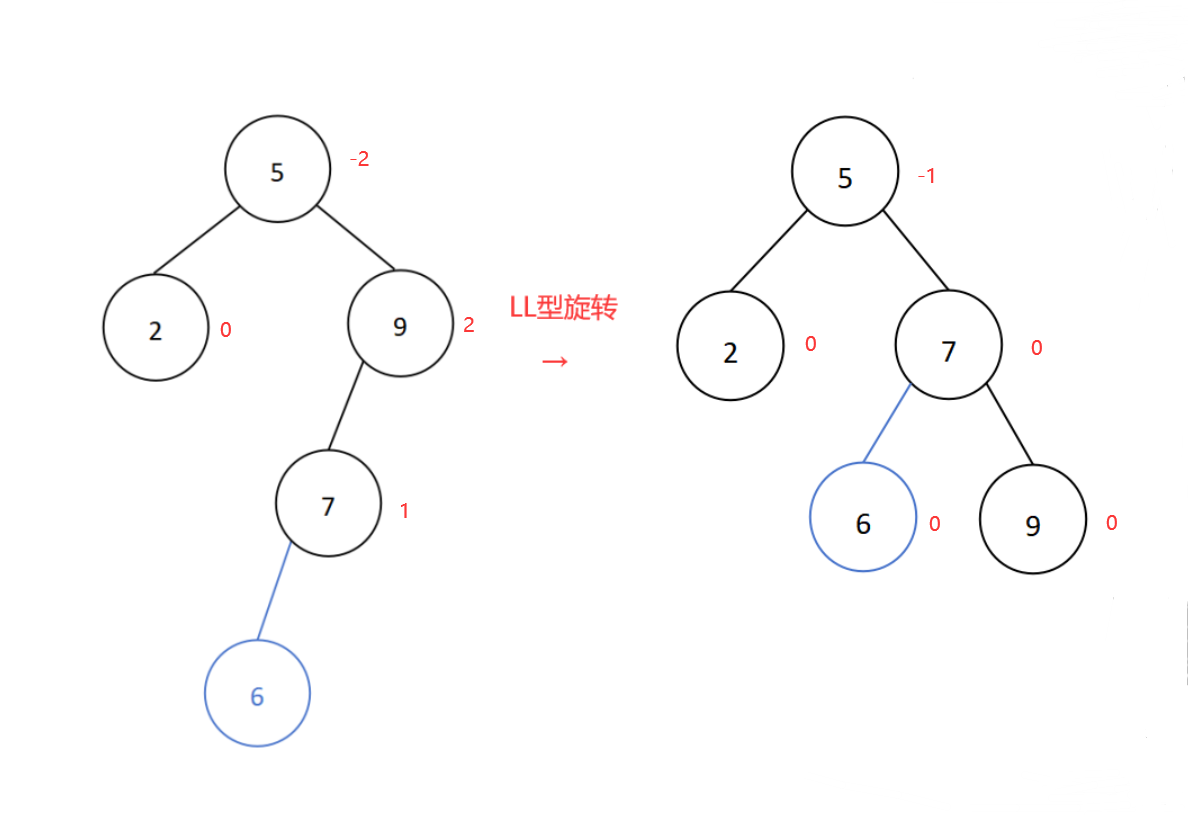
调整后的二叉树即为平衡二叉树。
(二)LR型旋转
若在结点的左子树的右子树插入新结点导致平衡二叉树失衡,则进行LR型旋转,即先左后右旋转。
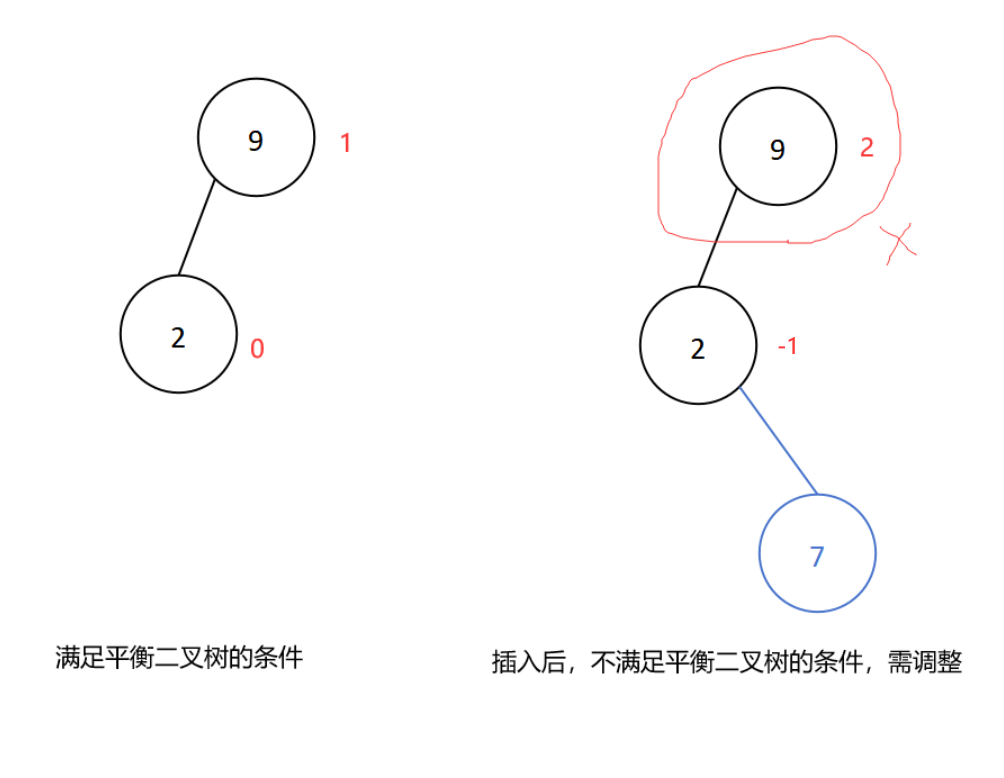
插入新结点7后导致平衡二叉树失衡,插入位置是结点9的左子树的右子树处,所以进行LR型旋转,如下:
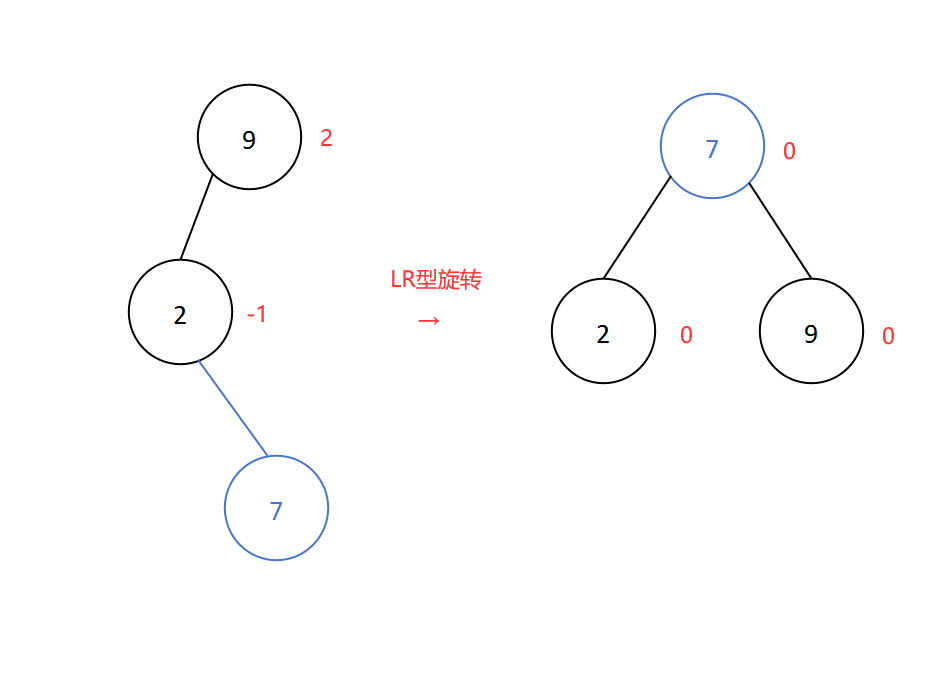
调整后的二叉树即为平衡二叉树。
(三)RR型旋转
若在结点的右子树的右子树插入新结点导致平衡二叉树失衡,则进行RR型旋转,即左单旋转。
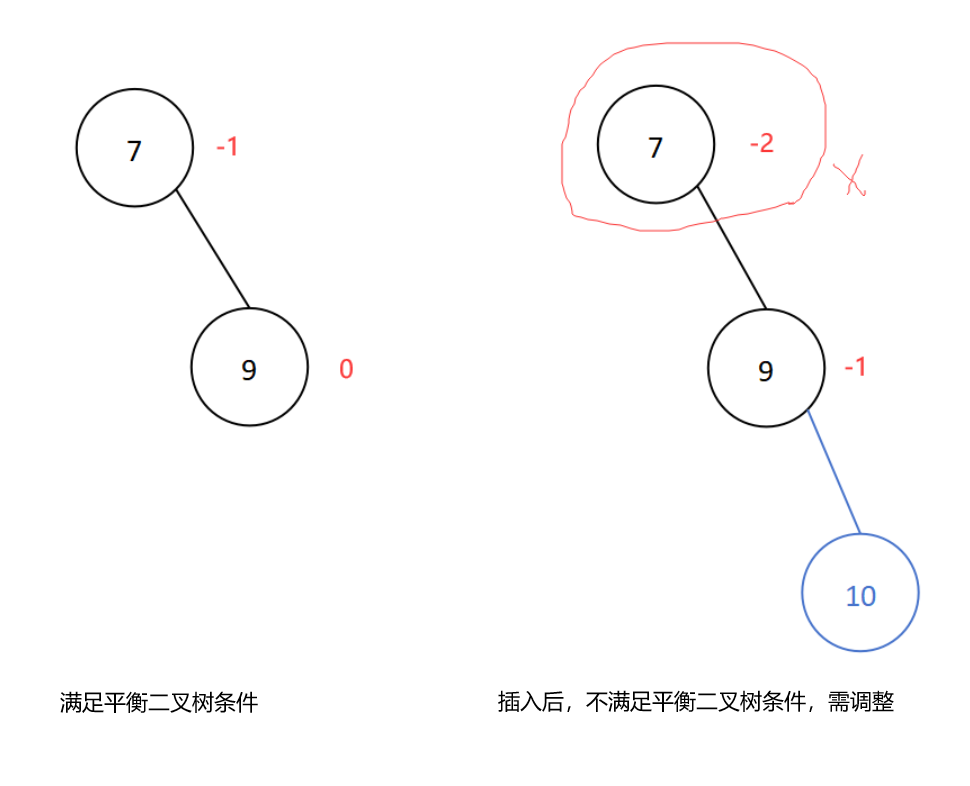
插入新结点10后导致平衡二叉树失衡,插入位置是结点7的右子树的右子树处,所以进行RR型旋转,如下:
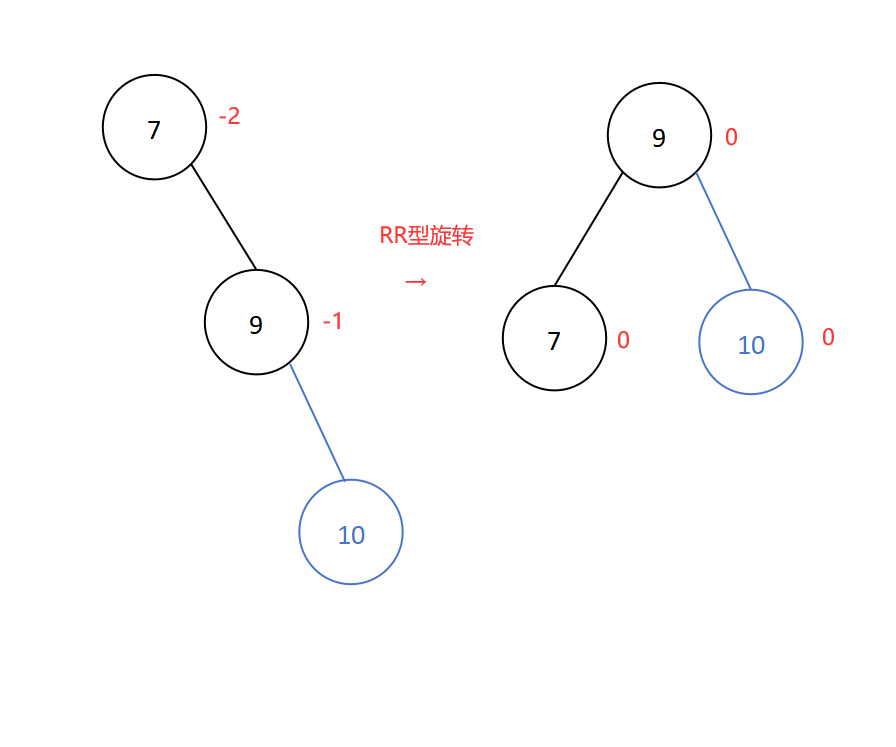
调整后的二叉树即为平衡二叉树。
(四)RL型旋转
若在结点的右子树的左子树插入新结点导致平衡二叉树失衡,则进行RL型旋转,即先右后左旋转。
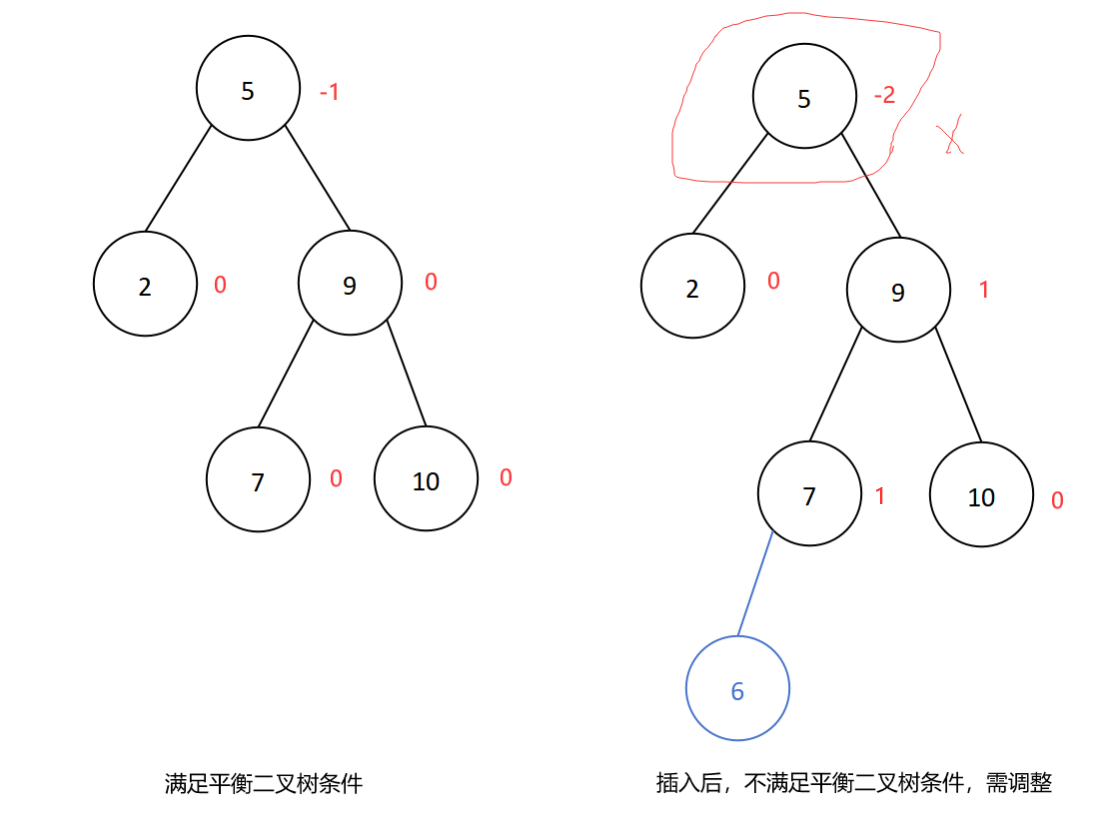
插入新结点6后导致平衡二叉树失衡,插入位置是结点5的右子树的左子树处,所以进行RL型旋转,如下:
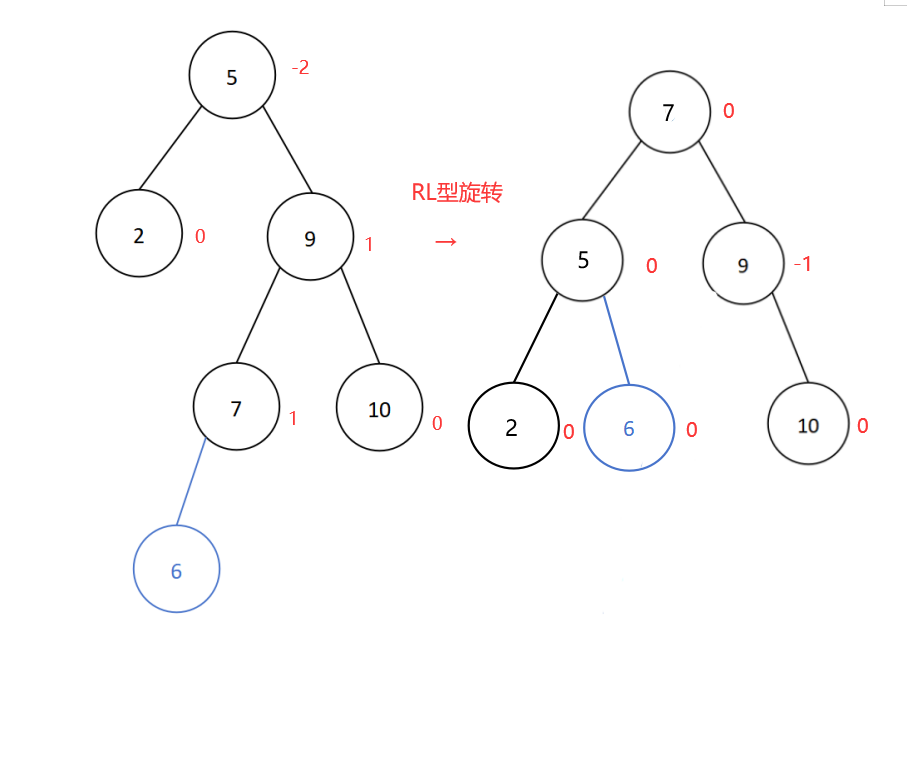
调整后的二叉树即为平衡二叉树。
四、平衡二叉树的删除
(一)叶子结点
平衡二叉树中,若要删除的结点只有叶子结点,则可直接将其删除,不影响平衡二叉树。
例如,删除平衡二叉树中的结点9,由于该结点是叶子结点,所以直接删除,如下:

(二)只有左/右子树,没有右/左子树
平衡二叉树中,若要删除的结点只有左/右子树,没有右/左子树,此时将该结点删除,后面的子结点接上即可,从而不影响平衡二叉树。
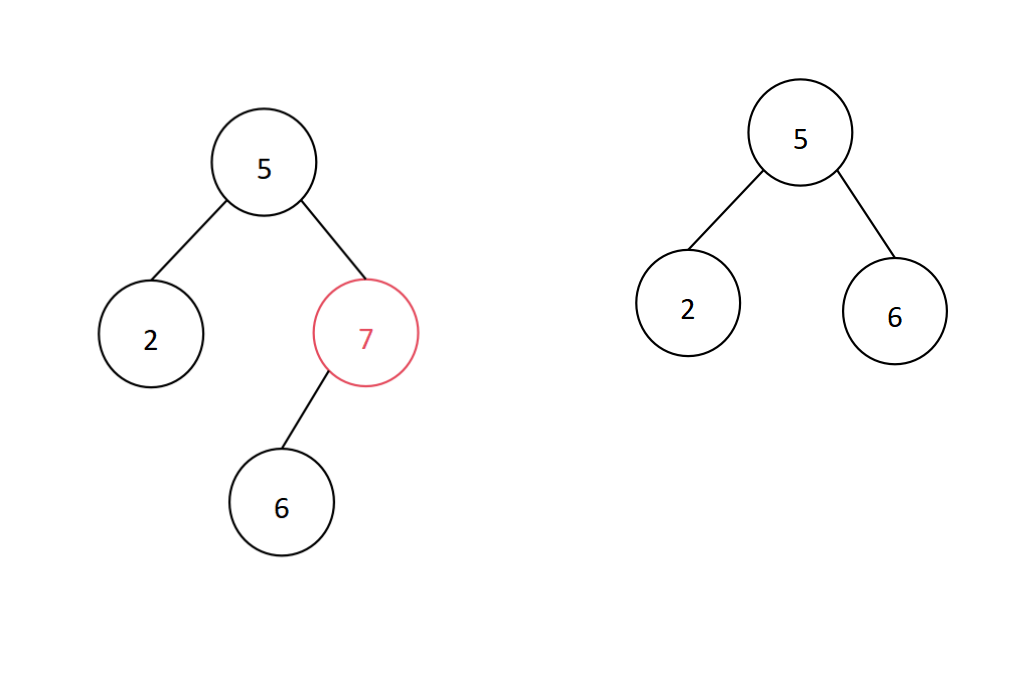
(三)既有左子树,又有右子树
平衡二叉树中,若要删除的结点既有左子树,又有右子树,此时可沿着左(右)子树的右(左)指针,一直走到右(左)子树的最右(左)边的一个结点,用该结点与要删除的结点代替【找到交换的结点】,然后,可以将其转换为(一)、(二)中的情况,若替代后,该结点为叶子结点则按照(一)进行删除,若非叶子结点则按照(二)进行删除。
例如,删除平衡二叉树中结点11,首先找到要交换的结点,即结点9,所以结点11与结点9进行交换,如下:
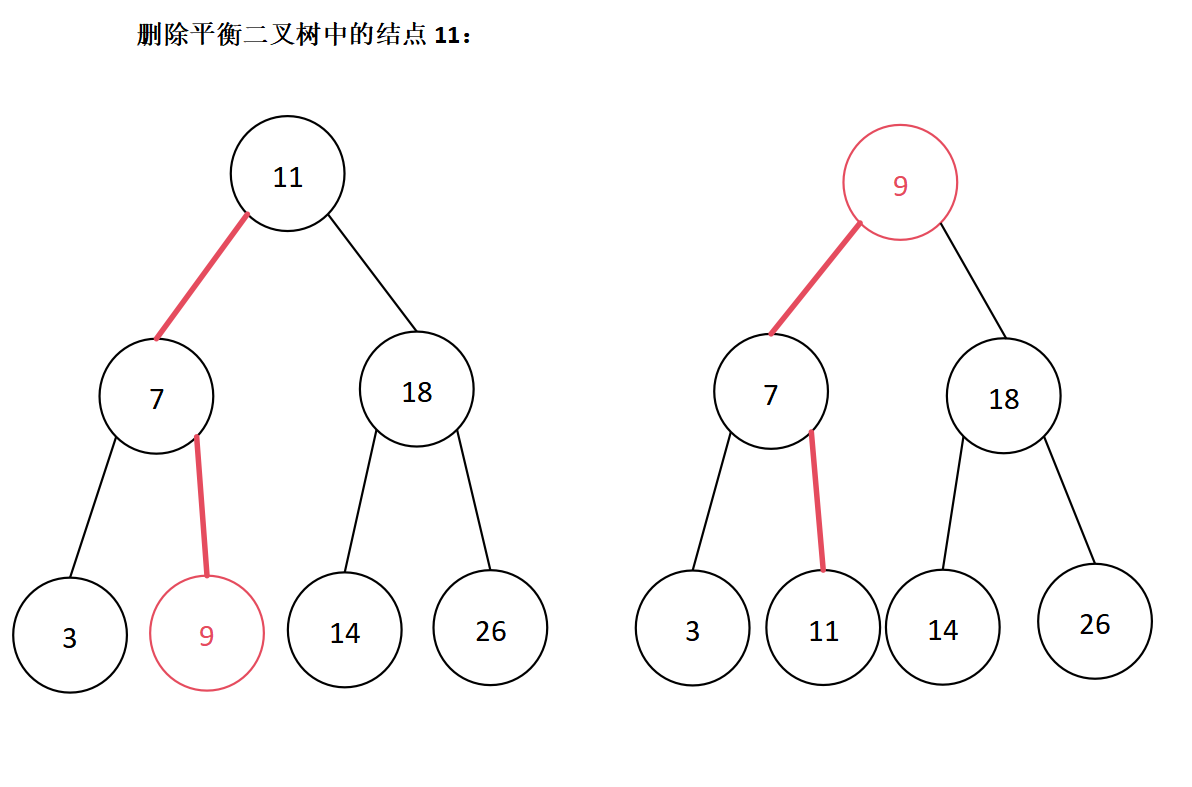
然后,由于此时结点11是叶子结点,此时转换为第一种情况,所以可直接删除,如下:
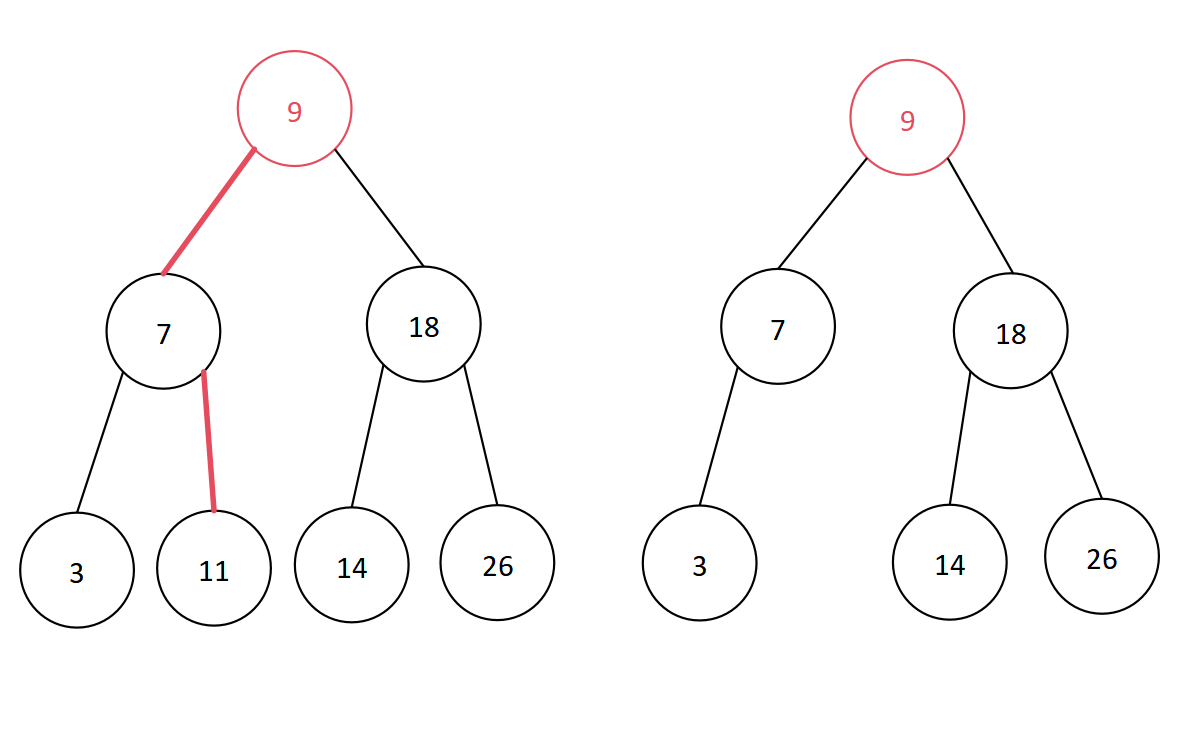
五、平衡二叉树的查找和平均查找长度
平衡二叉树的查找与二叉排序树一样,含有n个结点的平衡二叉树的最大深度为h=⌈log2(n+1)⌉,所以其平均查找长度为O(log2n),另外平衡二叉树的最小深度为h=⌈log2(n+1)⌉。










)








