【代码随想录——单调栈】

1.每日温度

在这里插入图片描述

func dailyTemperatures(temperatures []int) []int {stack := list.New()//入栈：stack.PushBack()//出栈：stack.Remove(stack.Back())dp := make([]int, len(temperatures))for i := 0; i < len(temperatures); i++ {if stack.Len() == 0 {stack.PushBack(i)} else {if temperatures[stack.Back().Value.(int)] >= temperatures[i] {stack.PushBack(i)} else {for stack.Len() != 0 && temperatures[stack.Back().Value.(int)] < temperatures[i] {// 设置dpdp[stack.Back().Value.(int)] = i - stack.Back().Value.(int)// 出栈stack.Remove(stack.Back())}stack.PushBack(i)}}}return dp
}

2.下一个更大元素I

在这里插入图片描述

func nextGreaterElement(nums1 []int, nums2 []int) []int {stack := list.New()//入栈：stack.PushBack()//出栈：stack.Remove(stack.Back())dp := make([]int, len(nums2))m := make(map[int]int,0)for i := 0; i < len(nums2); i++ {m[nums2[i]] = iif stack.Len() == 0 {stack.PushBack(i)} else {if nums2[stack.Back().Value.(int)] >= nums2[i] {stack.PushBack(i)} else {for stack.Len() != 0 && nums2[stack.Back().Value.(int)] < nums2[i] {// 设置dpdp[stack.Back().Value.(int)] = i - stack.Back().Value.(int)// 出栈stack.Remove(stack.Back())}stack.PushBack(i)}}}//计算结果ans := make([]int,len(nums1))for i:=0;i<len(nums1);i++{index := m[nums1[i]]hasMoreBigger := dp[index]if hasMoreBigger==0{ans[i]=-1}else{ans[i]=nums2[index+dp[index]]}}return ans
}

3.下一个更大元素II

在这里插入图片描述

func nextGreaterElements(nums []int) []int {stack := list.New()//入栈：stack.PushBack()//出栈：stack.Remove(stack.Back())dp := make([]int,len(nums))for i:=0;i<len(nums);i++{dp[i] = -1}m := make(map[int]int,0)for i:=0;i<len(nums)*2;i++{index := i%len(nums)m[nums[index]] = indexif stack.Len()==0 || nums[stack.Back().Value.(int)] >= nums[index]{stack.PushBack(index)}else{for stack.Len() != 0 && nums[stack.Back().Value.(int)] < nums[index] {// 设置dpdp[stack.Back().Value.(int)] = nums[index]// 出栈stack.Remove(stack.Back())}stack.PushBack(index)}}return dp
}

4. 接雨水

在这里插入图片描述

4.1 暴力解法

记录左边柱子的最高高度和右边柱子的最高高度，就可以计算当前位置的雨水面积

func trap(height []int) int {sum := 0for i:=0;i<len(height);i++{// 第一个柱子和最后一个柱子不接雨水if i==0||i==len(height)-1{continue}rHeight := height[i]//记录右边柱子的最高高度lHeight := height[i]//记录左边柱子的最高高度//向右查找最高高度for r:=i+1;r<len(height);r++{if height[r]>rHeight{rHeight = height[r]}}//向左查找最高高度for l:=i-1;l>=0;l--{if height[l]>lHeight{lHeight = height[l]}}h := min(lHeight,rHeight) - height[i]if h>0 {sum += h}}return sum
}

4.2 双指针优化

为了得到两边的最高高度，使用了双指针来遍历，每到一个柱子都向两边遍历一遍，这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上（maxLeft），右边最高高度记录在一个数组上（maxRight），这样就避免了重复计算。

func trap(height []int) int {sum := 0if len(height)<=2{return sum}maxLeft := make([]int,len(height))maxRight := make([]int,len(height))// 记录每个柱子左边柱子最大高度maxLeft[0] = height[0];for i := 1; i < len(height); i++ {maxLeft[i] = max(height[i], maxLeft[i - 1]);}// 记录每个柱子右边柱子最大高度maxRight[len(height)-1] = height[len(height)-1];for i := len(height)-2; i >=0; i-- {maxRight[i] = max(height[i], maxRight[i + 1]);}// 求和for i:=0; i<len(height);i++{count := min(maxLeft[i],maxRight[i])-height[i]if count > 0{sum += count}}return sum
}

4.3 单调栈

情况一：当前遍历的元素（柱子）高度小于栈顶元素的高度 height[i] < height[st.top()]
- if (height[i] < height[st.top()]) st.push(i);
情况二：当前遍历的元素（柱子）高度等于栈顶元素的高度 height[i] == height[st.top()]
- if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况 st.pop(); st.push(i);}
情况三：当前遍历的元素（柱子）高度大于栈顶元素的高度 height[i] > height[st.top()]
- 计算凹槽的体积

func trap(height []int) int {sum := 0if len(height)<=2{return sum}st := list.New()//入栈：stack.PushBack()//出栈：stack.Remove(stack.Back())st.PushBack(0)for i:=1;i<len(height);i++{if height[i] < height[st.Back().Value.(int)]{//情况1st.PushBack(i)}else if height[i] == height[st.Back().Value.(int)]{//情况2st.Remove(st.Back())st.PushBack(i)}else{//情况3for st.Len()!=0 && height[i]>height[st.Back().Value.(int)]{mid := st.Back().Value.(int)st.Remove(st.Back())if st.Len()!=0{//求高度h := min(height[st.Back().Value.(int)],height[i])-height[mid]//求中间宽度w := i-st.Back().Value.(int)-1sum += h * w}}st.PushBack(i)}}return sum
}

5. 柱状图中最大的矩阵

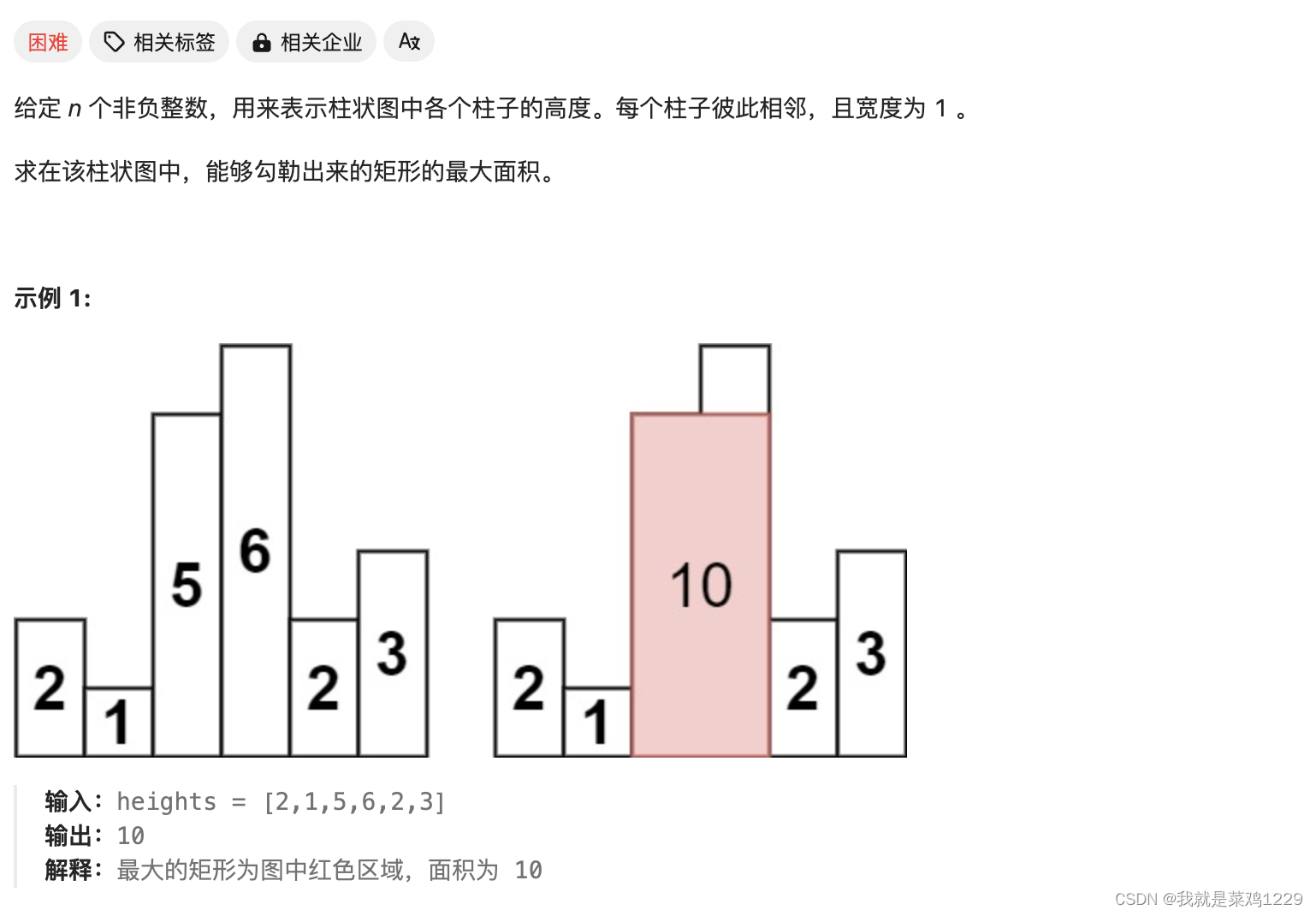
在这里插入图片描述

5.1 双指针法

这个方法比较通俗易懂。
记录每个柱子左右两边第一个小于该柱子的下标。
但是在leetcode上会超时，该测试用例的特点为所有的height都为一个值，会使得复杂度为n^2

func largestRectangleArea(heights []int) int {minLeftIndex := make([]int, len(heights))minRightIndex := make([]int, len(heights))// 寻找小于当前柱子的第一个柱子的IndexminLeftIndex[0] = -1for i := 1; i < len(heights); i++ {t := i - 1for t >= 0 && heights[t] >= heights[i] {t = t - 1}minLeftIndex[i] = t}minRightIndex[len(heights)-1] = len(heights)for i := len(heights) - 2; i >= 0; i-- {t := i + 1for t <= len(heights)-1 && heights[t] >= heights[i] {t = t + 1}minRightIndex[i] = t}result := 0for i := 0; i < len(heights); i++ {sum := heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1)result = max(sum, result)}return result
}

修改后的版本:

func largestRectangleArea(heights []int) int {minLeftIndex := make([]int, len(heights))minRightIndex := make([]int, len(heights))// 寻找小于当前柱子的第一个柱子的IndexminLeftIndex[0] = -1for i := 1; i < len(heights); i++ {t := i - 1for t >= 0 && heights[t] >= heights[i] {//在特殊情况下避免了大量的重复计算t = minLeftIndex[t]}minLeftIndex[i] = t}minRightIndex[len(heights)-1] = len(heights)for i := len(heights) - 2; i >= 0; i-- {t := i + 1for t <= len(heights)-1 && heights[t] >= heights[i] {//在特殊情况下避免了大量的重复计算t = minRightIndex[t];}minRightIndex[i] = t}result := 0for i := 0; i < len(heights); i++ {sum := heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1)result = max(sum, result)}return result
}

5.2 单调栈法

从栈头（元素从栈头弹出）到栈底的顺序应该是从大到小的顺序！

func largestRectangleArea(heights []int) int {max := 0// 使用切片实现栈stack := make([]int, 0)// 数组头部加入0heights = append([]int{0}, heights...)// 数组尾部加入0heights = append(heights, 0)// 初始化栈，序号从0开始stack = append(stack, 0)for i := 0; i < len(heights); i++ {// 结束循环条件为：当即将入栈元素>top元素，也就是形成非单调递增的趋势for heights[i] < heights[stack[len(stack)-1]] {// mid是topmid := stack[len(stack)-1]// 出栈stack = stack[0 : len(stack)-1]// left是top的下一位元素，i是将要入栈的元素left := stack[len(stack)-1]// 高度x宽度tmp := heights[mid] * (i - left - 1)if tmp > max {max = tmp}}stack = append(stack, i)}return max
}