数据结构-----【链表:刷题】

-------------------------------------------基础题参照leetcode----------------------------------------------------------------------------------------------------------

【2】两数相加

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {int sub1=0,sub2=0,count=0,temp =0;stack<int> temp_st;int sum=0;while(l1){temp_st.push(l1->val);l1 = l1->next;count++;//计数}while(count--){//while的逻辑，先使用count=3，然后再减小，再进来，count直接为2了sub1+= temp_st.top()*pow(10,count);temp_st.pop();}count =0;while(l2){temp_st.push(l2->val);l2 = l2->next;count++;//计数}while(count--){sub2+= temp_st.top()*pow(10,count);temp_st.pop();}sum = sub1+sub2;//头插法//ListNode* dummy = new  ListNode(0);ListNode* node = new ListNode(sum%10);//定义返回链表头ListNode* temp_node;sum /= 10;while(sum/10){temp_node = node;ListNode* node  = new ListNode(sum%10);node->next = temp_node;}return node;}
};

第二题的另外一种做法：

class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode *head = nullptr,*tail = nullptr;int carry=0;//两数都不会以0开头while(l1 ||l2){//除非链表都非空，否则继续执行int n1 = l1?l1->val:0;//l1非空指向l1->val，否则指向0int n2 = l2?l2->val:0;int sum = n1+n2+carry;//先加高位 7 ，再放到最后低位去，则carry为上次低位的进位值if (!head) {head = tail = new ListNode(sum % 10);} else {tail->next = new ListNode(sum % 10);tail = tail->next;}carry = sum / 10;//carry为进位值if (l1) {l1 = l1->next;}if (l2) {l2 = l2->next;}}if (carry > 0) {tail->next = new ListNode(carry);//尾插法，需要指定head在前面不动}return head;}
};

！！【148】排序链表

给你链表的头结点 head ，请将其按升序排列并返回 排序后的链表 。

方法一：转为数组

空间复杂度o(n),时间复杂度o(n)

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* sortList(ListNode* head) {int count =0;vector<int> temp_vec;ListNode* tail = nullptr;ListNode* head2 = nullptr;while(head){temp_vec.push_back(head->val);head= head->next;count++;}sort(temp_vec.begin(),temp_vec.end());tail = head2 = new ListNode(0);//尾插法for(int i =0;i<count;i++){tail->next = new ListNode(temp_vec[i]); tail = tail->next;}return head2->next;}
};

方法二：归并排序（分治算法）

自底向上归并排序，空间复杂度o(1).

首先先回顾一下递归调用：【21】合并两个有序链表

要明白，①递归函数必须要有终止条件。②递归函数先不断调用自身，直到遇到终止条件以后进行回溯，最终返回答案。

所以根据【21】题，终止条件：

两个链表为空，表示我们对链表已经合并完成。

如何递归：判断l1和l2哪个头结点更小，然后较小的结点的next指针指向其余结点的合并结果。(递归调用)

下面这个动画可以很形象地看出，先是调用自身，遇到终止条件以后，再进行回溯，返回答案的过程：

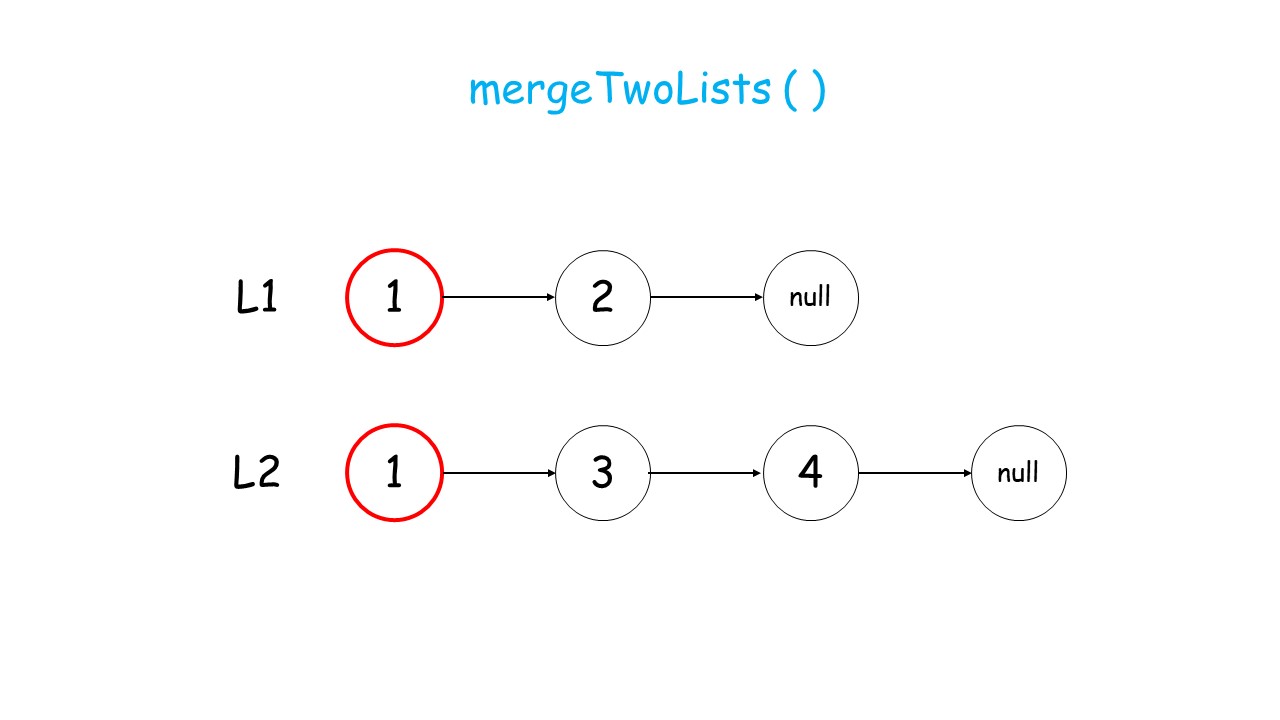
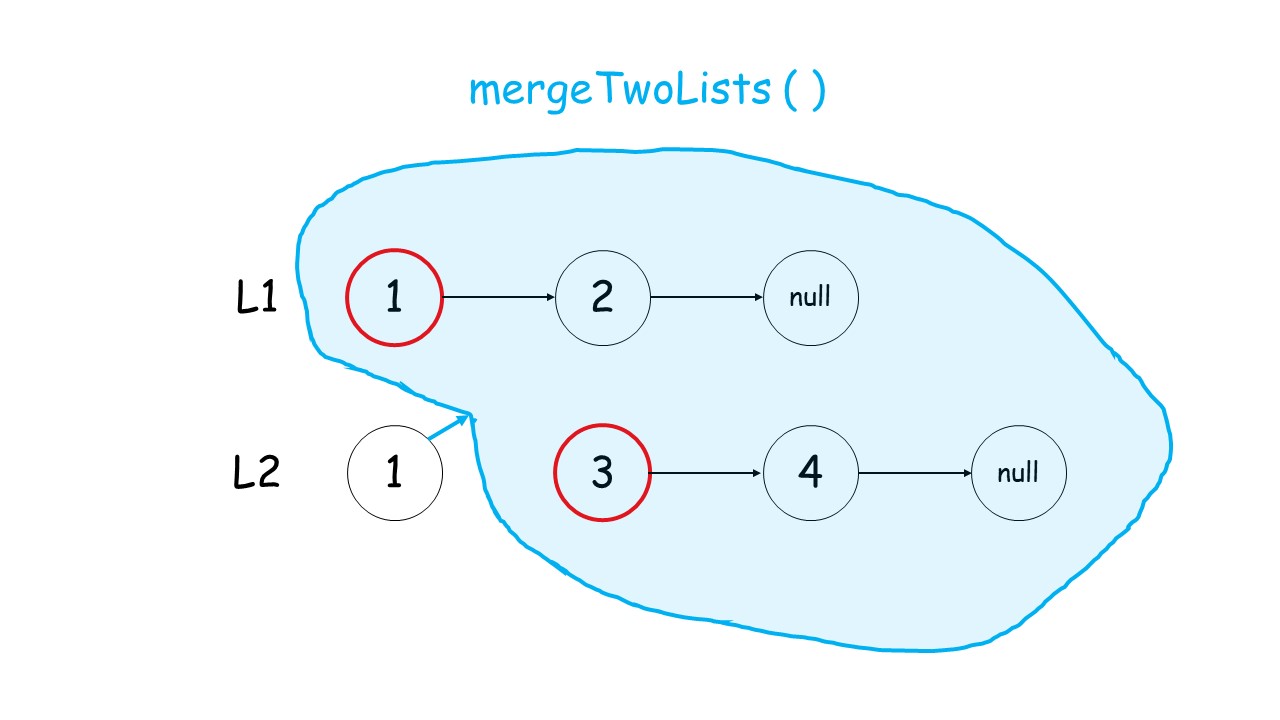
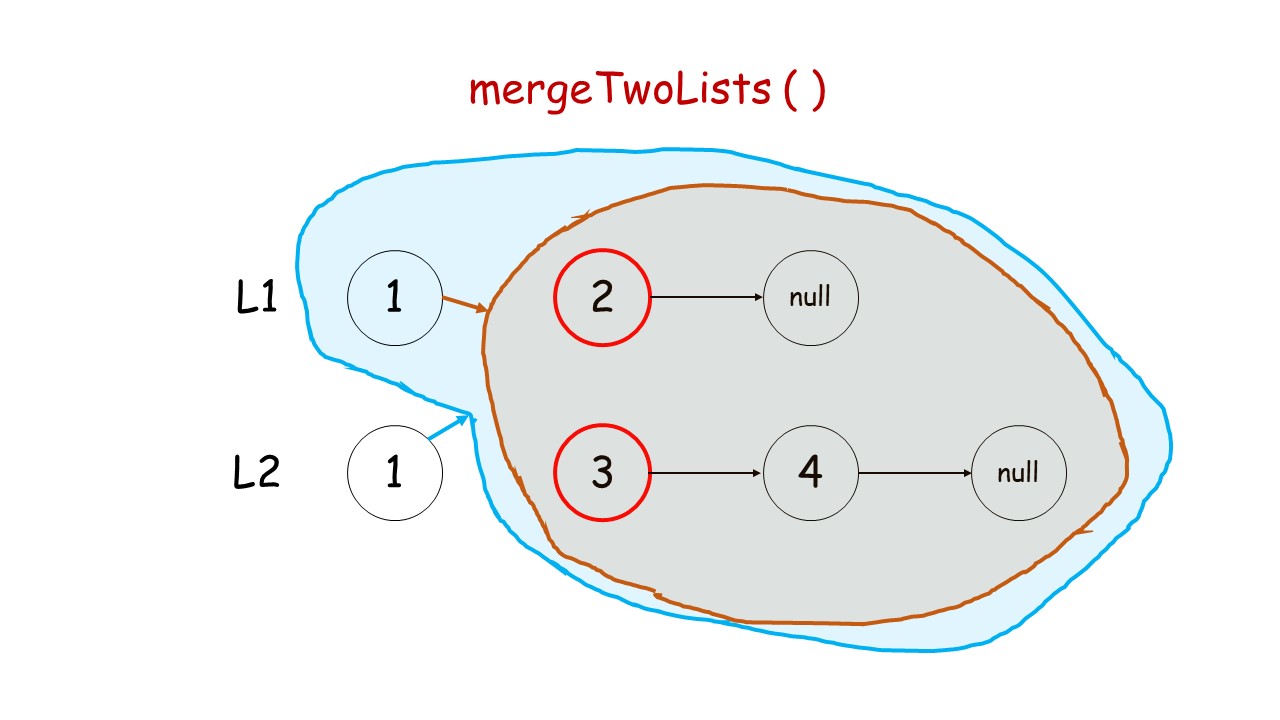
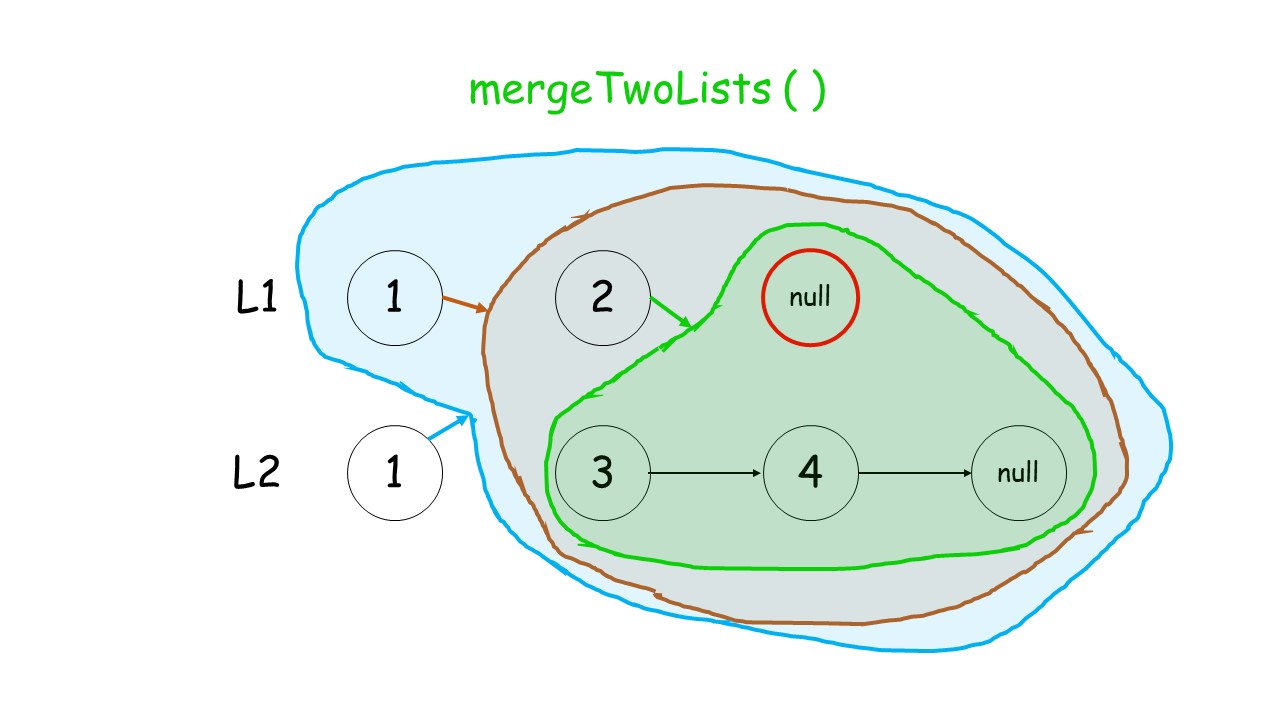
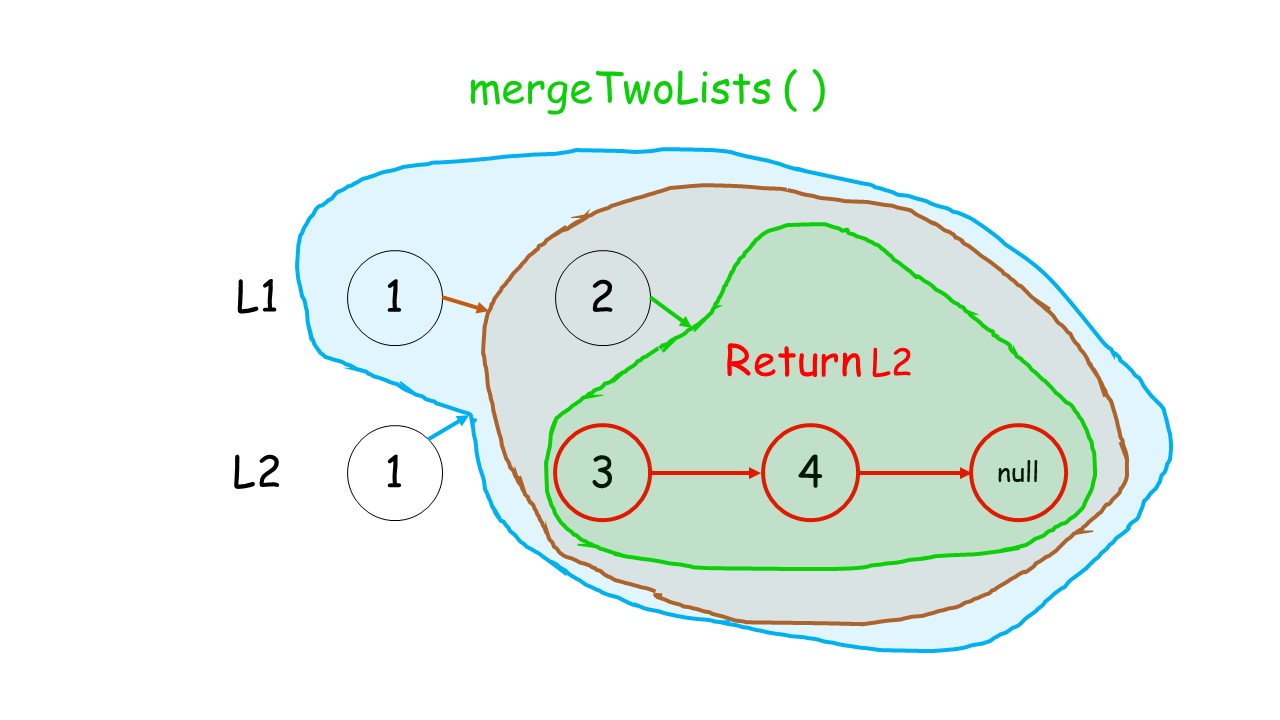
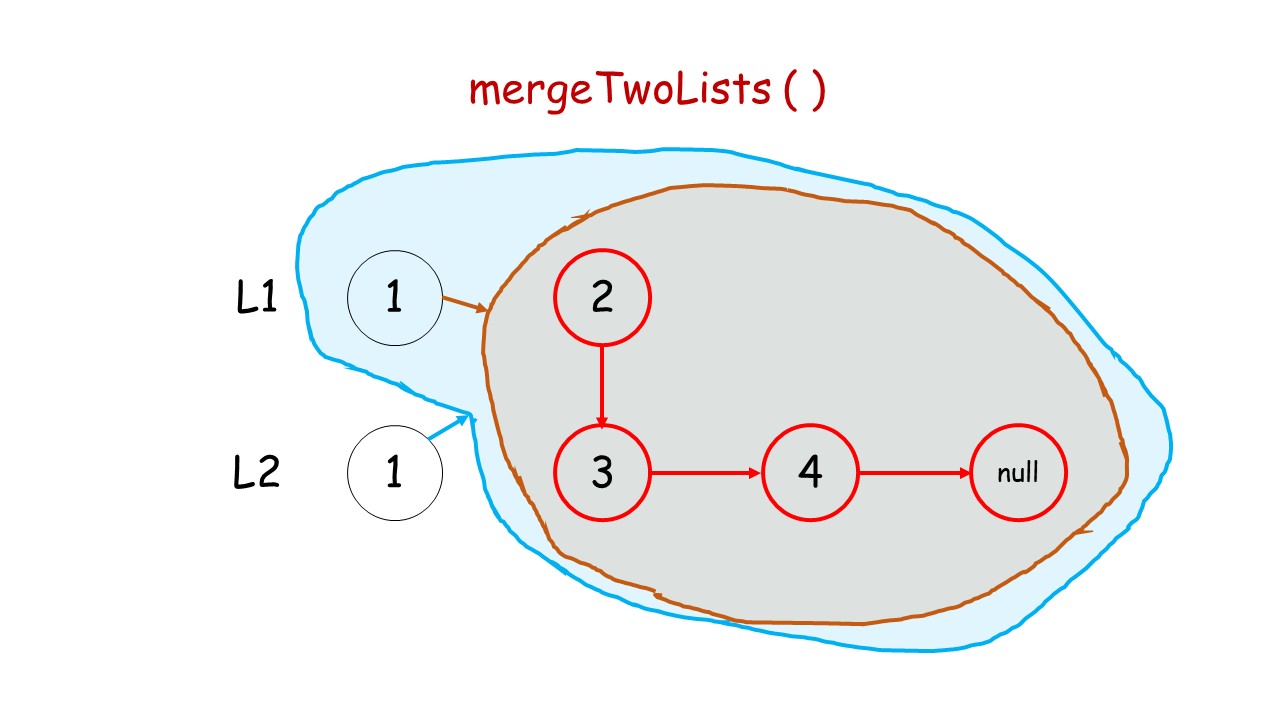
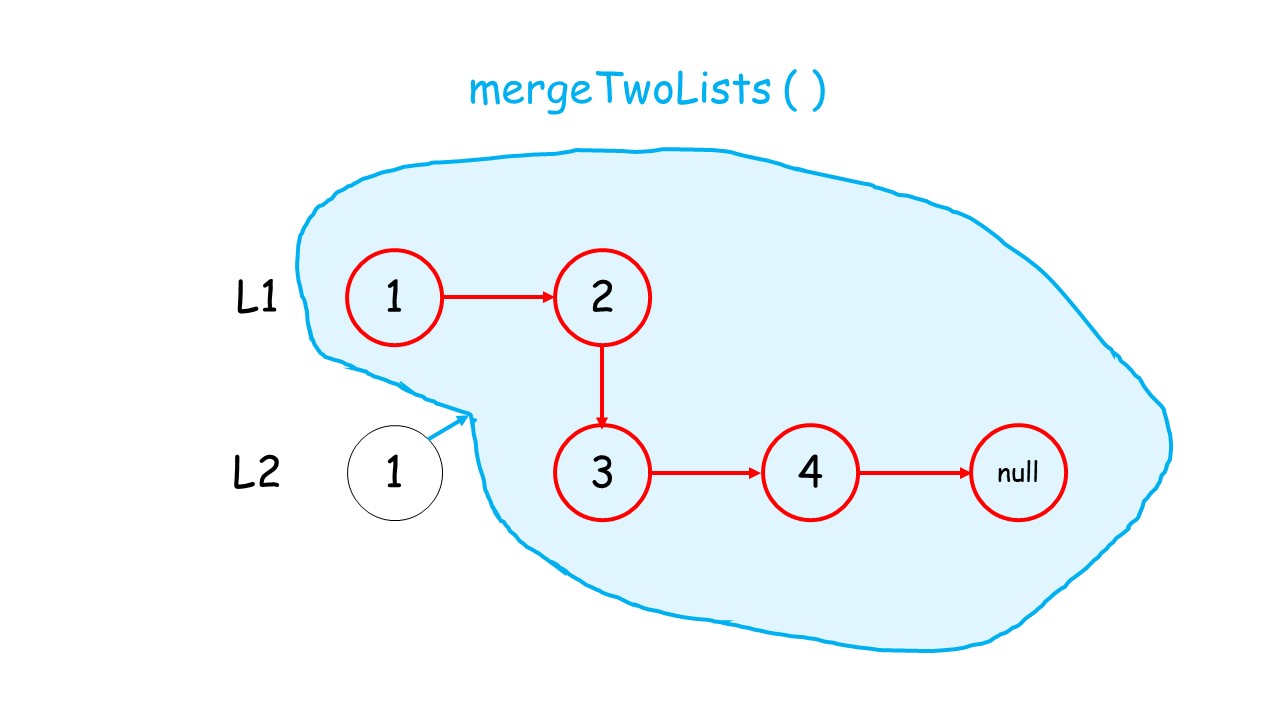
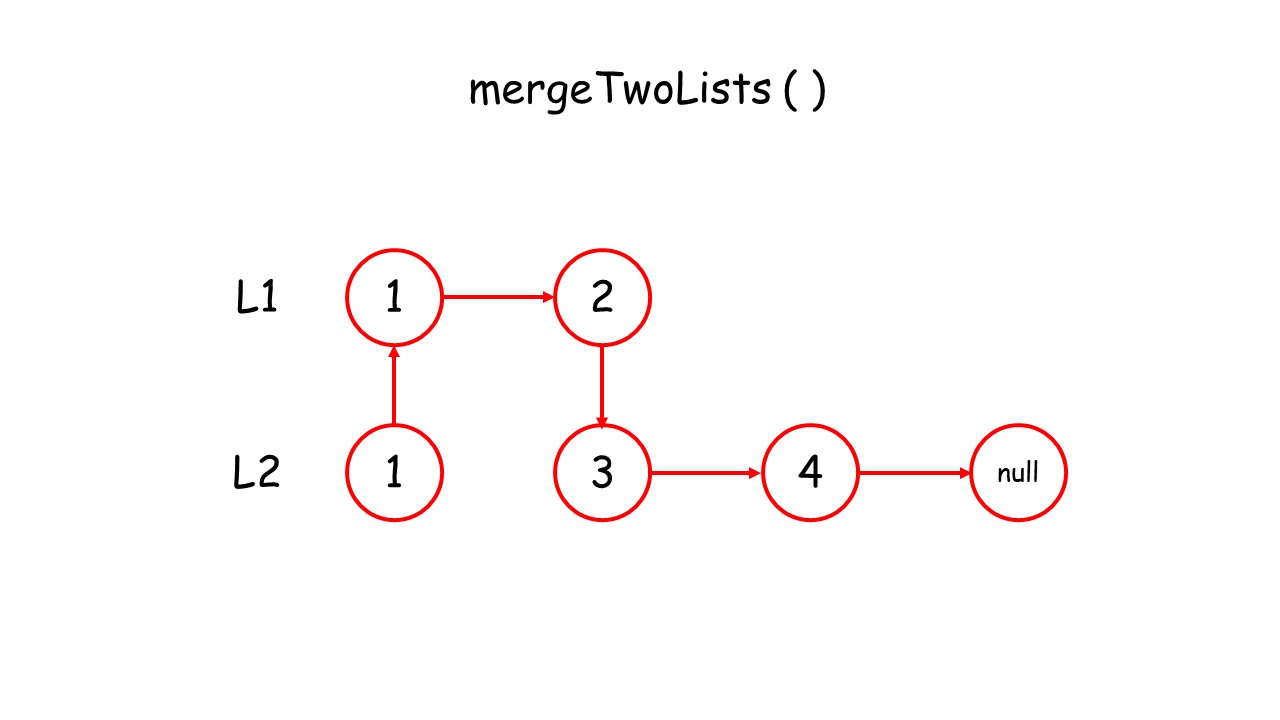
//递归调用合并升序链表
/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {//终止条件 list1.list2有一个遍历到null就终止条件if(list1 == NULL)return list2;if(list2 == NULL)return list1;//递归条件if(list1->val<list2->val){list1->next = mergeTwoLists(list1->next,list2);return list1;//有返回类型，就要返回}else{list2->next = mergeTwoLists(list1,list2->next);return list2;}}
};

但是这里出现了一个问题，就是递归的空间复杂度不是o(1)

递归算法的空间复杂度_递归的空间复杂度-CSDN博客

递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度 1*n

递归算法的时间复杂度=每次递归的时间复杂度递归次数 12^n

归并排序：此方法时间复杂度 O(nlogn)O(nlogn)O(nlogn)，空间复杂度 O(1)O(1)O(1)。

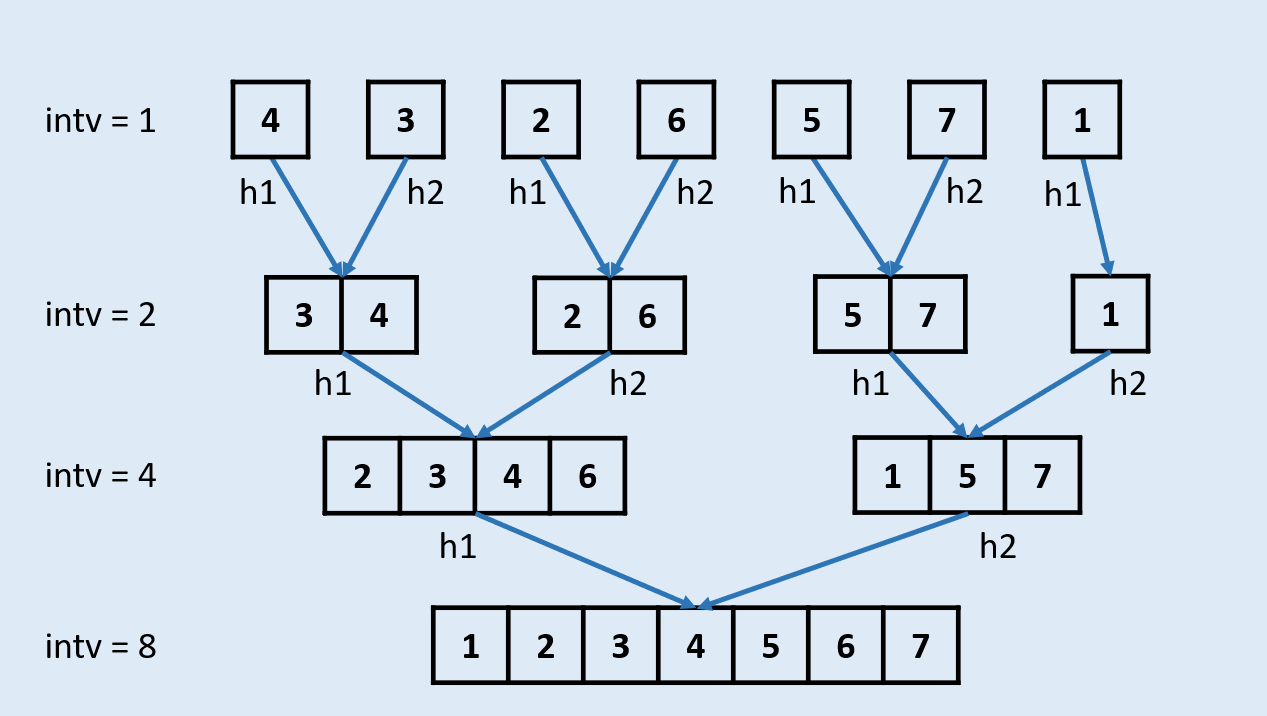
【138】随机链表的复制

方法1：空间复杂度O(N):哈希表使用线性大小的额外空间。

时间复杂度O(N):两轮遍历链表，使用O(N)时间。

/*
// Definition for a Node.
class Node {
public:int val;Node* next;Node* random;Node(int _val) {val = _val;next = NULL;random = NULL;}
};
*/class Solution {
public:Node* copyRandomList(Node* head) {Node* cur = head;unordered_map<Node*,Node*> listmp;//当前链表 排序后链表while(cur != NULL){listmp[cur] = new Node(cur->val);//能存储丰富的指针信息cur = cur->next;}cur = head;//重新回到链表头//构建新链表的next和ramdom指向while(cur != NULL){listmp[cur]->next  = listmp[cur->next];//真的好牛，都不用拿出来操作listmp[cur]->random = listmp[cur->random];cur = cur->next;}return listmp[head];}
};

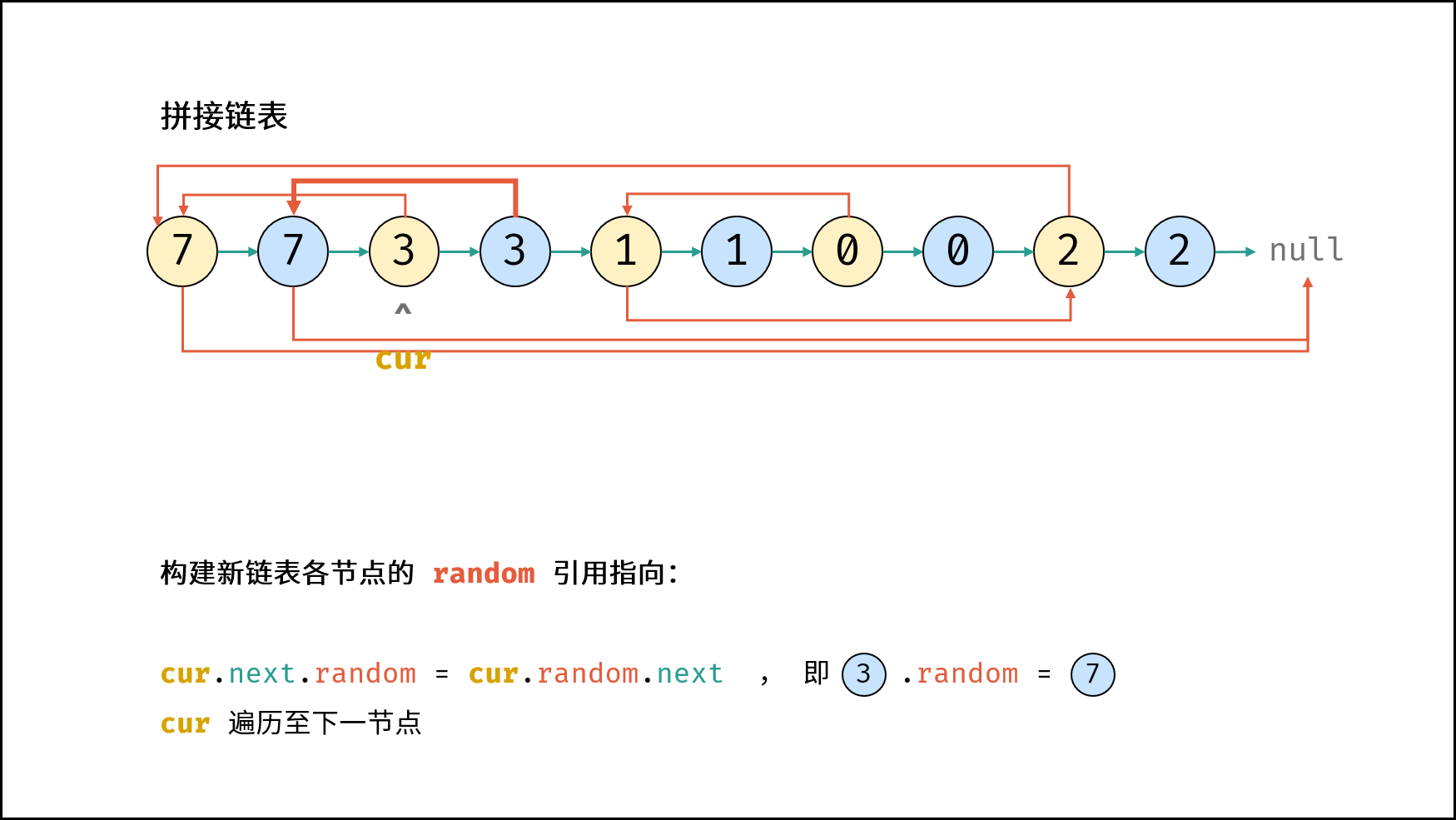
方法二：拼接+拆分

/*
// Definition for a Node.
class Node {
public:int val;Node* next;Node* random;Node(int _val) {val = _val;next = NULL;random = NULL;}
};
*/class Solution {
public:Node* copyRandomList(Node* head) {//方法2：拼接 拆分链表//原节点1->新节点1->原节点2->新节点2...拼接链表if(head == NULL) return NULL;Node* cur = head;//复制各个节点，并且构建拼接链表while(cur!=NULL){Node* tmp = new Node(cur->val);tmp->next = cur->next;cur->next = tmp;cur = tmp->next;}// 2. 构建各新节点的 random 指向cur = head;while(cur != nullptr) {if(cur->random != nullptr)cur->next->random = cur->random->next;//太牛了，又转回来了cur = cur->next->next;}// 3. 拆分两链表cur = head->next;Node* pre = head, *res = head->next;while(cur->next != nullptr) {pre->next = pre->next->next;cur->next = cur->next->next;pre = pre->next;cur = cur->next;}pre->next = nullptr; // 单独处理原链表尾节点return res;      // 返回新链表头节点}
};

【203】移除链表元素

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeElements(ListNode* head, int val) {ListNode* dummyHead = new ListNode(0, head);ListNode* temp = dummyHead;while (temp->next) {if (temp->next->val == val) {temp->next = temp->next->next;} else {temp = temp->next;}}return dummyHead->next;}
};

上面的做法没有手动释放内存，这样不利于内存管理!!

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeElements(ListNode* head, int val) {ListNode* dummyHead = new ListNode(0);//设置一个虚拟头结点dummyHead->next = head;//将虚拟头结点指向head头结点，方便头结点做删除操作ListNode* cur = dummyHead;//现在的节点从虚拟头节点开始while(cur->next != NULL){//因为有虚拟头结点，一切操作都延后一位if(cur->next->val == val){//删除ListNode* tmp = cur->next;//存储临时删除结点cur->next = cur->next->next;delete tmp;// 释放该删除的结点}else{cur = cur->next;}}head = dummyHead->next;//舍去虚拟头结点delete dummyHead;return head;}
};

【206】反转链表

双指针法

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {ListNode* cur = head;//当前节点指向头结点ListNode* pre = NULL;//双指针ListNode* tmp;while(cur){//如果cur是NULL就出错啦tmp = cur->next;//存储下一个结点cur->next = pre;//改变指向pre = cur;//Pre移动到curcur = tmp;//cur移动到cur->next}return pre;}
};

时间复杂度o(n),空间复杂度o(1)。

！！【707】设计链表

单链表中的节点应该具备两个属性：val 和 next 。val 是当前节点的值，next 是指向下一个节点的指针/引用。

如果是双向链表，则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。

实现 MyLinkedList 类：

MyLinkedList() 初始化 MyLinkedList 对象。
int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。
void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点。
void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。
void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将 不会插入 到链表中。
void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的节点。

输入
["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"]
[[], [1], [3], [1, 2], [1], [1], [1]]
输出
[null, null, null, null, 2, null, 3]解释
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addAtHead(1);
myLinkedList.addAtTail(3);
myLinkedList.addAtIndex(1, 2);    // 链表变为 1->2->3
myLinkedList.get(1);              // 返回 2
myLinkedList.deleteAtIndex(1);    // 现在，链表变为 1->3
myLinkedList.get(1);              // 返回 3

class MyLinkedList {
public:struct ListNode{int val;ListNode* next;ListNode(int x):val(x),next(NULL){};};MyLinkedList() {//构造函数dummyhead = new ListNode(0);//初始化size = 0;//初始化}//注意cur到底取dummyhead,还是取dummyhead->nextint get(int index) {//5.获取链表中下标为 index 的节点的值。if(index<0 || index >size-1){//小标不能小于零 也不能越界return -1;}ListNode* cur = dummyhead->next;//索引是从head：0开始记，dummyhead不参与引用while(index--){cur = cur->next;}return cur->val;}void addAtHead(int val) {//1.将一个值为 val 的节点插入到链表中第一个元素之前。ListNode* node= new ListNode(val);//先定义一个新节点存储val值node->next = dummyhead->next;//先尾部指向dummyhead->next = node;//后头部被指size++;//增加了结点}void addAtTail(int val) {//2.将一个值为 val 的节点追加到链表中作为链表的最后一个元素。ListNode* node = new ListNode(val);//定义一个新结点存储val值,结点后指向NULLListNode* cur = dummyhead;//不是dummynode->next，防止空链表的情况while(cur->next!=NULL){//遍历链表，不能用size,会改变size的值cur = cur->next;//遍历到最后}cur->next = node;size++;}//3.将一个值为 val 的节点插入到链表中下标为 index 的节点之前。//如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。//如果 index 比长度更大，该节点将 不会插入 到链表中。void addAtIndex(int index, int val) {if(index > size)return;//数组下标 0,1.. size是0,1,2...（只有dummyhead，size=0）if(index<0)return;ListNode* node = new ListNode(val);//定义新结点存储valListNode* cur = dummyhead;//为什么这里和get不一样：cur要在插入结点之前while(index--){cur = cur->next;}node->next = cur->next;cur->next = node;size++;}void deleteAtIndex(int index) {//4.if(index<0 || index >size-1){//小标不能小于零 也不能越界return;}ListNode* cur = dummyhead;while(index--){cur = cur->next;}ListNode* tmp = cur->next;cur->next = cur->next->next;delete(tmp);size--;}private:int size;//定义链表大小ListNode* dummyhead;//定义虚拟头结点
};/*** Your MyLinkedList object will be instantiated and called as such:* MyLinkedList* obj = new MyLinkedList();* int param_1 = obj->get(index);* obj->addAtHead(val);* obj->addAtTail(val);* obj->addAtIndex(index,val);* obj->deleteAtIndex(index);*/

增加打印链表功能，还有就是在ACM模式下验证，捋清楚什么时候是cur = dummyhead->next;

cur = dummyhead->next：当我们int get(int index)时，因为dummyhead没有索引，所以可以直接从head开始设置。

但是在之后 void addAtTail(int val)， void addAtIndex(int index, int val) ，void deleteAtIndex(int index)的情况下，要对链表进行增删操作，需要提前一个结点，所以此时就直接让cur = dummyhead。

【19】删除链表的倒数第N个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

要删除倒数第n个结点，需要在倒数第n+1(前一个结点处)进行删除。所以fast和slow指针需要间隔n+1位置。先让fast指针在n+1处，再同时把fast和slow指针向后移，整个操作用到的时间复杂度是o(n),空间复杂度o(1)。

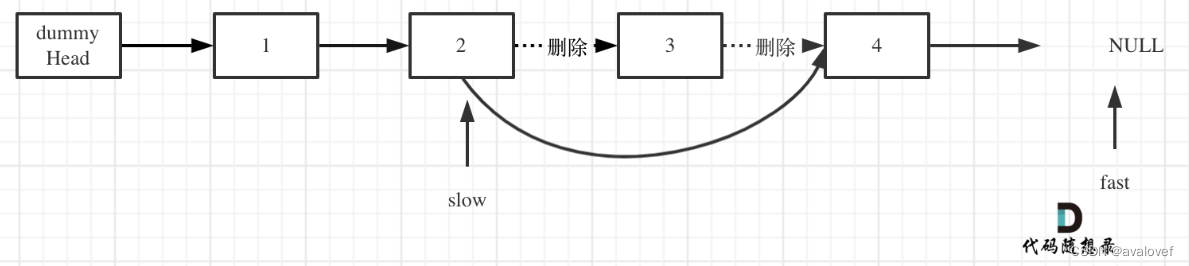
在这里插入图片描述

示例 1：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* dummyhead = new ListNode(0);dummyhead->next = head;ListNode* cur = dummyhead;ListNode* pre = dummyhead;int size = 0;while(n-- && cur != NULL){//cur和pre间隔n步cur = cur->next;}cur = cur->next;//cur还要再走一步，删除需要在结点的上一个结点while(cur!=NULL){cur = cur->next;pre = pre->next;}//经典的删除结点操作ListNode* tmp = pre->next;pre->next = pre->next->next;delete(tmp);return dummyhead->next;}
};

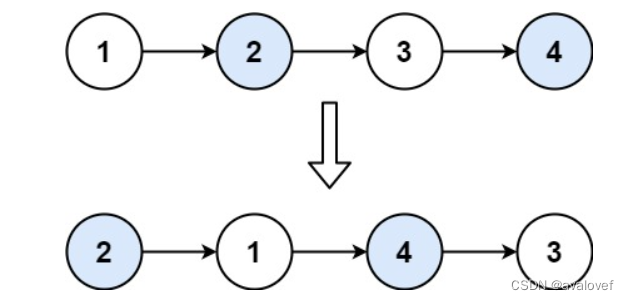
【24】两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。
在这里插入图片描述

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {ListNode* dummyhead = new ListNode(0);dummyhead->next = head;ListNode* cur = dummyhead;ListNode* tmp;ListNode* tmp1;while(cur->next!=NULL && cur->next->next!=NULL){tmp = cur->next;cur->next = cur->next->next;//步骤一tmp1 = cur->next->next;cur->next->next = tmp;//步骤二tmp->next = tmp1;//步骤三cur = cur->next->next;}return dummyhead->next;}
};

【92】反转链表II

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseBetween(ListNode* head, int left, int right) {ListNode* dummyhead = new ListNode(0);dummyhead->next = head;ListNode* tmp;ListNode* tmp1;ListNode* leftnode = dummyhead;ListNode* rightnode = dummyhead;while(leftnode!= NULL && leftnode->val != left){tmp = leftnode;//保存的是leftnode的前一个结点leftnode = leftnode->next;}while(rightnode!=NULL && rightnode->val != right){rightnode= rightnode->next;}tmp1 = rightnode->next;//保存rightnode下一个结点//翻转链表 双指针法ListNode* tmp2;//第三个结点ListNode* pre = tmp;//第一个结点ListNode* cur = leftnode;//第二个结点while(cur != tmp1){tmp2 = cur->next;cur->next = pre;pre = cur;cur = tmp2;}tmp->next = cur;leftnode->next = tmp1;return dummyhead->next;}
};

【160】相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交**：**

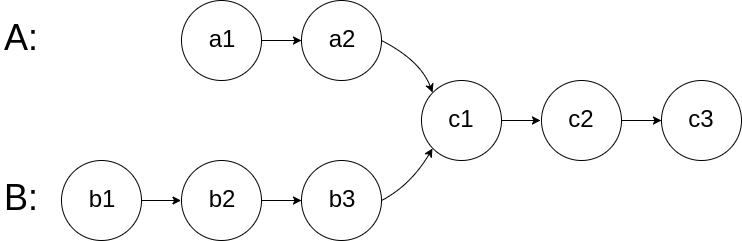
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {//快慢指针 要保证链式结构不变就令取变量ListNode* Aptr = headA;ListNode* Bptr = headB;while(Aptr!=Bptr){Aptr = Aptr == NULL? headA:Aptr->next;//如果没碰到就从头再来，因为速度不一样总会碰上Bptr = Bptr == NULL? headB:Bptr->next;}return Aptr;}
};

【141】环形链表

给你一个链表的头节点 head ，判断链表中是否有环。如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。如果链表中存在环 ，则返回 true 。否则，返回 false 。

进阶：用o(1)常量内存解决此问题。

因为才做了哈希表，所以环形链表的题目我认为可以用哈希表存储每个结点的值，到环形链表时，第一个find的结点值就是环开始的位置。但是这样的内存肯定是很大的。第二种方法是快慢指针，快慢指针在环处必定会相遇，这种内存就不会很大。

class Solution {
public:bool hasCycle(ListNode *head) {unordered_set<ListNode*> list_set;//存储结点值while(head != NULL){if(list_set.count(head)){//出现过这个元素就返回1return true;}else{//没有出现过就存储list_set.insert(head);head = head->next;}}return false;//不是环形链表最后指针会指向NULL(要是不在意这个HEAD值的话可以直接看是否是NULL)}
};

另外一种是快慢指针的方式：

class Solution {
public:bool hasCycle(ListNode *head) {if(head==NULL||head->next ==NULL)return false;ListNode* fast = head->next;ListNode* slow = head;while(fast!=slow){//当快指针没有追上慢指针的时候if(fast != nullptr && fast->next != nullptr) {fast = fast->next->next;slow = slow->next;}else return false;}return true;}
};

【142】环形链表II

同上面一道题，只是需要我们返回进入环形链表的第一个结点。所以我们也可以用哈希表或者快慢指针的方式来做。

**哈希表做的话，由于是无序的，所以第一个被查找的结点就是一个入环的结点。**就很牛逼！

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {unordered_set<ListNode*> set;//定义setwhile(head!=NULL){if(set.find(head)!=set.end()){//找到了return head;}else{set.insert(head);head = head->next;}}return NULL;}
};

快慢指针相遇的位置不一定是在入环的第一个结点处，所以两个指针相遇以后还要再返回一定的距离去找入环的地方：

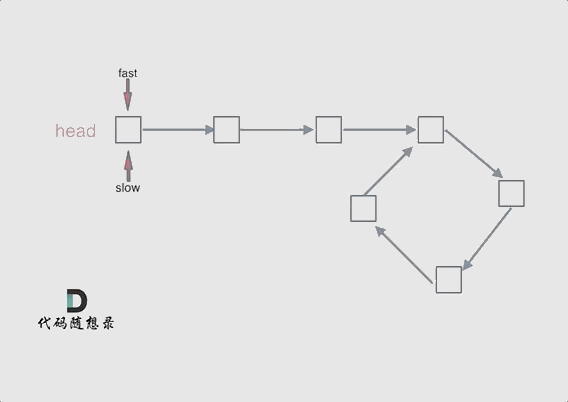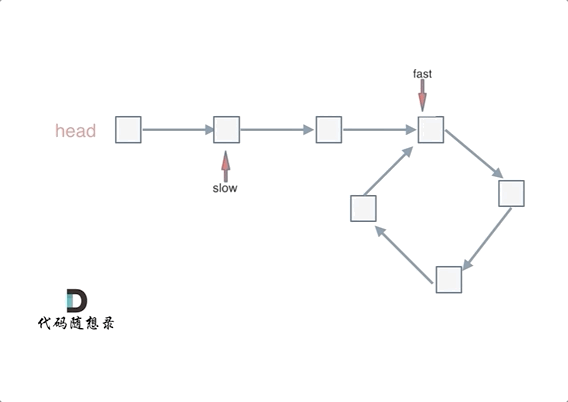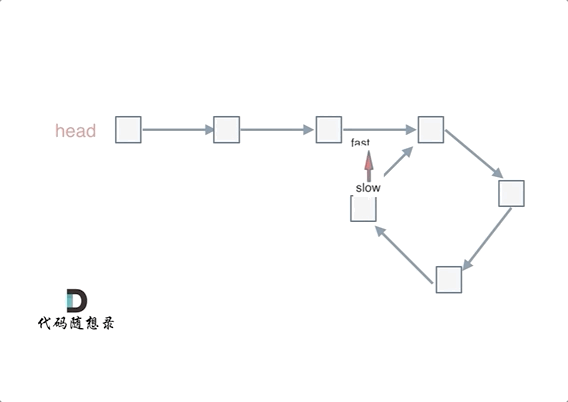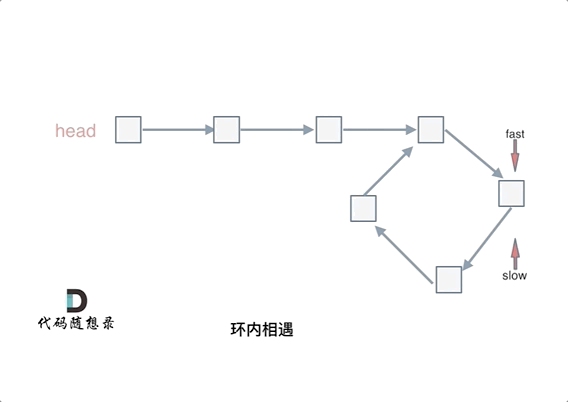
141.环形链表

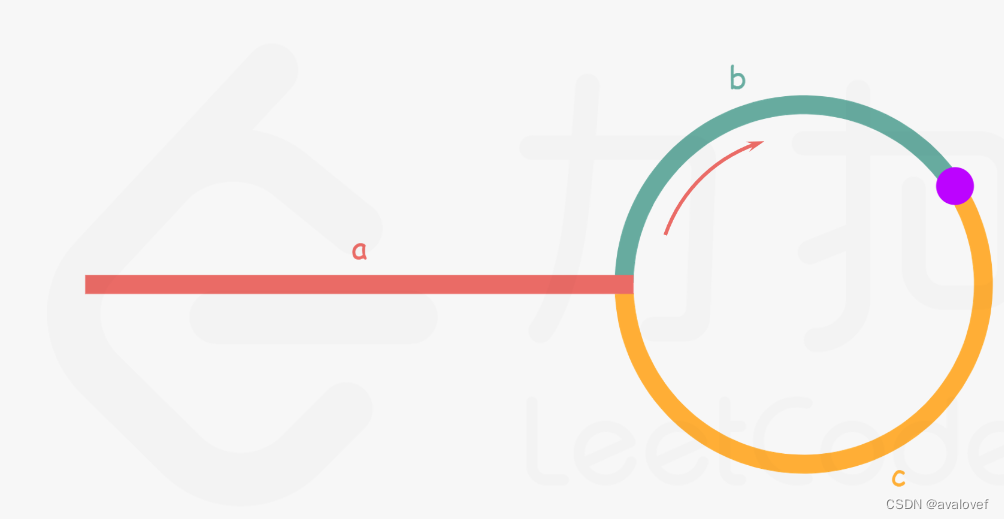
在这里插入图片描述

忽略fast指针和slow指针两者重复走的圈数，那么slow指针走的步数为：a+b。fast指针走的步数为a+b+n(b+c)。可以在代码里设定fast指针走两步，slow指针每次走一步，那么有fast指针步数 = 2*slow指针步数。则有2x(a+b) =a+b+nx(b+c) —>由于我们求的是入口的结点—>需要a------->a =(n-1)(b+c)+c (n>=1)fast指针至少要比slow指针多走一圈。

当n= 1的时候，a=c,意味着一个指针从头结点出发，从相遇的结点也出发一个指针，这两个指针每次都只走一个结点，那么当这两个指针相遇的时候，就是环形入口的结点。同理n>1,相当于fast在环里面多跑了n圈。如下图所示：

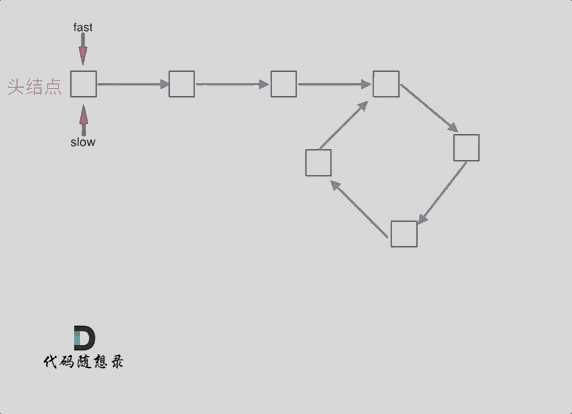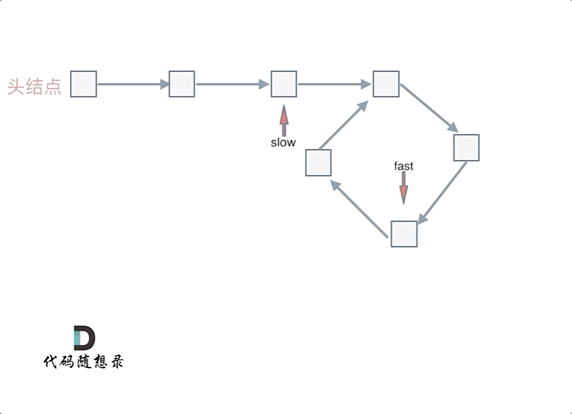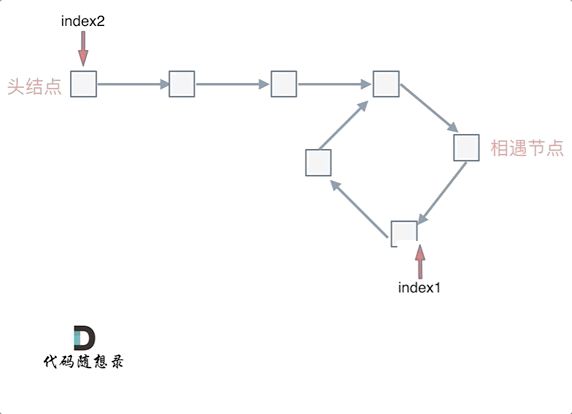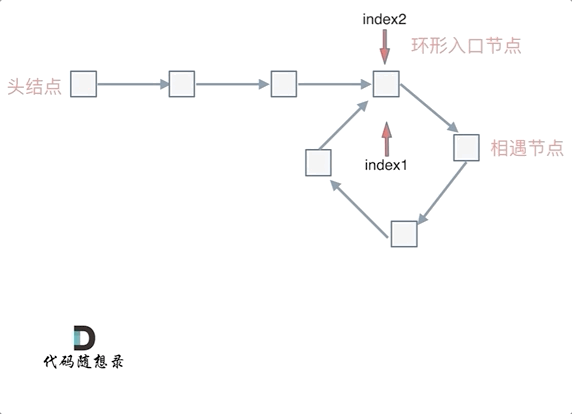
142.环形链表II（求入口）

所以这道题的核心就是在环内的相遇结点处，指派两个指针，一个从head走，一个从当前相遇结点走，他们相遇的地方一定是环的入口结点。

class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* fast =head;ListNode* slow =head;ListNode* prev1 = head;ListNode* prev2;while(fast != NULL && fast->next!=NULL){//两个条件都要满足fast = fast->next->next;//先移动再判断    slow = slow->next;if(slow == fast){prev2 = fast;while(prev1 != prev2){prev1 = prev1->next;prev2 = prev2->next;}return prev1;}}return NULL;}
};

循环链表解决约瑟夫问题：约瑟夫问题 C++求解_c++约瑟夫问题_MilkLeong的博客-CSDN博客

【876】链表的中间结点

给你单链表的头结点 head ，请你找出并返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。

步骤：首先遍历整个链表，求出index，再返回

class Solution {
public:ListNode* middleNode(ListNode* head) {int index =0;//定义链表下标ListNode* prev = head;while(prev!=NULL){index++;prev = prev->next;}if(index%2 ==0){//偶数index = index/2;while(index--){head = head->next;}}else{//奇数index = index/2;while(index--){head = head->next;}}return head;}
};

快慢指针：每次快指针比慢指针多走两步，则快指针到链表末尾的时候，慢指针正好在中间的位置。(奇数链表在中间，偶数链表在靠前的中间结点)。

ListNode* endOfFirstHalf(ListNode* head){ListNode* fast = head;ListNode* slow = head;while(fast->next!=NULL && fast->next->next!=NULL){fast = fast->next->next;slow = slow->next;}return slow;
}

【86】分隔链表

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在 大于或等于 x 的节点之前。你应当保留两个分区中每个节点的初始相对位置。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* middleNode(ListNode* head) {int index =0;//定义链表下标ListNode* prev = head;while(prev!=NULL){index++;prev = prev->next;}index = index/2;while(index--){head = head->next;}return head;}
};

【21】合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
//双指针
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {ListNode* dummyhead = new ListNode(-1);//定义虚拟头结点ListNode* prev = dummyhead;//定义临时结点while(list1!=NULL && list2!=NULL){if(list1->val>list2->val){prev->next = list2;list2 = list2->next;}else{prev->next = list1;list1 = list1->next;}prev = prev->next;}// 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可prev->next = list1 == nullptr ? list2 : list1;dummyhead = dummyhead->next;return dummyhead;//preHead和 prev公用一个地址}
};//递归
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(list1 == NULL)return list2;if(list2 == NULL)return list1;if(list1->val <list2->val){list1->next = mergeTwoLists(list1->next, list2);return list1;}else{list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};

【23】合并K个升序排序

给你一个链表数组，每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中，返回合并后的链表。(lists中的子集个数是不定的)。

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[1->4->5,1->3->4,2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

这道题跟上道题类似，但是合并的链表要比上个的多,相当于上道题是这道题的子集。可知，合并两个有序链表可以使用迭代或者递归来完成。容易想到，对于合并K个链表，可以从头开始两两合并。时间复杂度 O(kn) ，空间复杂度 O(1)

class Solution {
public://递归调用ListNode* merge(ListNode* p1,ListNode* p2){if(!p1)return p2;if(!p2)return p1;if(p1->val<=p2->val){p1->next = merge(p1->next, p2);return p1;}else{p2->next = merge(p1, p2->next);return p2;}}ListNode* mergeKLists(vector<ListNode*>& lists) {if(!lists.size())return NULL;ListNode* head =lists[0];for(int i =1;i<lists.size();i++){if(lists[i]){head = merge(head,lists[i]);}}return head;}
};

!【234】回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

最开始我想的是，翻转链表然后与原链表进行比较（快慢指针法），但是在测试的过程中发现，始终过不了[1,1,2,1]这个测试案例，然后调试的时候发现这样做是会该变原始的head的（共用地址），翻转以后的reverlist和head已经变了：head是跟cur一起共用地址了。head和cur是共用地址的，所以最后head也要被改变，这样并不能进行比较。

要用快慢指针，正确的做法是，我们可以将链表的后半部分反转（修改链表结构），然后将前半部分和后半部分进行比较。比较完成后我们应该**将链表恢复原样。**虽然不需要恢复也能通过测试用例，但是使用该函数的人通常不希望链表结构被更改。

该方法虽然可以将空间复杂度降到o(1),但是在并发环境下，该方法也有缺点，在并发环境下，函数运行的时候需要锁定其他线程或对进程对链表的访问，因为函数在执行过程中链表是会被修改的。

整个流程可以分为以下五个步骤：

1.找到前半部分链表的尾结点（找到中间结点）。2.翻转后半部分的链表 3.判断是否回文 4.恢复链表5.返回结果

class Solution {
public:bool isPalindrome(ListNode* head) {if (head == nullptr) {return true;}// 找到前半部分链表的尾节点并反转后半部分链表ListNode* firstHalfEnd = endOfFirstHalf(head);ListNode* secondHalfStart = reverseList(firstHalfEnd->next);// 判断是否回文ListNode* p1 = head;ListNode* p2 = secondHalfStart;bool result = true;while (result && p2 != nullptr) {if (p1->val != p2->val) {result = false;}p1 = p1->next;p2 = p2->next;}        // 还原链表并返回结果firstHalfEnd->next = reverseList(secondHalfStart);return result;}ListNode* reverseList(ListNode* head) {//翻转链表ListNode* prev = nullptr;ListNode* curr = head;while (curr != nullptr) {ListNode* nextTemp = curr->next;//临时变量存储下一个结点curr->next = prev;prev = curr;curr = nextTemp;}return prev;}ListNode* endOfFirstHalf(ListNode* head) {//返回后半截的第一个结点 [1,2,2,1] 则是返回 [2,2,1]ListNode* fast = head;ListNode* slow = head;while (fast->next != nullptr && fast->next->next != nullptr) {fast = fast->next->next;slow = slow->next;}return slow;}
};

class Solution {
public:ListNode* reverseList(ListNode* head){//翻转链表ListNode* cur = head;ListNode* pre = NULL;ListNode* tmp;//保存临时结点while(cur){tmp = cur->next;//保存cur之后的结点cur->next = pre;pre = cur;cur = tmp;}return pre;//返回一定是pre，cur已经指向NULL了}ListNode* FindMiddleNode(ListNode* head){//找到中间结点ListNode* midnode = head;ListNode* tmp = head;int index =0;while(midnode && midnode->next){//不要改变head的结构tmp = tmp->next;index++;}index = index/2;while(index--){midnode = midnode->next;}return midnode;}bool isPalindrome(ListNode* head) {      if(!head)return true;ListNode* tmphead = head;ListNode* reverlist;reverlist = reverseList(FindMiddleNode(tmphead));while(head != NULL){if(head->val != reverlist->val){//tmphead = FindMiddleNode(tmphead);return false;}else{head = head->next;reverlist = reverlist->next;}} // tmphead = FindMiddleNode(tmphead);return true;}
};