图神经网络(GNNs)是一类强大的深度学习(DL)模型,用于对相互连接的图数据集进行分类和回归。它们已被用于研究人类互动、分析蛋白质结构、设计化合物、发现药物、识别入侵机器、模拟单词之间的关系、寻找有效的交通路线等。许多成功的GNN模型已被提出,例如图卷积网络(GCN)、图注意力网络(GAT)、图同构网络(GIN)和消息传递神经网络(MPNN)。这些模型都是基于“普通图”数据模型,其中关系是二元关系,即只定义在顶点对之间。普通图无法充分捕捉数据中编码的关系。例如,在合作作者关系方面,三个人合作完成一篇论文和每两个人合作完成不同论文的情况,在普通图中无法区分,因为它们都被建模为三个顶点的完全图。其他领域也存在类似的问题,例如社交网络、药物相互作用网络、神经科学和生态学。
为了捕捉这样的关系,需要超越成对交互。高阶图数据模型(HOGDMs)通过在图数据模型(GDM)中显式编码多边交互来解决这个问题。常见的 HOGDM 包括超图(HG)、单纯形复形(SC)或细胞复形(CC)。HOGNN 利用 HOGDM 中的多元关系,在 GNN 模型中取得了比基于普通图的 GNN 模型更强大的表现。
许多 HOGNN 模型已经被提出,它们具有不同的神经网络架构和不同的“高阶”概念。由于这种多样性,很难分析和比较 HOGNN 模型,并决定在什么情况下使用特定的模型。本文使用分类体系研究了100多个与HOGNN相关的方案,并讨论了它们的表达能力、时间复杂度和应用,将有助于设计更强大的未来GNNs。
1 为什么需要高阶图神经网络 (HOGNN)
传统的图神经网络(GNNs)在许多图任务中取得了令人瞩目的成果,但它们也面临着一些挑战。高阶图神经网络(HOGNNs)作为一种新兴的GNN模型,通过引入多阶关系来增强模型的表示能力和预测精度,有效地解决了传统GNNs的局限性。
1.1 传统GNNs的局限性
1.3 HOGNN提升模型表达能力
2 分类法与蓝图
分类法和蓝图共同提供了一个全面的框架,用于理解和构建各种HOGNN模型,并帮助研究人员根据特定任务选择合适的模型。
2.1 分类法
2.1.1 图数据模型 (HOGDMs)
2.1.1.1 基础元素
2.1.1.2 已建立的HOGDMs
2.1.1.3 新的HOGDMs
2.1.2 高阶图神经网络架构 (HOGNN Architectures)
指定HOGNN架构的核心部分是确定将在GNN层中使用的传讯通道。
2.2 蓝图
蓝图提供了一个构建HOGNN模型的步骤指南:
2.2.1 选择HOGDM
根据需要捕获的图结构选择合适的HOGDM,例如选择超图来表示多阶关系,选择细胞复形来表示复杂的多维结构。
2.2.2 指定HOGNN细节
2.2.3 构建HOGNN模型
根据蓝图和分类法,使用所选的HOGDM和HOGNN细节构建具体的HOGNN模型。
3 高阶图数据模型 (HOGDM)
高阶图数据模型 (HOGDM) 是一种扩展了传统图数据模型 (GDM) 的数据结构,能够更有效地表示和处理包含多阶关系的图数据。
3.1 HOGDM的组成元素
3.1.1 链接 (Links)
将图中的实体(节点、边、子结构等)连接起来。HOGDM的链接类型与GDM不同,例如:
3.1.2 邻接 (Adjacencies)
指定实体之间如何连接。HOGDM的邻接概念比GDM更丰富,例如:
3.1.3 区分的子结构 (Distinguished Substructures)
指定图中的特定子结构,例如子图、子图元组、模式等。这些子结构可以具有自己的特征向量,并在GNN层中被更新。
3.1.4 附加信息 (Additional Information)
与实体或子结构相关联的额外信息,例如顶点所属的三角形数量。
3.1.5 嵌套 (Nesting)
将图或超图作为更高层次图中的节点。例如,分子中的每个原子可以作为一个节点,而原子之间的化学键可以作为连接这些节点的超边。
3.2 常见的HOGDM类型
4 高阶图神经网络 (HOGNN) 架构
高阶图神经网络 (HOGNN) 架构是利用高阶图数据模型 (HOGDM) 进行图学习的一种模型。HOGNN 架构通过引入多阶关系,能够更有效地表示和处理图中的复杂结构,从而提高模型的预测精度和表达能力。
4.1 HOGNN 架构的组成元素
4.2 常见的 HOGNN 架构类型
4.2.1 基于超图的 HOGNN
4.2.2 基于单纯复形的 HOGNN
基于边界邻域的 MP: 使用节点和边界超边之间的边界关系来定义 MP 通道,例如 MPSN 和 SAT。
4.2.3 基于细胞复形的 HOGNN
基于边界邻域的 MP: 使用节点和边界细胞之间的边界关系来定义 MP 通道,例如 CW Networks 和 CCNN。
4.2.4 基于节点元组集合图的 HOGNN
基于下邻域的 MP: 使用节点元组之间的下邻域关系来定义 MP 通道,例如 k-GNN 和 k-IGN。
4.2.5 基于子图集合图的 HOGNN:
4.2.6 基于模式图的 HOGNN
4.2.7 基于嵌套图数据模型的 HOGNN
基于ego网络的 MP: 使用节点的嵌套ego网络来定义 MP 通道,例如 NGNN。
4.2.8 基于其他HOGDM的HOGNN
4.3 HOGNN 架构的设计考虑因素
4.4 HOGNN 架构的优势
5 高阶图神经网络 (HOGNN) 表达能力
HOGNN 的表达能力是指其能够学习到的图结构信息的丰富程度。HOGNN 通过引入多阶关系和复杂的图结构,能够学习到比传统 GNN 更丰富的图结构信息,从而提高模型的预测精度和泛化能力。
5.1 表达能力的衡量指标
5.2 影响表达能力的因素
5.3 HOGNN 表达能力的优势
5.4 HOGNN 表达能力的挑战
6 未来机遇
6.1 探索新的 HOGDM
6.2 探索新的 HOGNN 模型
6.3 开发高效的 HOGNN 处理框架
6.4 探索 HOGNN 的硬件加速
6.5 探索 HOGNN 的全局公式
6.6 探索时间 HOGNN
6.7 探索图压缩和摘要
6.8 将 HOGNN 集成到大型语言模型 (LLM) 流程中
- 无法区分复杂的图结构: 传统的GNNs基于二阶关系,即只关注节点对之间的连接。然而,许多现实世界的图数据中存在着更复杂的结构,例如三元组、群组、子图等。这些结构无法用传统的GNNs准确表示,导致模型无法区分非同构的图,例如下图: 两个图 G1 和 G2 具有相同的 1-跳邻居,但结构不同。G1 包含两个三角形,而 G2 不包含。传统的GNNs无法区分这两个图,因为它们将它们视为同构的。
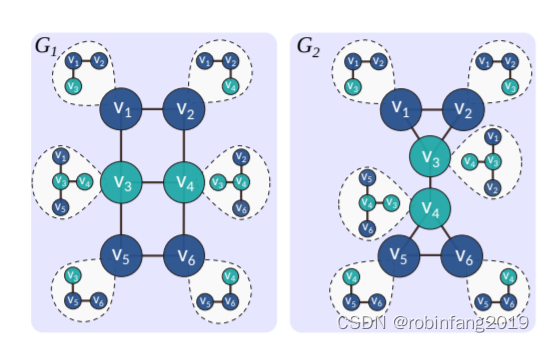
- 无法捕捉高阶关系: 传统的GNNs无法有效地捕捉节点之间更复杂的关系,例如群体结构、协同作用等。例如,在社会网络中,一组朋友之间可能存在更复杂的多阶关系,而传统的GNNs无法准确地捕捉这些关系。
-
1.2 HOGNN提高预测精度
- 消除过度平滑和过度压缩问题: 传统的GNNs在处理大型图数据时容易出现过度平滑或过度压缩的问题,导致模型无法捕捉到图中细粒度的信息。HOGNNs通过引入多阶关系,可以更好地捕捉图中不同层次的结构信息,从而提高模型的预测精度。
- 增强特征表示: HOGNNs可以学习到更丰富的节点和边特征表示,从而更好地理解图中的复杂关系。例如,HOGNNs可以学习到每个节点所属的群组特征、子图特征等,从而更准确地预测节点的属性或标签。
- 区分更复杂的图结构: HOGNNs可以区分传统GNNs无法区分的非同构图,例如具有不同群组结构或子图结构的图。这使得HOGNNs在图分类、图聚类等任务中具有更高的表达能力。
- 学习更复杂的函数: HOGNNs可以学习到更复杂的函数,例如可以预测图中任意子图的属性或标签。这使得HOGNNs在图推理、图生成等任务中具有更高的表达能力。
- 链接 (Links): 将图中的实体(节点、边、子结构等)连接起来。例如,普通图中的链接是边,超图中是超边,细胞复形中是细胞。

- 邻接 (Adjacencies): 指定实体之间如何连接。例如,普通图中的邻接由边完全确定,而超图中可以基于顶点和超边的共享程度进行邻接。
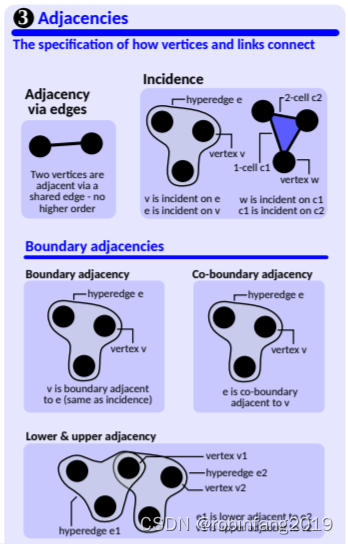
- 区分的子结构 (Distinguished Substructures): 指定图中的特定子结构,例如子图、子图元组、模式等。
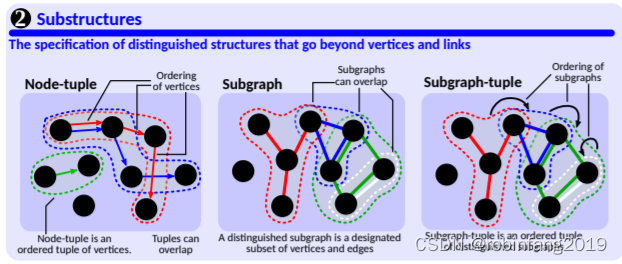
- 附加信息 (Additional Information): 与实体或子结构相关联的额外信息,例如顶点所属的三角形数量。
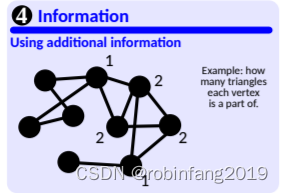
- 嵌套 (Nesting): 将图或超图作为更高层次图中的节点。
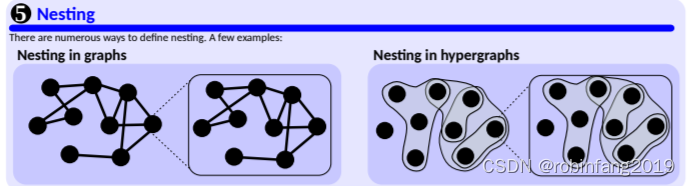
- 超图 (Hypergraph, HG): 使用超边来表示多阶关系。
- 单纯复形 (Simplicial Complex, SC): 限制超图的定义,确保子集也形成超边,例如社交网络中的群组。
- 细胞复形 (Cell Complex, CC): 进一步扩展SC,允许形成更高维的子结构,例如分子中的环。
- 节点元组集合图 (Node-Tuple Collection Graph, NT-Col-Graph): 使用有序的节点元组来表示多阶关系。
- 子图集合图 (Subgraph Collection Graph, SCol-Graph): 使用子图集合来表示图中的结构信息。
- 子图元组集合图 (Subgraph-Tuple Collection Graph, ST-Col-Graph): 类似于SCol-Graph,但使用子图元组来表示更复杂的结构。
- 模式图 (Motif-Graph): 使用模式来定义邻接关系,例如三角形。
- 子图计数图 (Subgraph Count Graph, SCnt-Graph): 将子图数量作为附加信息。
- 嵌套图数据模型 (Nested Graph Data Model): 将子图或超图作为更高层次图中的节点。
- 消息传递 (Message Passing, MP) 通道: 指定GNN层中用于交换信息的通道类型,例如卷积、注意力或通用消息传递。
- 局部 vs. 全局公式: 指定MP通道的构建方式,例如局部公式(基于单个节点)或全局公式(基于整个图)。
- 多跳通道: 指定连接多个跳步的节点的通道,用于捕捉更远距离的关系。
- 嵌套: 指定将图或超图作为更高层次图中的节点的机制。
- 构建MP通道: 选择MP通道的类型,例如卷积、注意力或通用消息传递,并指定通道的连接方式,例如局部连接或全局连接。
- 特征变换: 指定如何在不同GNN层之间转换特征向量。
- 提升和降低: 指定如何将输入的普通图转换为HOGDM格式,以及如何将HOGDM转换为普通图格式。
- 普通图 (PG): 链接是边,表示两个节点之间的连接。
- 超图 (HG): 链接是超边,可以连接任意数量的节点。
- 单纯复形 (SC): 链接是超边或细胞,但每个超边连接的节点集合也必须形成超边。
- 细胞复形 (CC): 链接是细胞,细胞可以是零维的节点、一维的边、二维的面,等等。
- 普通图 (PG): 邻接由边完全确定,节点通过共享边连接。
- 超图 (HG): 邻接可以基于节点和超边的共享程度,例如基于超边的包含关系或基于节点和超边的边界关系。
- 单纯复形 (SC): 邻接基于边界关系,例如节点与其边界超边之间的关系。
- 细胞复形 (CC): 邻接基于边界关系,例如细胞与其边界细胞之间的关系。
- 超图 (Hypergraph, HG): 使用超边来表示多阶关系,可以建模各种复杂的图结构,例如社交网络中的群组、化学物质之间的相互作用等。
- 单纯复形 (Simplicial Complex, SC): 限制超图的定义,确保子集也形成超边,例如社交网络中的群组。
- 细胞复形 (Cell Complex, CC): 进一步扩展SC,允许形成更高维的子结构,例如分子中的环。
- 节点元组集合图 (Node-Tuple Collection Graph, NT-Col-Graph): 使用有序的节点元组来表示多阶关系,可以捕捉节点之间更复杂的关系。
- 子图集合图 (Subgraph Collection Graph, SCol-Graph): 使用子图集合来表示图中的结构信息,可以捕捉图中不同层次的结构信息。
- 子图元组集合图 (Subgraph-Tuple Collection Graph, ST-Col-Graph): 类似于SCol-Graph,但使用子图元组来表示更复杂的结构。
- 模式图 (Motif-Graph): 使用模式来定义邻接关系,例如三角形,可以捕捉图中的特定结构模式。
- 子图计数图 (Subgraph Count Graph, SCnt-Graph): 将子图数量作为附加信息,可以学习到更丰富的图结构信息。
- 嵌套图数据模型 (Nested Graph Data Model): 将子图或超图作为更高层次图中的节点,可以建模更复杂的图结构。
- 消息传递 (Message Passing, MP) 通道: HOGNN 架构的核心是 MP 机制,用于在图中的节点或实体之间交换信息。MP 通道的类型和连接方式决定了模型的学习能力和表达能力。
- 特征变换: 指定如何在不同 GNN 层之间转换特征向量。常见的特征变换方法包括非线性激活函数、归一化操作等。
- 提升和降低: 指定如何将输入的普通图转换为 HOGDM 格式,以及如何将 HOGDM 转换为普通图格式。提升和降低操作对于将 HOGNN 应用于实际任务至关重要。
- 基于超边邻域的 MP: 使用超边来定义 MP 通道,例如 Hypergraph Convolution 和 Hypergraph Attention。
- 基于边界邻域的 MP: 使用节点和超边之间的边界关系来定义 MP 通道,例如 HyperSAGE。
- 基于ego网络的 MP: 使用节点的 1-ego网络来定义 MP 通道,例如 Ego-GNN 和 GNN-AK。
- 基于重建的 MP: 通过删除节点或边来构建子图,并学习子图特征,例如 DropGNN 和 ReconstructionGNN。
- 基于通用子图邻域的 MP: 使用特定的子图集合来定义 MP 通道,例如 Subgraph Neural Networks。
- 基于模式邻域的 MP: 使用节点是否属于某个模式来定义 MP 通道,例如 HONE。
- 基于模式计数的 MP: 使用节点所属的模式的数量作为附加信息,例如 SCnt-Graph。
- 基于 motif 的 HOGNN: 使用 motif 来定义邻接关系,例如 MotifNet。
- 基于子图计数的 HOGNN: 使用子图的计数作为附加信息,例如 GSN。
- MP 通道的类型和连接方式: 选择合适的 MP 通道类型和连接方式对于提高模型的表达能力和预测精度至关重要。
- 特征变换方法: 选择合适的特征变换方法可以更好地捕捉图中的复杂关系。
- 提升和降低操作: 选择合适的提升和降低操作可以确保模型能够处理不同格式的图数据。
- 更高的表达能力: HOGNN 架构能够更有效地表示和处理图中的复杂结构,例如多阶关系、子图结构等,从而提高模型的表达能力。
- 更高的预测精度: HOGNN 架构能够学习到更丰富的图结构信息,从而提高模型的预测精度。
- 更强的鲁棒性: HOGNN 架构能够更好地抵抗噪声和异常值的影响。
- 同构性测试 (Graph Isomorphism Test): 检测两个图是否同构,即是否具有相同的结构和性质。HOGNN 的表达能力可以通过其能够区分的不同同构图的数量来衡量。
- 子图计数 (Substructure Counting): 计算图中特定子图的数量,例如三角形、环等。HOGNN 的表达能力可以通过其能够识别的子图类型的数量和精度来衡量。
- 函数逼近 (Function Approximation): 学习一个函数,能够逼近图中的特定性质,例如节点的度、边的权重等。HOGNN 的表达能力可以通过其能够逼近的函数类型的数量和精度来衡量。
- HOGDM 类型: 不同的 HOGDM 类型具有不同的表达能力。例如,超图可以表示更复杂的图结构,但可能需要更多的计算资源;单纯复形和细胞复形可以表示更丰富的子图结构,但可能需要更复杂的模型结构。
- MP 通道类型: 不同的 MP 通道类型具有不同的表达能力。例如,卷积操作可以有效地捕捉局部结构,但可能无法捕捉全局结构;注意力机制可以有效地捕捉长距离关系,但可能需要更多的计算资源。
- 特征变换方法: 不同的特征变换方法具有不同的表达能力。例如,ReLU 激活函数可以有效地引入非线性,但可能无法捕捉图中的复杂结构;余弦函数可以有效地捕捉节点之间的相似度,但可能需要更多的计算资源。
- 提升和降低操作: 不同的提升和降低操作会影响模型的表达能力。例如,简单的提升操作可能无法保留图中的所有结构信息;复杂的降低操作可能导致信息丢失。
- 更丰富的图结构信息: HOGNN 能够学习到比传统 GNN 更丰富的图结构信息,例如多阶关系、子图结构等,从而提高模型的表达能力。
- 更高的预测精度: HOGNN 能够学习到更丰富的图结构信息,从而提高模型的预测精度。
- 更强的泛化能力: HOGNN 能够学习到更丰富的图结构信息,从而提高模型的泛化能力。
- 计算复杂性: HOGNN 通常需要更多的计算资源,因为它们需要处理更复杂的图结构和更复杂的模型结构。
- 模型可解释性: HOGNN 的模型结构通常比较复杂,难以解释模型的决策过程。
- 数据预处理: HOGDM 的构建通常需要额外的数据预处理步骤,例如子图提取、模式识别等。
- 更复杂的图结构: 开发能够表示更复杂图结构的 HOGDM,例如包含循环、层次结构、异构图等。
- 更丰富的图属性: 开发能够表示更丰富图属性的 HOGDM,例如节点类型、边类型、图标签等。
- 更高效的图表示: 开发能够更高效地表示图数据的 HOGDM,例如压缩图表示、稀疏图表示等。
- 新的消息传递机制: 开发新的消息传递机制,例如基于注意力机制、基于随机化方法等。
- 新的特征变换方法: 开发新的特征变换方法,例如基于深度学习、基于图卷积等。
- 新的 HOGDM 与 HOGNN 的结合: 探索将新的 HOGDM 与现有的 HOGNN 模型相结合,例如将细胞复形与注意力机制相结合。
- 新的应用场景: 将 HOGNN 应用于更广泛的领域,例如时间序列分析、多模态学习、知识图谱等。
- 并行和分布式计算: 开发支持并行和分布式计算的 HOGNN 处理框架,例如使用 GPU、FPGA 等硬件加速。
- 内存计算: 探索内存计算技术在 HOGNN 中的应用,例如使用 Processing-In-Memory 技术。
- 图数据库集成: 将 HOGNN 集成到图数据库中,例如开发支持 HOGNN 查询语言的图数据库。
- 专用硬件加速器: 开发专用于 HOGNN 的硬件加速器,例如使用 FPGA 或 ASIC。
- 集成到现有硬件: 将 HOGNN 集成到现有的硬件中,例如使用 GPU 或 CPU。
- 减少通信开销: 开发支持全局公式的 HOGNN 模型,例如使用图卷积神经网络 (GCN) 的全局公式。
- 提高计算效率: 利用全局公式来提高 HOGNN 的计算效率。
- 结合时间信息: 将时间信息结合到 HOGNN 中,例如使用时间序列图或动态图。
- 预测时间相关事件: 使用 HOGNN 来预测时间序列图中的事件,例如股票价格、天气变化等。
- 利用 HOGNN 的层次计算模式: 利用 HOGNN 的层次计算模式来开发更有效的图压缩和摘要方法。
- 结合其他技术: 将 HOGNN 与其他技术相结合,例如图池化、图编码等。
- 增强 LLM 的结构推理能力: 使用 HOGNN 来增强 LLM 的结构推理能力,例如用于解决复杂逻辑推理问题。
- 开发新的 LLM 模型: 开发新的 LLM 模型,例如将 HOGNN 与 Transformer 模型相结合。



![[Linux内核驱动]自旋锁](http://pic.xiahunao.cn/[Linux内核驱动]自旋锁)















读写位深度24位的 bmp 文件)