什么是滑动窗口?
滑动窗口是算法中一种非常有用的技术,特别是在处理数据序列或数组时。它的核心思想是维护一个固定大小的窗口,这个窗口在数据序列上滑动,以便于在窗口内的元素上进行操作或计算。滑动窗口技术通常用于解决与数据子序列相关的问题,例如:
- 最大子数组和:找到数组中和最大的连续子数组。
- 最小覆盖子串:找到覆盖所有字符的最短子串。
- 最长不重复子串:找到最长的不包含重复字符的连续子串。
滑动窗口的基本操作:
- 初始化:设置窗口的起始和结束位置,通常起始位置
start和结束位置end都初始化为 0。 - 扩展窗口:将窗口的结束位置
end向右移动,即end++,以包含更多的元素。 - 收缩窗口:如果窗口的大小超出了限制,或者不再满足特定的条件(例如,需要保持窗口内元素的和不超过某个值),则将窗口的起始位置
start向右移动,即start++,以排除窗口左侧的元素。
滑动窗口的实现步骤:
- 初始化:设置窗口的起始和结束索引,以及可能需要的辅助数据结构(如哈希表、队列等)。
- 计算窗口值:根据问题需求,计算窗口内元素的和、最大值、最小值等。
- 滑动窗口:根据窗口内的条件,决定是扩展窗口还是收缩窗口。
- 如果窗口大小未达到要求,扩展窗口。
- 如果窗口大小达到要求但满足条件,记录结果,然后扩展窗口。
- 如果窗口大小达到要求但不满足条件,收缩窗口。
- 更新结果:在每次窗口滑动后,根据问题需求更新全局结果。
示例:最长不重复子串
假设我们要找到字符串中最长的不包含重复字符的子串。使用滑动窗口的方法,我们可以这样做:
- 使用一个哈希表来记录窗口内字符的出现次数。
- 使用两个指针表示窗口的起始和结束位置。
- 遍历字符串,将遇到的字符加入哈希表,并扩展窗口。
- 如果哈希表中字符的总数超过了窗口大小,说明有重复字符,需要收缩窗口。
- 在每次窗口滑动后,更新最长不重复子串的长度。
滑动窗口技术是一种非常灵活的方法,可以根据不同的算法问题进行调整和优化。
示例题目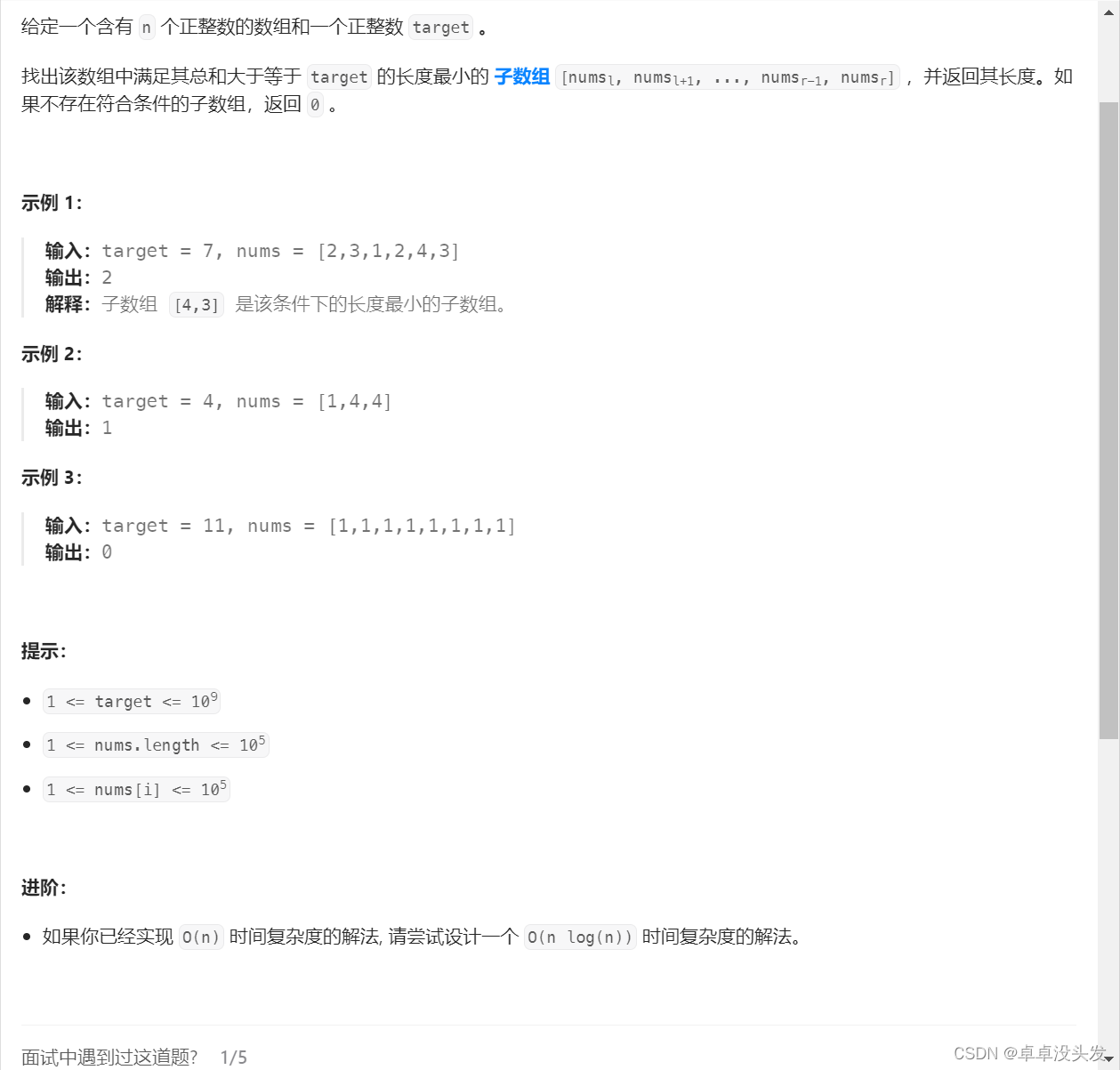
解题思路
这段代码是一个 JavaScript 函数,用于解决一个典型的滑动窗口问题:找到数组中和至少为 target 的最短子数组的长度。下面是这个函数的解题思路:
-
初始化变量:
start和end分别表示滑动窗口的起始和结束位置,初始时都设置为 0。len存储数组nums的长度。res用来存储最短子数组的长度,初始值设为Infinity,表示无穷大,因为我们要找到最短的长度。sum用来存储当前窗口内所有元素的和,初始值为 0。
-
外层循环:
- 使用
while循环,条件是end < len,确保end索引不会超出数组长度。
- 使用
-
扩展窗口:
- 在每次循环中,将
end索引对应的元素加到sum上,扩展窗口。
- 在每次循环中,将
-
检查窗口和:
- 使用内层
while循环检查当前窗口的和是否大于target。 - 如果
sum大于target,则需要收缩窗口。
- 使用内层
-
收缩窗口:
- 如果
sum大于target,则更新res为当前窗口长度end - start的最小值。 - 然后从
sum中减去start索引对应的元素,并将start向右移动一位,从而收缩窗口。
- 如果
-
更新结束索引:
- 无论是否收缩窗口,外层循环的每次迭代结束时,都将
end向右移动一位。
- 无论是否收缩窗口,外层循环的每次迭代结束时,都将
-
处理边界情况:
- 在循环结束后,如果
res仍然是Infinity,说明没有找到任何满足条件的子数组,此时返回 0。 - 如果找到了满足条件的子数组,返回
res的值。
- 在循环结束后,如果
-
返回结果:
- 使用三元运算符检查
res是否为Infinity,如果是,则返回 0;否则返回res。
- 使用三元运算符检查
这个函数的时间复杂度是 O(n),其中 n 是数组 nums 的长度,因为每个元素最多被访问两次(一次添加到 sum,一次从 sum 中减去)。空间复杂度是 O(1),因为我们只使用了固定数量的额外变量。
答案: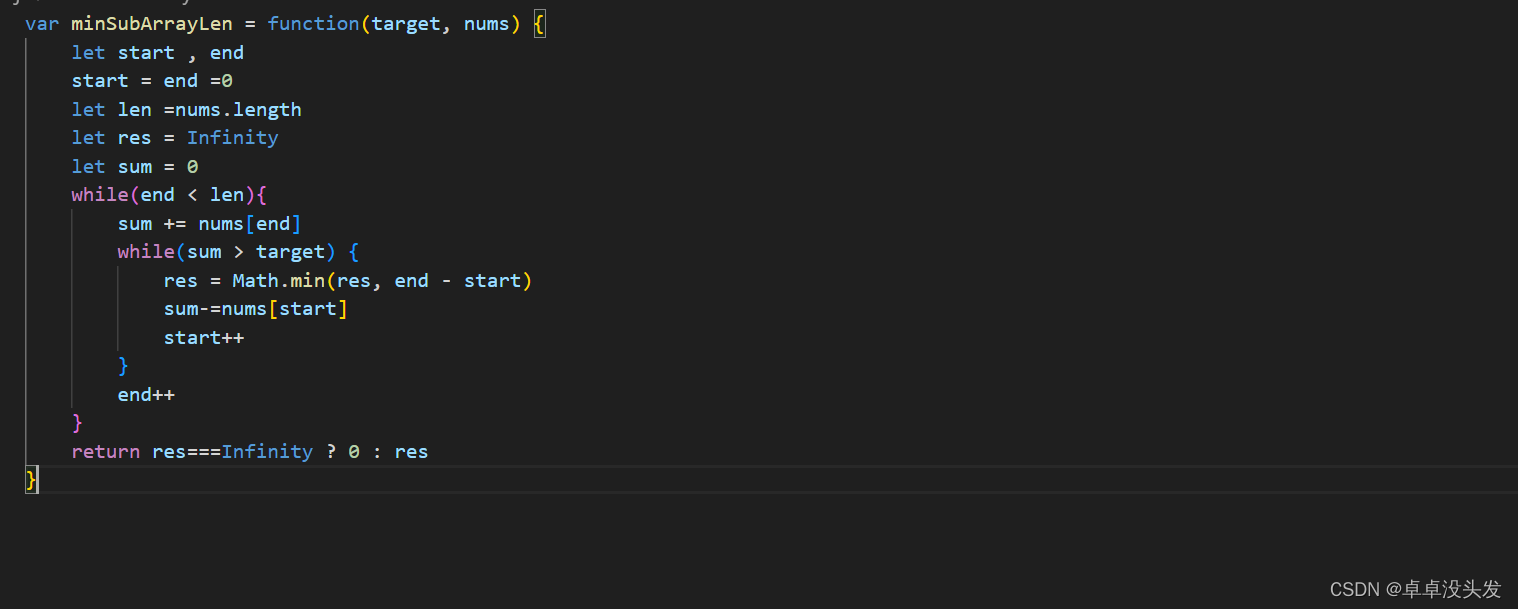
总结
滑动窗口是一种强大的算法工具,能够以线性时间解决多种子数组相关问题,是算法竞赛和工业界中常用的技术之一

安装)
)
)








)

)
底层转换原理,此篇带你理解清楚)



