目录
- 1.算法原理
- 2.数学模型
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
【智能算法】粒子群算法(PSO)原理及实现
配餐顺序: 采用混合粒子群算法 || 路径规划: 采用蚁群算法
2.数学模型
餐厅送餐多机器人多点配送路径规划,对模型进行以下假设:
- 单个机器人的配送量无法满足多个客人的需求量
- 多个机器人同时从取餐点出发,对所有所有客人进行配餐,配餐完结束后再次回到起始点
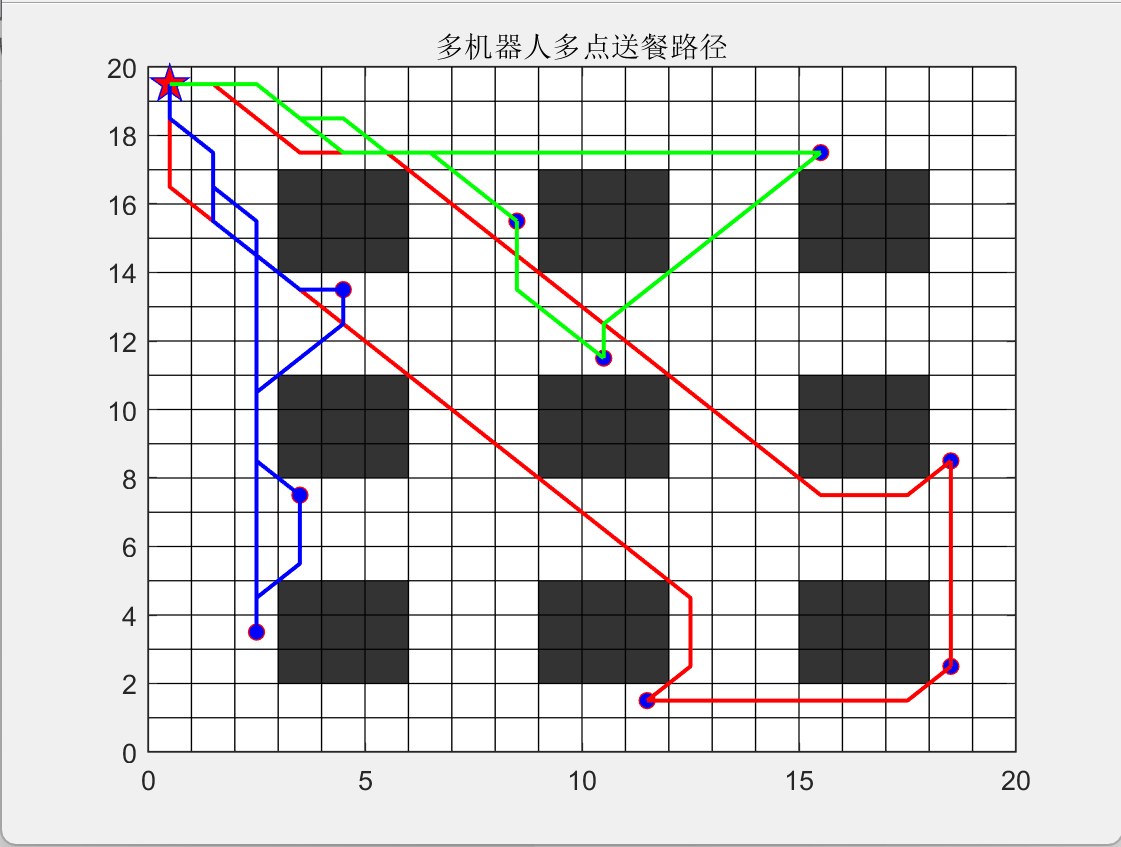
- 餐厅包含9张桌子和1个配餐点
🍀此模型为带容量限制的物流路径规划问题CVRP和机器人避障路径规划结合问题🍀
配餐顺序: 采用混合粒子群算法 || 路径规划: 采用蚁群算法

目标函数:
m i n Z = ∑ i = 0 n ∑ j = 0 , j ≠ i n ∑ k d i j x i j k (1) min Z=\sum_{i=0}^n\sum_{j=0,j\neq i}^n\sum_kd_{ij}x_{ijk}\tag{1} minZ=i=0∑nj=0,j=i∑nk∑dijxijk(1)
每个餐桌只能被访问一次:
∑ i = 0 n ∑ k x i j k = 1 ∀ j ∈ V , j ≠ 0 (2) \sum_{i=0}^n\sum_kx_{ijk}=1\quad\forall j\in V,j\neq0\tag{2} i=0∑nk∑xijk=1∀j∈V,j=0(2)
保证路径的连续性和回路的完整性:
∑ i = 0 , i ≠ j n x i j k = ∑ h = 0 , h ≠ j n x j h k ∀ j ∈ V , ∀ k (3) \sum_{i=0,i\neq j}^nx_{ijk}=\sum_{h=0,h\neq j}^nx_{jhk}\quad\forall j\in V,\forall k\tag{3} i=0,i=j∑nxijk=h=0,h=j∑nxjhk∀j∈V,∀k(3)
机器人容量限制:
∑ i = 0 n ∑ j = 0 , j ≠ i n q j x i j k ≤ Q ∀ k (4) \sum_{i=0}^n\sum_{j=0,j\neq i}^nq_jx_{ijk}\leq Q\quad\forall k\tag{4} i=0∑nj=0,j=i∑nqjxijk≤Q∀k(4)
每个餐桌的需求量被满足:
∑ i = 0 n ∑ k q j x i j k = q j ∀ j ∈ V (5) \sum_{i=0}^n\sum_kq_jx_{ijk}=q_j\quad\forall j\in V\tag{5} i=0∑nk∑qjxijk=qj∀j∈V(5)
路径的合法性(避免障碍物):
x i j k = 0 如果路径 ( i , j ) 不可行 (6) x_{ijk}=0\quad\text{如果路径 }(i,j)\text{ 不可行}\tag{6} xijk=0如果路径 (i,j) 不可行(6)
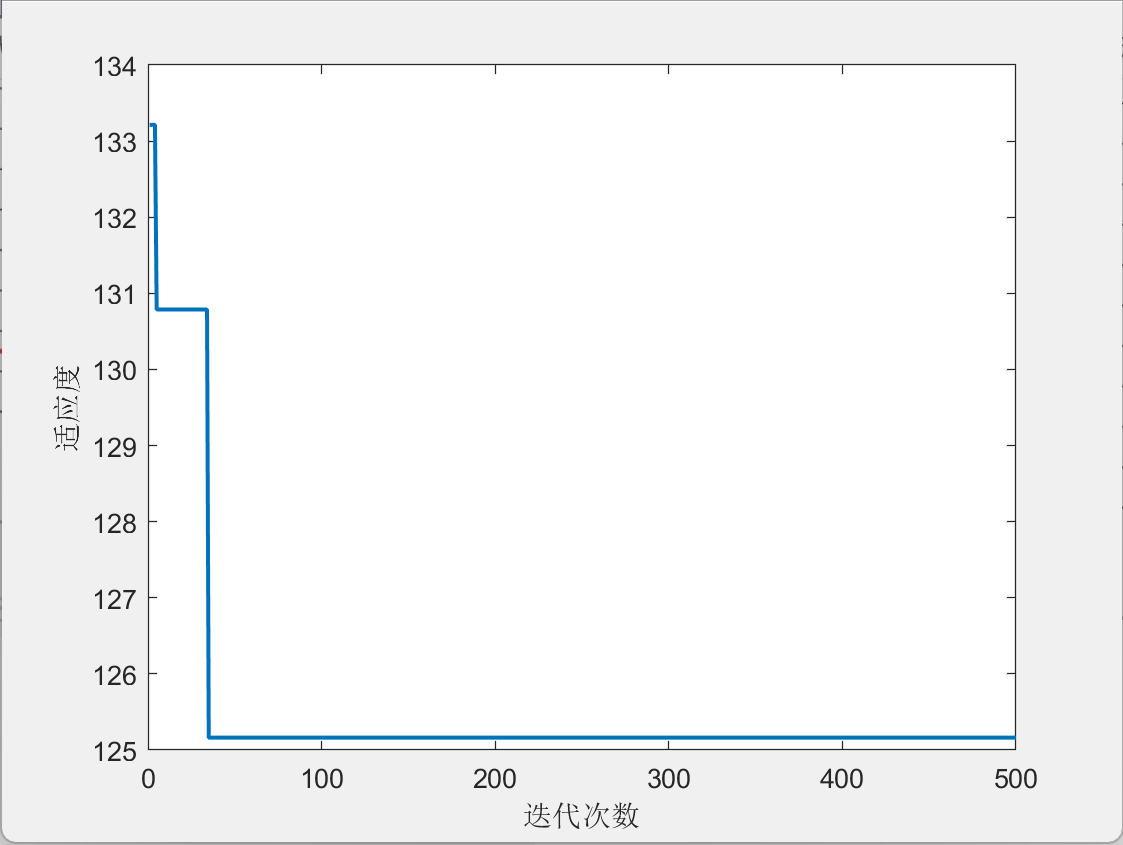
3.结果展示
4.参考文献
[1] 蔡军,钟志远.改进蚁群算法的送餐机器人路径规划[J].智能系统学报,2024,19(02):370-380.
[2] 汪繁荣,杜力,徐光辉.基于改进蚁群算法的分布式多机器人协同路径规划[J].中南民族大学学报(自然科学版),2023,42(05):650-657.


:deepstream-app源码详解(03)解析配置文件)
解决方法)



)
从入门到精通系列之十九:Operator模式)






)



