小波变换具有良好的时频局部化特性和多分辨率特性，可准确定位信号的突变点并可在不同尺度上描述信号的局部细节特征，被广泛应用于信号降噪。但标准正交小波变换不具有平移不变性，采用标准正交小波对信号消噪后，会在脉冲尖峰处产生Gibbs振荡现象，造成脉冲信号的失真。

非下采样小波NSW具有平移不变性，用于信号消噪可以较好地抑制Gibbs振荡现象。但NSW变换只对信号的低频部分进行分解，对信号的高频部分不再进行剖分，导致分解后信号高频部分的频率分辨率较差。这对于主要信息包含在低频部分的信号比较适合，但对于强噪声背景下的信号并不适用。因为很多信号中的脉冲尖峰和剧烈振荡部分等重要信息主要位于高频部分，分解后和噪声混杂在一起，不对高频部分进行再次剖分提高其频率分辨率，去噪时就无法有效区分有用细节信息和噪声，会导致较多的有用细节信息被误删除且部分噪声被误保留，从而破坏脉冲累积轮廓的几何特征。非下采样小波包NWP分解可较好地克服这一缺点，它在对信号的低频部分进行分解的同时，对小波变换中没有分解的高频部分也进行进一步的分解，使得高频频带被分解的更加细致，可为信号消噪提供更加丰富和详细的信息，对于含较强噪声的低信噪比信号可取的更好的消噪效果。

鉴于此，采用非下采样小波包分析进行滚动轴承故障诊断，运行环境为MATLAB R2021B。

非下采样小波包时频谱如下：

3层小波包分解及小波包时频谱图：

8个子频带波形：

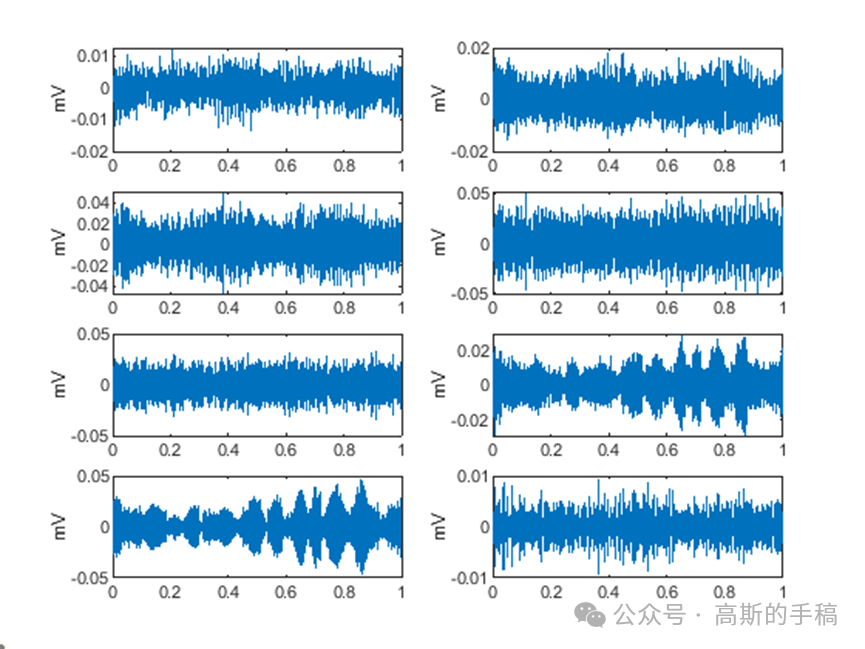
8个子带对应的包络谱：

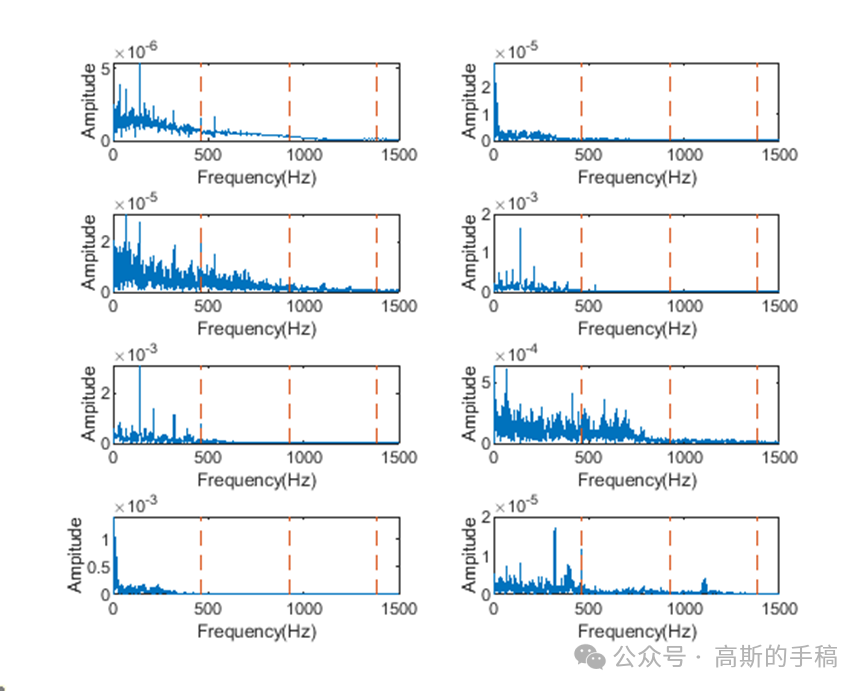
可见第3个子带和第8个子带的包络谱故障特征频率较为明显，不妨重新看一下：

switch numcase {1,'blocks'}       % blocks.tt = linspace(0,1,len);  x = zeros(1,len);for j=1:11x = x + ( h(j)*(1+sign(tt-t(j)))/2 );end完整代码：mbd.pub/o/bread/YpyXk5Zrcase {2,'bumps'}        % bumps.h  = abs(h);w  = 0.01*[0.5 0.5 0.6 1 1 3 1 1 0.5 0.8 0.5];tt = linspace(0,1,len);  x = zeros(1,len);for j=1:11x = x + ( h(j) ./ (1+ ((tt-t(j))/w(j)).^4));end

工学博士，担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家，擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。