摘要

尽管线性模型很简单，但它在时间序列预测中表现良好，即使是在与更深入、更昂贵的模型竞争时也是如此。已经提出了许多线性模型的变体，通常包括某种形式的特征归一化，以提高模型的泛化。本文分析了用这些线性模型体系结构可表示的函数集。通过这样做，我们证明了时间序列预测的几种流行的线性模型变体是等效的，并且在功能上与标准的无约束线性回归难以区分。 我们描述了每个线性变量的模型类。我们证明了每个模型都可以被重新解释为在适当增强的特征集上的无约束线性回归，因此在使用均方损失函数时承认封闭形式的解决方案。我们提供的实验证据表明，在检查模型学习几乎相同的解决方案，并最终证明，更简单的封闭形式的解决方案是优越的预测在72%的测试设置。

线性模型定义:令x∈rl是一个上下文向量。DLinear的工作原理是把x分解成“趋势”和“季节”分量。趋势分量是通过对x的分量取一个移动平均值来定义的。季节分量由残差$x_{seasonal}:=x-x_{trend}$给出。移动平均线被填充，这样它就保留了x的维度。然后，我们把x -季节性和x -季节性分开，把它们传递给单独的可学习的线性层。

在本文中，我们深入研究了几个著名的线性时间序列预测模型的数学。我们充分描述了使用每个架构可表达的功能集。我们显示，有些引人注目的是，它们本质上都是等效的:对应于无约束或弱约束(通过特征增强)线性回归。最小二乘线性回归的凸性表明，这些模型的行为实际上应该是难以区分的。我们提供了支持这一假设的实验证据，表明在实践中，所有模型都趋向于相同的最优。此外，我们证明了最小二乘线性回归的封闭形式解的性能与梯度下降训练的解相当或更好。我们的贡献是:

• 数学证明，几种流行的线性时间序列预测模型本质上是相同的。
• 实验证据表明，当对相同的数据进行训练时，每个模型确实倾向于相同的解决方案，只是偏差参数不同。
• 定量证据表明，封闭形式的普通最小二乘(OLS)解决方案通常优于使用随机梯度下降训练的现有模型。

为了本文的目的，我们将“模型类”称为由模型体系结构引起的函数的参数集。例如，一个没有隐藏层的单层线性神经网络的模型类为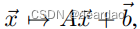
其中a和b的维数是合适的。在本文的剩余部分，我们称之为“线性”。在本节中，我们用线性模型定义预测任务。然后，我们分析了广泛使用的DLinear(第3.1.1节)和最近的SoTA FITS架构(第3.1.2节)。我们从数学上证明了这些模型与线性回归是等价的，因为它们具有相同的模型类。然后，我们在第3.2节中定义和讨论了用于时间序列预测的几种可逆数据归一化策略。这些归一化策略产生额外的线性模型变体，即RLinear、NLinear和FITS+IN
(如Xu等人所说，即FITS与实例规范化。