
📃博客主页: 小镇敲码人
💚代码仓库,欢迎访问
🚀 欢迎关注:👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨,我自踏雪寻梅香。 万千浮云遮碧月,独傲天下百坚强。 男儿应有龙腾志,盖世一意转洪荒。 莫使此生无痕度,终归人间一捧黄。🍎🍎🍎
❤️ 什么?你问我答案,少年你看,下一个十年又来了 💞 💞 💞

【ZZULI数据结构实验四】:C语言排序算法大比拼
- 🪡 实验的内容和要求
- 🪡 结构设计及函数接口
- 🪡 排序函数的具体实现
- 🚵🏻♀️ 冒泡排序的实现
- 🚵🏻♀️ 选择排序的实现
- 🚵🏻♀️ 直接插入排序的实现
- 🚵🏻♀️ 折半插入排序的实现
- 🍟 OJ测试
- 🚵🏻♀️ 希尔排序
- 🚵🏻♀️ 堆排序
- 🚵🏻♀️ 快速排序
- 🍟 递归版本
- 🍟 非递归版本
- 🪡 测试及结果演示
- 🚵🏻♀️ 菜单函数
- 🚵🏻♀️ 正确性测试及中间结果打印
- 🚵🏻♀️ 稳定性测试
- 🚵🏻♀️ 性能测试
前言:本篇博客不讲具体的排序算法原理,如果你对某个排序算法的原理不太理解,请看博主这篇博客八大排序C语言实现,以下排序的代码的正确性都在上篇博客八大排序中进行过OJ测试,不做100%保证,但是大概率应该是没什么问题,如有问题,敬请斧正。
🪡 实验的内容和要求

🪡 结构设计及函数接口
实验要求里面要求我们判断排序的算法稳定性,我们需要保存初始时每个数据对应的下标,即把数据和初始时的下标用结构体绑在一起,这里具体的原理我们等会再解释:
typedef int DataType;
typedef struct DataNode
{DataType data_;//数据的值int idx;//数组开始时的下标}Node;
各种函数接口:
// 交换函数
void Swap(Node* a, int* b);
//打印数组
void PrintArr(Node* a, int n);
// 直接插入排序
void InsertSort(Node* a, int n);//折半插入排序
void BinInsertSort(Node* a, int n);// 希尔排序
void ShellSort(Node* a, int n);// 选择排序
void SelectSort(Node* a, int n);// 堆排序
void AdjustDown(Node* a, int n, int root);
void HeapSort(Node* a, int n);// 冒泡排序
void BubbleSort(Node* a, int n);// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(Node* a, int left, int right,int n);void QuickSort(Node* a, int left, int right,int n);//快速排序递归实现
// 快速排序 非递归实现
void QuickSortNonR(Node* a, int left, int right,int n);bool is_stable(Node* a, int n);//判断某个排序算法是否是稳定的🪡 排序函数的具体实现
🚵🏻♀️ 冒泡排序的实现
// 冒泡排序
void BubbleSort(Node* a, int n)
{int flag = 0;//设置标志变量优化int cnt = 0;for (int i = 0; i < n - 1; i++)//排序n个数,需要n-1趟{flag = 0;for (int j = 0; j < n - i - 1; j++){if (a[j].data_ > a[j + 1].data_)//如果满足交换条件交换{cnt++;flag = 1;//如果存在交换,将flag设置为1Swap(&a[j], &a[j + 1]);}}//printf("第%d躺排序结果:", i);//PrintArr(a, n);if (flag == 0)//如果这一趟没有数交换说明已经有序,结束排序{break;}}printf("BubbleSort:\n");printf("比较和交换的次数为:%d\n", cnt);
}
🚵🏻♀️ 选择排序的实现
// 选择排序
void SelectSort(Node* a, int n)
{int k = 0;int j = 0;int mini = 0;//创建变量,保存当前最小值的下标int cnt = 0;int cnt1 = 0;for (int i = 0; i < n - 1; i++)//n-1趟就排完了{mini = i;for (j = i; j < n; j++){if (a[mini].data_ > a[j].data_)//找出目前最小的元素下标{cnt++;mini = j;}}if (mini != i)//如果这个下标不是i位置,就交换{Swap(&a[mini], &a[i]);cnt1++;}//printf("第%d躺排序结果:", k++);//PrintArr(a, n);}printf("SelectSort:\n");printf("比较的次数为: %d\n", cnt);printf("交换的次数为: %d\n", cnt1);
}
🚵🏻♀️ 直接插入排序的实现
// 插入排序
void InsertSort(Node* a, int n)
{//0~end有序int end = 0;int i = 0;int cnt = 0;int cnt1 = 0;while (end < n - 1){Node tmp = a[end + 1];//插入位置的元素for (i = end; i >= 0; i--)//调整其到正确位置,将大于tmp的都往整体后挪动一位,然后插入tmp{if (a[i].data_ > tmp.data_){cnt++;cnt1++;a[i + 1] = a[i];}else{cnt++;break;}}cnt1++;a[i + 1] = tmp;end++;//printf("第%d躺排序结果:", end);//PrintArr(a, n);}printf("InsertSort:\n");printf("比较的次数为: %d\n", cnt);printf("挪动数据次数为: %d\n", cnt1);
}🚵🏻♀️ 折半插入排序的实现
这里对这个之前没有阐述过的排序的原理做一下阐述:折半插入排序算法是对直接插入排序的一个小优化,它加入了二分算法(也叫折半查找算法),可以快速的找出我们每一次需要插入的位置( l o g N logN logN的量级),但是挪动数据部分的时间效率和直接插入排序一样,所以整体性能提升不大,还 O ( N 2 ) O(N^2) O(N2)的量级。
代码实现:
//折半插入排序
void BinInsertSort(Node* a, int n)
{//0~end有序int end = 0;int i = 0;int cnt = 0;int cnt1 = 0;while (end < n - 1){Node tmp = a[end + 1];//插入位置的元素//开始二分查找int left = 0, right = end;int pos = end+1;//保存满足要求的下标while (left <= right){int mid = left + ((right - left) >> 2);if (a[mid].data_ <= tmp.data_){cnt++;left = mid + 1;}else if(a[mid].data_ > tmp.data_){cnt++;pos = mid;right = mid - 1;}}//把pos位置及其之后的数据往后挪一位for (int i = end; i >= pos; --i){cnt1++;a[i + 1] = a[i];}cnt1++;a[pos] = tmp;end++;//printf("第%d躺排序结果:", end);//PrintArr(a, n);}printf(" BinInsertSort:\n");printf("比较的次数为: %d\n", cnt);printf("挪动数据次数为: %d\n", cnt1);
}
🍟 OJ测试
之前没有对这个代码的正确性做过测试,现在我们借助这个OJ题来测试一下:
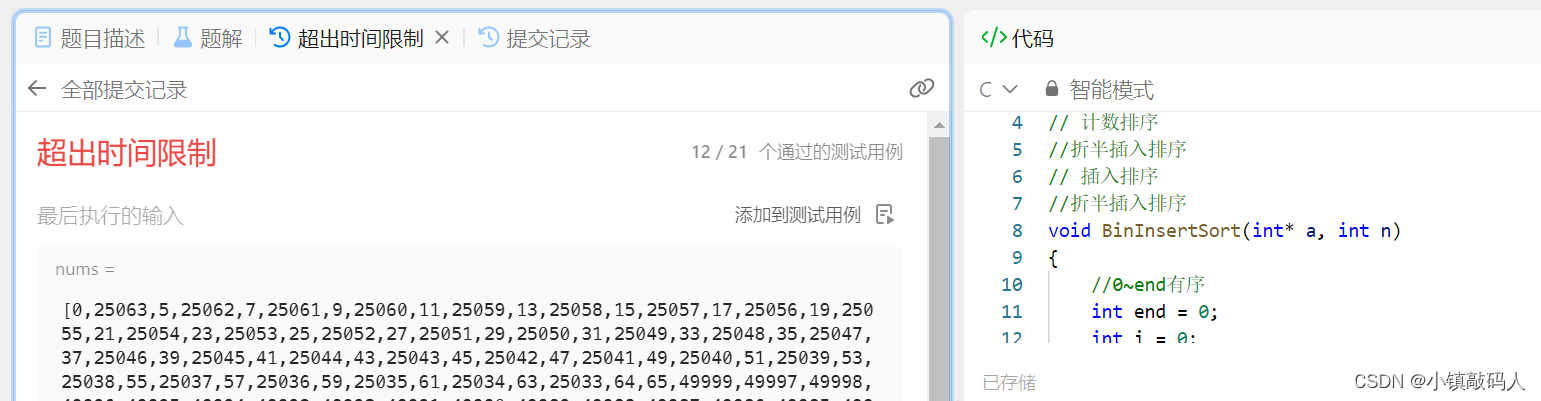
可以看到卡到了第12个数据,直接插入排序的测试情况和它一致,所以效率上并没有太大提升,注意要把Node类型改为int。可以基本认为我们的折半排序算法是正确的。
🚵🏻♀️ 希尔排序
// 希尔排序
void ShellSort(Node* a, int n)
{int gap = n;//令gap等于nint i = 0;//i为控制每次插入排序的开始的位置的变量int j = 0;//j为每次直接插入排序的变量int cnt = 0;int cnt1 = 0;int k = 0;while (gap > 1){gap = gap / 3 + 1;//gap不为一个固定的值,预处理多次,让我们的分组插入的效果更加好,降低后面直接插入的时间for (i = 0; i < n - gap; i++)//gap为某一个值时的分组插入,这里我们使用多组同时走插入排序{int end = i;Node tmp = a[end + gap];for (j = end; j >= 0; j -= gap){if (tmp.data_ < a[j].data_)//小于就把大的值往后移{cnt++;cnt1++;a[j + gap] = a[j];}else//找到了,break{cnt++;break;}}cnt1++;a[j + gap] = tmp;//将tmp赋值给正确位置}//printf("第%d躺排序结果:",k++);//PrintArr(a, n);}printf("ShellSort:\n");printf("比较的次数为: %d\n", cnt);printf("挪动数据次数为: %d\n", cnt1);
}
🚵🏻♀️ 堆排序
// 向下调整
void AdjustDown(Node* a, int n, int root,int* cnt,int* cnt1)
{int child = root * 2 + 1;while (child < n){if (child + 1 < n && a[child].data_ < a[child + 1].data_)//找出最大的孩子{(*cnt)++;child = child + 1;}if (a[root].data_ < a[child].data_)//如果根节点的值比最大的孩子小就交换{(*cnt)++;(*cnt1)++;Swap(&a[root], &a[child]);root = child;child = root * 2 + 1;}else//否则调整完成{cnt++;break;}}
}
//堆排序,大堆,排升序
void HeapSort(Node* a, int n)
{assert(a);int cnt = 0;int cnt1 = 0;for (int i = (n - 1 - 1) / 2; i >= 0; i--)//我们向上调整,原地建一个大堆{AdjustDown(a, n, i,&cnt,&cnt1);}int i = 0;//将大堆最大的和最后一个元素交换,并向下调整for (int end = n - 1; end >= 0; --end){cnt1++;Swap(&a[0], &a[end]);//将堆顶元素放到堆最后面去AdjustDown(a, end, 0,&cnt,&cnt1);//此时的end就代表我们的元素个数//printf("第%d躺排序结果:", i++);//PrintArr(a,n);}printf("HeapSort:\n");printf("比较的次数为: %d\n", cnt);printf("交换的次数为: %d\n", cnt1);
}
🚵🏻♀️ 快速排序
🍟 递归版本
// 快速排序递归实现
// 快速排序hoare版本
int get_mid(Node* a, int left, int right)
{int mid = (left + right) / 2;//中间下标的数if (a[left].data_ < a[mid].data_)//如果left位置的值小于mid位置的值{if (a[mid].data_ < a[right].data_)//如果right位置的值大于mid位置的值,那么mid位置的值就是第2大的(中位数){return mid;}else if (a[left].data_ > a[right].data_)//left位置的值大于right位置的值,mid是最大的{return left;}elsereturn right;}else//a[left] >= a[mid]{if (a[mid].data_ > a[right].data_)//mid位置的值大于right位置的值return mid;else if (a[left].data_ < a[right].data_)//left不是最大的return left;elsereturn right;}
}int k = 0;
int PartSort1(Node* a, int left, int right,int n)
{int mid = get_mid(a, left, right);//三数取中找中位数Swap(&a[mid], &a[left]);//交换int keyi = left;//记录关键元素的位置,方便最后的交换while (left < right)//如果left < right就退出循环{while (left < right && a[right].data_ >= a[keyi].data_)//先找小(严格找小),也要加上left < right的条件,防止越界 {right--;}while (left < right && a[left].data_ <= a[keyi].data_)//再找大(严格找大),同样的越界条件要加上{left++;}Swap(&a[left], &a[right]);//找到了交换}Swap(&a[keyi], &a[left]);//最后交换keyi元素和最后一个小的元素的位置,这样单趟就排完了,keyi位置的元素到了正确位置,不用管它了//printf("第%d躺排序结果:",k++);//PrintArr(a,n);return left;
}void QuickSort(Node* a, int left, int right,int n)
{if (left >= right)//一个元素或者区间不存在的情况递归就结束return;int i = 0;int mid = PartSort1(a, left, right,n);//[left,mid-1] mid [mid+1,right]QuickSort(a, left, mid - 1,n);//继续递归左边,执行相同的单趟排序的思路QuickSort(a, mid + 1, right,n);//继续递归右边,执行相同的单趟排序的思路
}
🍟 非递归版本
非递归版本需要栈来辅助,代码已经放在文章开头。
int k = 0;
int PartSort1(Node* a, int left, int right,int n)
{int mid = get_mid(a, left, right);//三数取中找中位数Swap(&a[mid], &a[left]);//交换int keyi = left;//记录关键元素的位置,方便最后的交换while (left < right)//如果left < right就退出循环{while (left < right && a[right].data_ >= a[keyi].data_)//先找小(严格找小),也要加上left < right的条件,防止越界 {right--;}while (left < right && a[left].data_ <= a[keyi].data_)//再找大(严格找大),同样的越界条件要加上{left++;}Swap(&a[left], &a[right]);//找到了交换}Swap(&a[keyi], &a[left]);//最后交换keyi元素和最后一个小的元素的位置,这样单趟就排完了,keyi位置的元素到了正确位置,不用管它了//printf("第%d躺排序结果:",k++);//PrintArr(a,n);return left;
}// 快速排序 非递归实现
void QuickSortNonR(Node* a, int left, int right,int n)
{Stack ps;//创建栈对象StackInit(&ps);//初始化栈对象StackPush(&ps, right);//入根节点的区间值,先入右,再入左,这样我们拿的时候就可以先拿到左StackPush(&ps, left);while (!StackEmpty(&ps))//如果栈为空,排序完成{int left1 = StackTop(&ps);//拿到栈顶区间的左边边界StackPop(&ps);//pop掉左边边界int right1 = StackTop(&ps);//拿到栈顶区间的左边边界StackPop(&ps);//pop掉右边边界int mid = PartSort1(a, left1, right1,n);//走一趟快速排序,哪个版本都可以,这里我们用的前后指针if (right1 > mid + 1)//先入右边区间,如果右边区间存在且长度不为1的话{StackPush(&ps, right1);StackPush(&ps, mid + 1);}if (left1 < mid - 1)//再入左边区间,如果左边区间存在且长度不为1的话{StackPush(&ps, mid - 1);StackPush(&ps, left1);}}StackDestroy(&ps);//销毁栈
}
🪡 测试及结果演示
注意:由于快速排序递归版本需要从外面传一个变量(使用指针)进来才便于统计比较和交换的次数,所以只有这个排序我们没有打印比较和交换次数,如果你不嫌麻烦,在外面的接口打印也是可以的。
🚵🏻♀️ 菜单函数
#include"sort.h"void Test1()
{printf("请输入要测试的数据的个数: \n");int n = 0;scanf("%d", &n);Node* a = (Node*)malloc(sizeof(Node) * n);Node* tmp = (Node*)malloc(sizeof(Node) * n);printf("请输入要测试的数据: \n");for (int i = 0; i < n; ++i){scanf("%d", &a[i].data_);a[i].idx = i;}printf("请输入你想测试的排序:\n");while (1){printf("****************************************************************\n");printf("**********************1.BubbleSort *****************************\n");printf("**********************2.InsertSort *****************************\n");printf("**********************3.BinInsertSort **************************\n");printf("**********************4.ShellSort*******************************\n");printf("**********************5.SelectSort******************************\n");printf("**********************6.HeapSort********************************\n");printf("**********************7.QuickSort ******************************\n");printf("**********************8.QuickSortNonR **************************\n");printf("**********************9.return **************************\n");printf("****************************************************************\n");int b = 0;scanf("%d", &b);switch (b){case 1: {memcpy(tmp,a,sizeof(Node)* n); BubbleSort(tmp, n);}break;case 2: {memcpy(tmp, a, sizeof(Node) * n);InsertSort(tmp, n); }break;case 3: {memcpy(tmp, a, sizeof(Node) * n);BinInsertSort(tmp, n); }break;case 4: {memcpy(tmp, a, sizeof(Node) * n);ShellSort(tmp, n); }break;case 5: {memcpy(tmp, a, sizeof(Node) * n);SelectSort(tmp, n); }break;case 6: {memcpy(tmp, a, sizeof(Node) * n);HeapSort(tmp, n); }break;case 7: {memcpy(tmp, a, sizeof(Node) * n);QuickSort(tmp,0,n-1,n); }break;case 8: {memcpy(tmp, a, sizeof(Node) * n);QuickSortNonR(tmp,0,n-1,n);}break;case 9: return;break;default:printf("输入错误,请重新输入\n");break;}}
}void Test2()
{srand(time(NULL));int N = 100000;printf("N: %d\n", N);Node* a1 = (Node*)malloc(sizeof(Node) * N);if (a1 == NULL){printf("a1 malloc failed\n");exit(-1);}Node* a2 = (Node*)malloc(sizeof(Node) * N);if (a2 == NULL){printf("a2 malloc failed\n");exit(-1);}Node* a3 = (Node*)malloc(sizeof(Node) * N);if (a3 == NULL){printf("a3 malloc failed\n");exit(-1);}Node* a4 = (Node*)malloc(sizeof(Node) * N);if (a4 == NULL){printf("a4 malloc failed\n");exit(-1);}Node* a5 = (Node*)malloc(sizeof(Node) * N);if (a5 == NULL){printf("a5 malloc failed\n");exit(-1);}Node* a6 = (Node*)malloc(sizeof(Node) * N);if (a6 == NULL){printf("a6 malloc failed\n");exit(-1);}Node* a7 = (Node*)malloc(sizeof(Node) * N);if (a7 == NULL){printf("a7 malloc failed\n");exit(-1);}Node* a8 = (Node*)malloc(sizeof(Node) * N);if (a8 == NULL){printf("a8 malloc failed\n");exit(-1);}for (int i = 0; i < N; ++i){a1[i].data_ = rand() % N+i;a1[i].idx = i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}InsertSort(a1,N);bool flag1 = is_stable(a1,N);BinInsertSort(a2, N);bool flag2 = is_stable(a2,N);BubbleSort(a3,N);bool flag3 = is_stable(a3,N);SelectSort(a4, N);bool flag4 = is_stable(a4,N);ShellSort(a5, N);bool flag5 = is_stable(a5,N);QuickSort(a6, 0, N - 1, N);bool flag6 = is_stable(a6,N);HeapSort(a7, N);bool flag7 = is_stable(a7,N);QuickSortNonR(a8, 0, N - 1, N);bool flag8 = is_stable(a8, N);printf("InsertSort stability:\n");if (flag1)printf("Yes\n");elseprintf("No\n");printf("BinInsertSort stability:\n");if (flag2)printf("Yes\n");elseprintf("No\n");printf("BubbleSort stability:\n");if (flag3)printf("Yes\n");elseprintf("No\n");printf("SelectSort stability:\n");if (flag4)printf("Yes\n");elseprintf("No\n");printf("ShellSort stability:\n");if (flag5)printf("Yes\n");elseprintf("No\n");printf("QuickSort stability:\n");if (flag6)printf("Yes\n");elseprintf("No\n");printf("HeapSort stability:\n");if (flag7)printf("Yes\n");elseprintf("No\n");printf("QuickSortNonR stability:\n");if (flag8)printf("Yes\n");elseprintf("No\n");
}void Test3()
{srand(time(NULL));int N = 100000;printf("N: %d\n", N);Node* a1 = (Node*)malloc(sizeof(Node) * N);if (a1 == NULL){printf("a1 malloc failed\n");exit(-1);}Node* a2 = (Node*)malloc(sizeof(Node) * N);if (a2 == NULL){printf("a2 malloc failed\n");exit(-1);}Node* a3 = (Node*)malloc(sizeof(Node) * N);if (a3 == NULL){printf("a3 malloc failed\n");exit(-1);}Node* a4 = (Node*)malloc(sizeof(Node) * N);if (a4 == NULL){printf("a4 malloc failed\n");exit(-1);}Node* a5 = (Node*)malloc(sizeof(Node) * N);if (a5 == NULL){printf("a5 malloc failed\n");exit(-1);}Node* a6 = (Node*)malloc(sizeof(Node) * N);if (a6 == NULL){printf("a6 malloc failed\n");exit(-1);}Node* a7 = (Node*)malloc(sizeof(Node) * N);if (a7 == NULL){printf("a7 malloc failed\n");exit(-1);}Node* a8 = (Node*)malloc(sizeof(Node) * N);if (a8 == NULL){printf("a8 malloc failed\n");exit(-1);}for (int i = 0; i < N; ++i){a1[i].data_ = rand() % N;a1[i].idx = i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}int begin1 = clock();BubbleSort(a1, N);int end1 = clock();int begin2 = clock();SelectSort(a2, N);int end2 = clock();int begin3 = clock();InsertSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1,N);//三路划分版本int end5 = clock();int begin6 = clock();ShellSort(a6, N);int end6 = clock();int begin7 = clock();BinInsertSort(a7, N);int end7 = clock();int begin8 = clock();QuickSortNonR(a8,0,N-1,N);int end8 = clock();printf("BubbleSort:%dms\n", end1 - begin1);printf("SelectSort:%dms\n", end2 - begin2);printf("InsertSort:%dms\n", end3 - begin3);printf("HeapSort:%dms\n", end4 - begin4);printf("QuickSort :%dms\n", end5 - begin5);printf("ShellSort:%dms\n", end6 - begin6);printf("BinInsertSort:%dms\n", end7 - begin7);printf("QuickSortNonR:%dms\n", end8 - begin8);}
void menu()
{printf("请输入你要测试的排序项目:\n");while (1){printf("**********************************************************\n");printf("**********************1.正确性测试************************\n");printf("**********************2.稳定性测试************************\n");printf("**********************3.性能测试**************************\n");printf("**********************4.退出程序**************************\n");printf("**********************************************************\n");int a = 0;scanf("%d", &a);switch(a){case 1: Test1();break;case 2: Test2();break;case 3: Test3();break;case 4: exit(-1);break;default:printf("输入错误,请重新输入\n");break;}}
}
int main()
{menu();return 0;
}
🚵🏻♀️ 正确性测试及中间结果打印
其实正确性的测试我们已经使用OJ题测试过了,这里再做一次是为了迎合实验的需要,数据量较小的时候,可以把打印中间结果的注释拿掉,但是等会测试性能和排序算法稳定性时一定要记得把这个给注释掉,因为IO打印是很耗时间的,不知道要等到什么时候去。
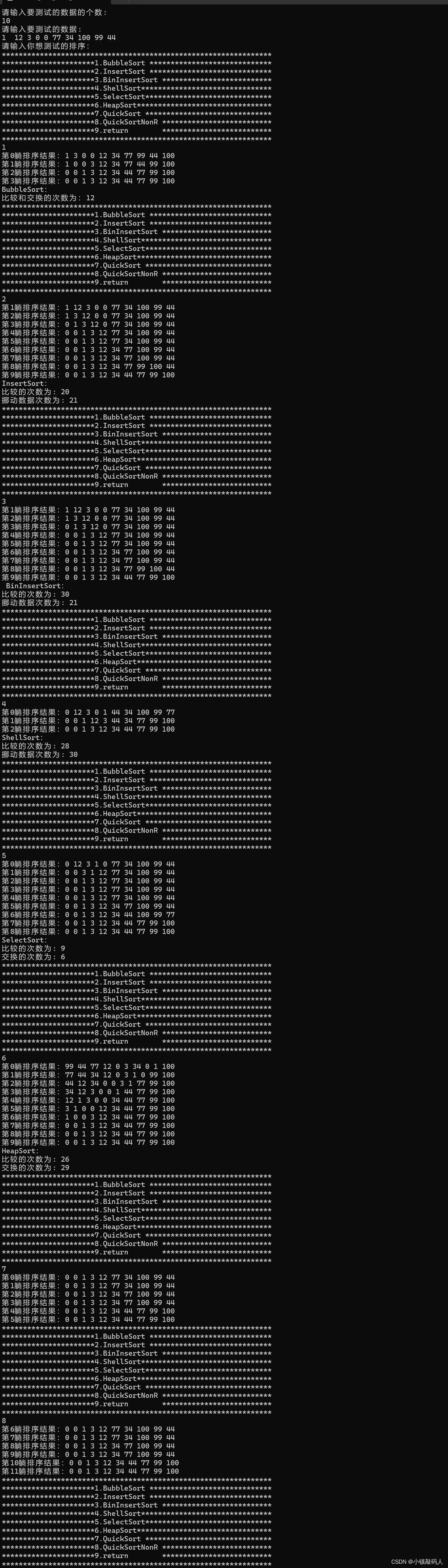
数据:第一行是数组的个数,第二行是数据。
10
1 12 3 0 0 77 34 100 99 44
测试结果:
🚵🏻♀️ 稳定性测试
稳定性测试函数:
bool is_stable(Node* a, int n)
{for (int i = 0; i < n; ++i){for (int j = i + 1; j < n; ++j){if (a[i].data_ == a[j].data_ && a[i].idx > a[j].idx)return false;}}return true;
}
稳定性测试的原理是:先使用结构体保存数组开始的值对应的下标,然后排序之后,看相等的值之间的先后顺序有没有发生变化,从0下标开始,去找它后面相等的值,如果这个值的初始下标在它的前面,说明这个排序算法就是不稳定的。
稳定性测试的结果:(我们造了10w个数据,这么大的数据量足以说明真相,而且我们的值是随机值,因为随机值函数只能生成3w多个,所以我们给它的后面+i,尽量减少重复)
注意:要把打印中间结果代码的注释掉,可能会有些算法的交换或者比较次数变成负数,这是正常的,因为int的返回最大只有2^31-1, O ( N 2 ) O ( N^2 ) O(N2) 的算法数据量一大,是完全可能超过这个范围的,溢出了自然就变成负数了,我们不用管。
10w个数据测试:
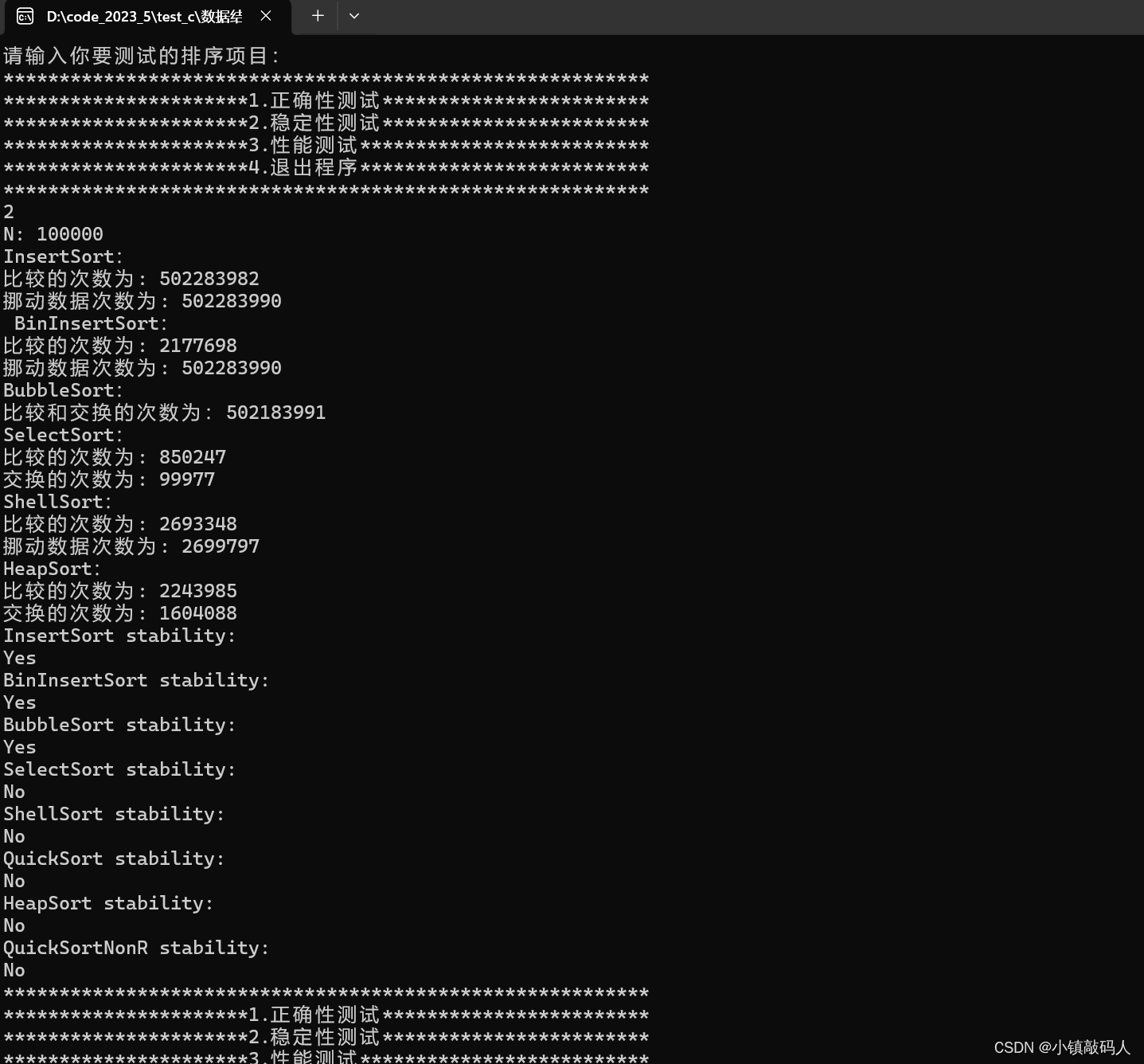
与预期结果一致。
🚵🏻♀️ 性能测试
我们都测试重复值较少的情况。
- 10w个数据:
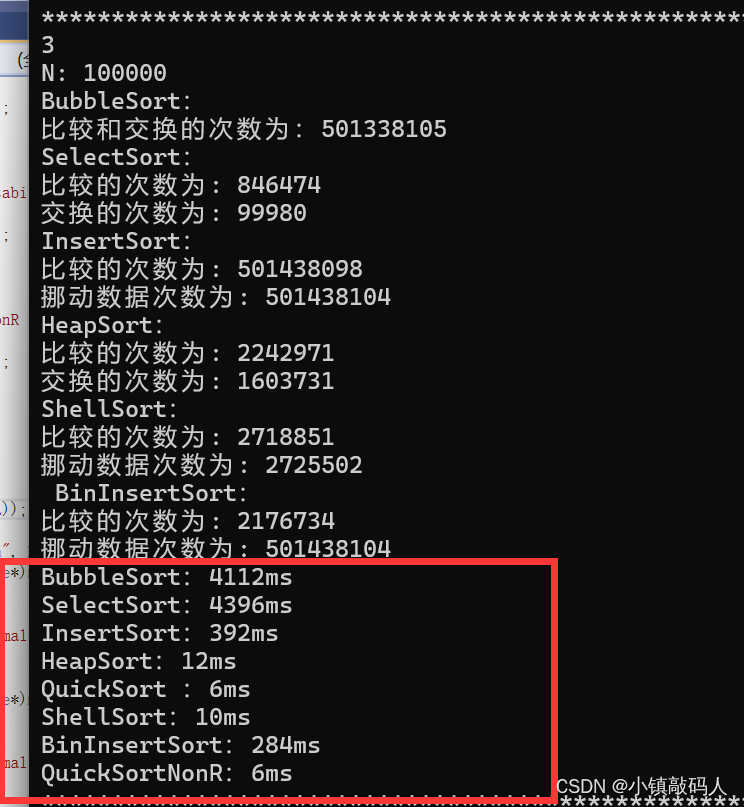
这是重复值较少的情况,重复值较多时,交换类的排序效率会慢很多:
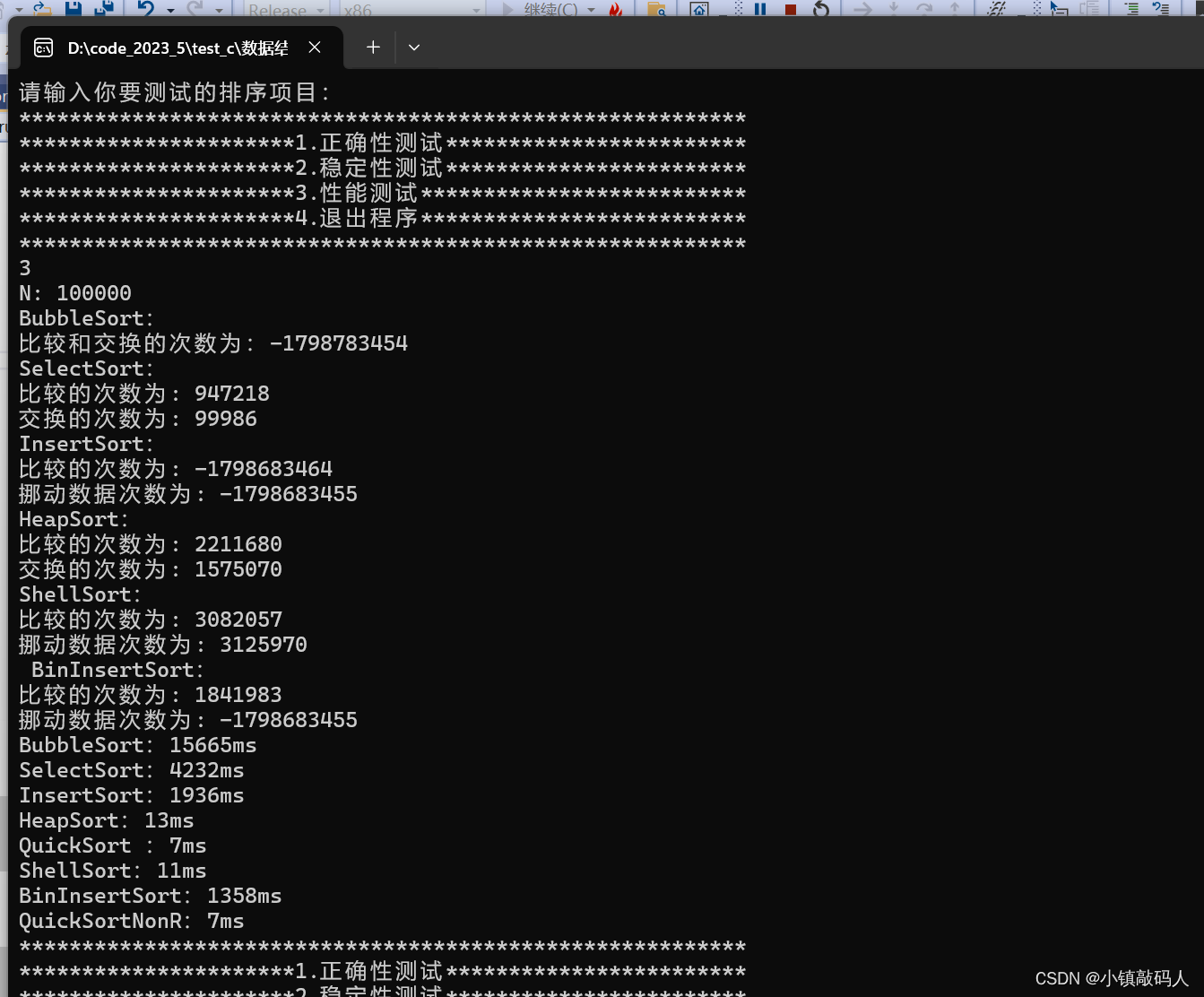
重复值较多的情况下,可以发现对我们交换类的排序是不友好的,比较直观的是冒泡排序,时间来到了惊人的15秒。重复值较多时,有些交换类的排序交换和比较的次数都溢出了(重复值较少时没有溢出)。
同时也可以看出折半插入排序比直接插入排序的优势在于比较的次数大大减少,但是挪动的次数基本没变。

- 100w个数据
数据量太大,我们把 O ( N 2 ) O ( N^2) O(N2)量级的排序给关掉,同样也是重复值较少的情况:
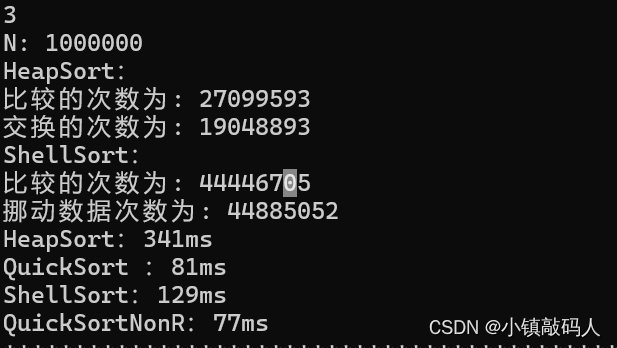
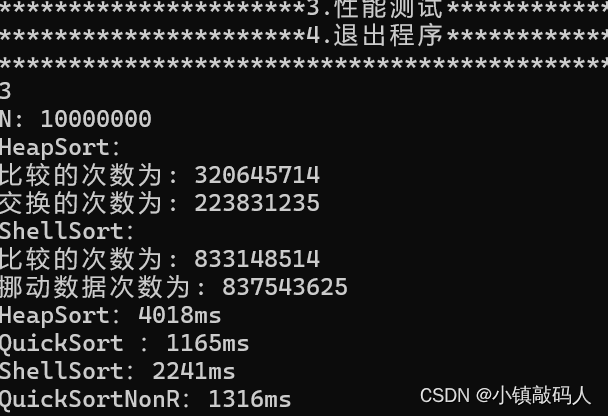
- 1000w个数据
运行结果:


原理及实现)


或OVA(Open Virtual Appliance)格式有什么区别)



)








![[数据集][目标检测]电力工地场景下的人头检测数据集VOC+YOLO格式7035张1类别](http://pic.xiahunao.cn/[数据集][目标检测]电力工地场景下的人头检测数据集VOC+YOLO格式7035张1类别)
