摘要：根据二叉树创建字符串、二叉树的最近公共祖先、二叉树的层序遍历

前言：承接上文，本文继续提供二叉树进阶有关题目的解法。如有错误，烦请指正。

---

目录

1. 根据二叉树创建字符串

题解及代码

2. 二叉树的最近公共祖先

题解及代码

3. 二叉树的层序遍历

题解

代码

---

1. 根据二叉树创建字符串

题源：606. 根据二叉树创建字符串 - 力扣（LeetCode）

给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。

空节点使用一对空括号对 "()" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

示例 1：

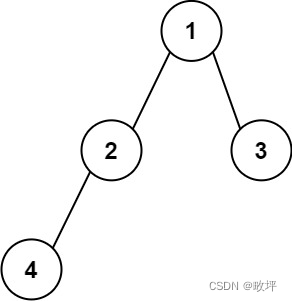
输入：root = [1,2,3,4]
输出："1(2(4))(3)"
解释：初步转化后得到 "1(2(4)())(3()())" ，但省略所有不必要的空括号对后，字符串应该是"1(2(4))(3)" 。

示例 2：

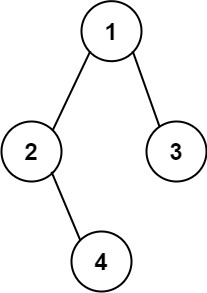输入：root = [1,2,3,null,4]
输出："1(2()(4))(3)"
解释：和第一个示例类似，但是无法省略第一个空括号对，否则会破坏输入与输出一一映射的关系。

提示：

• 树中节点的数目范围是 [1, 104]
• -1000 <= Node.val <= 1000

题解及代码

• 方式一：递归 + 处理括号。对于每个递归的子问题：括号有4种情况，①root()(sub_right)；②root(sub_left)(sub_right)；③root(sub_left)；④root；以上这4种情况可归纳为：（一）sub_right 存在(①②)；（二）sub_right 不存在(③④).

  class Solution {
  public:void _tree2str(TreeNode* rootP,string& ret){if(rootP == nullptr)return;ret += to_string(rootP->val);if(rootP->right != nullptr){if(rootP->left == nullptr)//①{ret += "()";ret += '(';_tree2str(rootP->right,ret);ret += ')';}   else//②{ret += '(';_tree2str(rootP->left,ret);ret += ')';ret += '(';_tree2str(rootP->right,ret);ret += ')';}}else{if(rootP->left == nullptr)//③{_tree2str(rootP->right,ret);_tree2str(rootP->left,ret);}else//④{ret += '(';_tree2str(rootP->left,ret);ret += ')';}      }}string tree2str(TreeNode* root) {if (root == nullptr)return "";string ret;_tree2str(root,ret);return ret;}
  };

• 方式二：模拟递归(“非递归”) + 处理括号（此处建议看过 上一篇二叉树进阶题合集最后三题 对于非递归的思路的讲解之后再看） 

紧承上篇的结尾的总结，则我们可容易得出如下图解：

①进入root层：递归进入 root 层，并判断作左子树是否为空，为空则继续判断右子树；
②返回root层：左子树为空/递归完，判断右子树是否为空，不为空就接着递归右子树；
③第二次返回root层：右子树为空/递归完，判断右子树是否访问完毕，访问完则结束。
关键：区分是第几次返回root层。→ 可以通过一个变量来记录。

class Solution {
public:string tree2str(TreeNode* root) {if (root == nullptr)return "";string ret;stack<pair<TreeNode*,bool>> st;TreeNode* CurP = root;while (CurP || !st.empty()) {while (CurP) {st.push(make_pair(CurP,1));ret += to_string(CurP->val);//cout << "ret += to_string(CurP->val);";if(CurP->left || CurP->right)ret += '(';CurP = CurP->left;}pair<TreeNode*,bool>& topPr = st.top();TreeNode* tp = topPr.first;if (tp->right == nullptr){if(tp->left != nullptr)ret += ")";//左右子树的结点没有任何括号st.pop();//该层递归结束} else // topP右不空{if(topPr.second == 1) //右子树存在且未被访问{ret += ")(";topPr.second = false;CurP = tp->right;}else //右子树存在但被访问完了{ret += ')';st.pop();//该层递归结束}}}//_tree2str(root,ret);return ret;}
};

---

2. 二叉树的最近公共祖先

题源：236. 二叉树的最近公共祖先 - 力扣（LeetCode）

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

题解及代码

方式一：根据最近公共节点的特点来解题。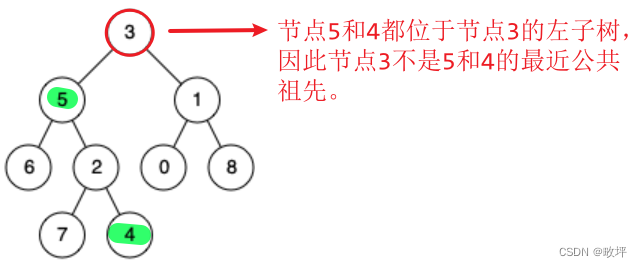
根据题目描述可知：p，q两节点一定分别位于最近公共祖先节点的左子树或右子树（或者其中一个节点本身就是最近公共节点）

class Solution {
public:bool Findsubtree(TreeNode* root,TreeNode* node){if(root == node)return true;if(root == nullptr)return false;return Findsubtree(root->right,node) || Findsubtree(root->left,node);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr)return nullptr;if(root == p || root == q)return root;bool pInLeft = Findsubtree(root->left,p);//p位于root的左子树bool pInRight = !pInLeft;//p位于root的右子树（同：不位于root的左子树）bool qInLeft = Findsubtree(root->left,q);//同上bool qInRight = !qInLeft;//同上if((pInLeft && qInRight) || (pInRight && qInLeft))//若p，q分别位于左右子树，则该层root为最近公共祖先节点return root;if(pInLeft && qInLeft)//如果都位于左子树则得递归到左子树去找最近公共祖先节点return lowestCommonAncestor(root->left,p,q);if(pInRight && qInRight)//如果都位于右子树则得递归到右子树去找最近公共祖先节点return lowestCommonAncestor(root->right,p,q);return nullptr;//按代码运行逻辑不会走到这句，但是这里对返回值的编译检查比较严格。}
};

方式二：找到从根节点分别“走”到p，q节点的路径。在这两个路径中，从p，q节点开始往前看，第一个相等的结点就是最近公共祖先。即：
pathOfp{x,x,x,x,x,a,b,……,p}
pathOfq{x,x,x,x,x,y,z,w,……,q}
关键在于：如何找到这两条路径？
​​答：找到路径中所含的每个节点的特征——该节点的子树中一定含有p或q节点（或者该节点本身就是p或q节点）。→ 找路径的思路：依次递归每个节点，递归到该节点的时候，该节点push入栈，再去递归该节点的左子树和右子树，如果该节点的左子树和右子树中有没有要找的结点，那么该节点不属于路径中的结点，则pop该节点。接着去递归别的节点。

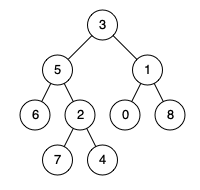
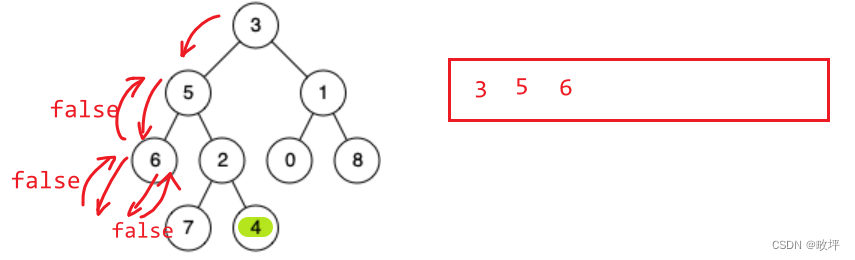如该图所示，目标是从根节点找到节点4。首先，节点3递归左子树到节点5，节点5递归左子树到节点6，节点6的左子树为空未找到节点4，节点6的左子树返回false，节点6的左子树同理返回false，由于节点6的左右子树都为false，即都未找到节点4，则节点6不是该路径中的结点，节点6将被pop出栈，并且，节点6作为节点5的左子树，递归的结果点为false。然后继续递归节点5的右子树。

class Solution {
public:bool FindPath(TreeNode* root,TreeNode* node,stack<TreeNode*>& path){   if(root == nullptr){return false;}path.push(root);if(root == node)return true;if(FindPath(root->left,node,path))return true;if(FindPath(root->right,node,path))return true;path.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr)return nullptr;if(root == p || root == q)return root;stack<TreeNode*> pathOfp,pathOfq;FindPath(root,p,pathOfp);FindPath(root,q,pathOfq);while(pathOfp.top() != pathOfq.top()){if(pathOfp.size() < pathOfq.size()){pathOfq.pop();}else{pathOfp.pop();}}return pathOfp.top();}
};

---

3. 二叉树的层序遍历

题源：102. 二叉树的层序遍历 - 力扣（LeetCode）107. 二叉树的层序遍历 II - 力扣（LeetCode）

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

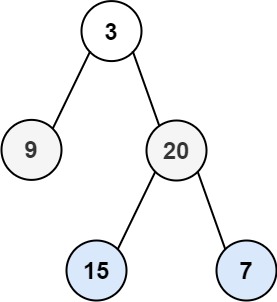输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -1000 <= Node.val <= 1000

题解

C++初阶 | [十] stack 和 queue在该篇文章中的【queue OJ】部分的内容给本题的出了思路。

下面给的代码为思路三的解法。

代码

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {if(root == nullptr)return vector<vector<int>>();vector<vector<int>> ret;size_t levelSize = 0;queue<TreeNode*> qTree;TreeNode* CurP = root;qTree.push(CurP);levelSize = qTree.size();while(!qTree.empty()){vector<int> tmp = {};while(levelSize--){CurP = qTree.front();if(CurP->left){qTree.push(CurP->left);}if(CurP->right){qTree.push(CurP->right);}tmp.push_back(CurP->val);qTree.pop();}ret.push_back(tmp);levelSize = qTree.size();}return ret;}
};

---

END