目录
1.二部图
(1)简单认识
(2)定义
(3)判定定理
(4)定理理解
2.匹配问题
(1)匹配
(2)完备&&完美匹配
(3)hall定理
(4)t条件
(5)随堂测试
3.欧拉图
(1)判定定理
(2)构造性问题
(3)随堂测验
4.哈密顿图
(1)理论背景
(2)必要条件
(3)充分条件
(4)实际应用
(5)随堂测验
5.平面图
(1)平面图定义
(2)平面图的应用
(3) 基本概念
(4)基本定理
(5)极大平面图
(6)极小非平面图
(7)随堂测验
(8)欧拉公式
(9)点着色问题
6.特殊图总结
7.理论来源
1.二部图
(1)简单认识
第一个图是一个拓扑结构,路由器抽离出来构成骨干网,这个图就是一个二部图;图2图3也叫做平面图,图2图3是哈密顿图;

(2)定义
下面的就是二部图的定义:v表示的就是图里面的顶点,E表示的就是图里面的边,我们把这个图里面的点划分为两个部分,也就是v1和v2,这个图里面的所有的边都是连接的v1和v2两组点之间的边,我们就把这个图叫做完全二部图(前提是对于一个无向图而言的);
完全二部图就是建立在简单图的基础上面的(简单图就是没有重边也没有环),v1和v2里面的顶点都是相邻的,我们就把这个图叫做完全二部图;这个完全二部图的表示方法就是Krs里面的r代表的就是v1里面的顶点的数量,s代表的就是v2里面的顶点的数量;在这个情况下面,我们的完全二部图里面的边的数量就是r*s(根据排列组合的相关知识就可以得到);

(3)判定定理
下面的这几个图,我们可以判断是否是二部图,对于下面的三张图,这个二部图的特征就会比较明显,我们很容易辨别出来这个就是二部图,但是对于上面的4张,似乎就没有那么明显了,实际上在这7张图里面,前面的三列,每一列的两张图实际上是同构的(我们可以通过各种变换,翻折手段把这个图还原回去),我们需要有一个简单的判定定理直观的进行判断:无向图要是二部图就不能有奇数圈;
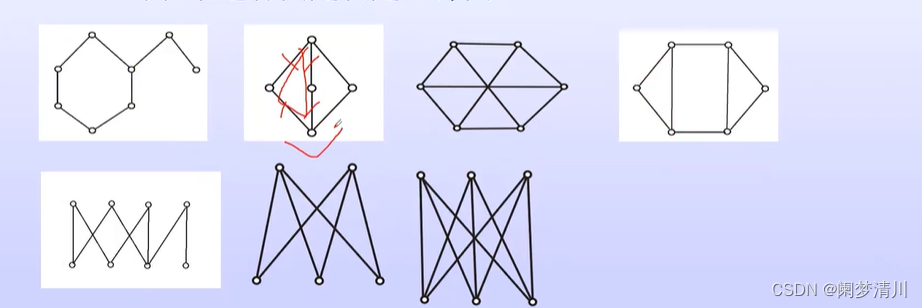
(4)定理理解
上面的这个定理应该如何进行理解:首先这个圈就是初级的回路(从头开始走最后又回到起点),奇数的圈就是这个会路上面的边不可以是奇数条;
拿上面的7张图作为例子,我们的第四张图的左边的一个初级回路就是三条边,不满足这个无向图里面的二部图的判定定理,因此我们就可以知道这个图不是一个二部图(其他的图可以使用这个定理进行验证);
当然我们对于这个判定定理应该有正确的理解:没有奇数圈,分为两种情况,一种就是有圈,但是这个圈全部都是偶数的,还有一种情况就是没有圈,这个也是满足这个判定定理的;
2.匹配问题
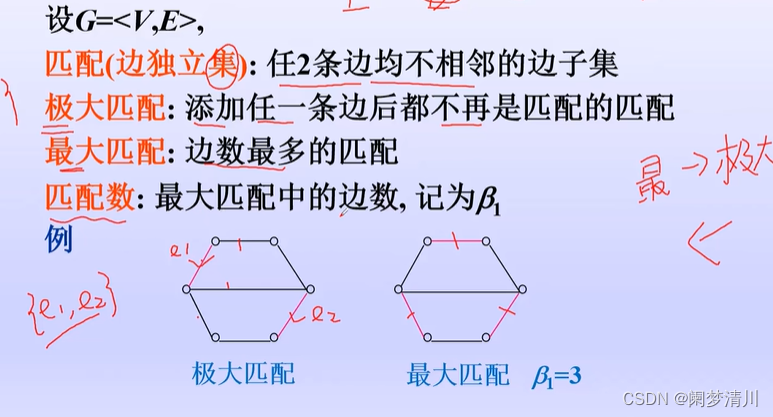
(1)匹配
什么是匹配,匹配就是任意的两条边都不会相邻,极大匹配就是随意的添加上一条边之后就不满足匹配的条件了,最大匹配就是边数最多的匹配,匹配数就是最大匹配情况下的边数;
最大匹配一定是极大匹配,但极大匹配不一定是最大匹配;
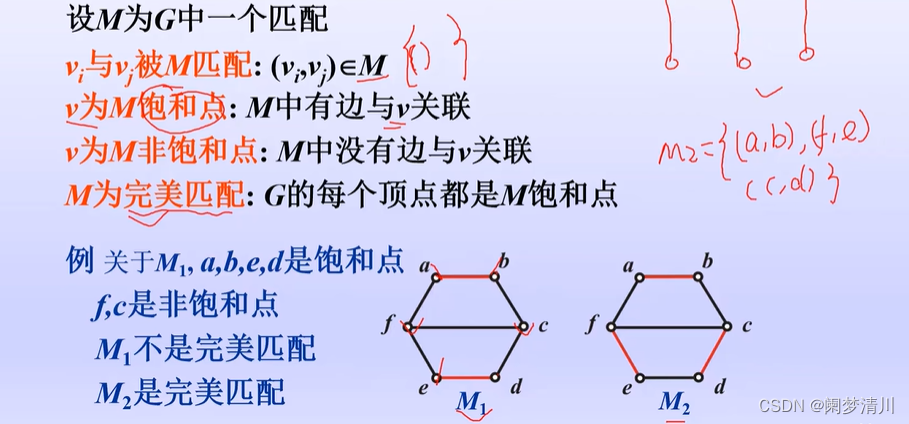
饱和点就是和匹配想回关联的点,非饱和点就是和匹配没有相互关联的点,如果这个图里面的每一个顶点都是饱和的,我们就把这个匹配叫做完美匹配;
完美匹配一定是最大匹配,最大匹配一定是极大匹配;
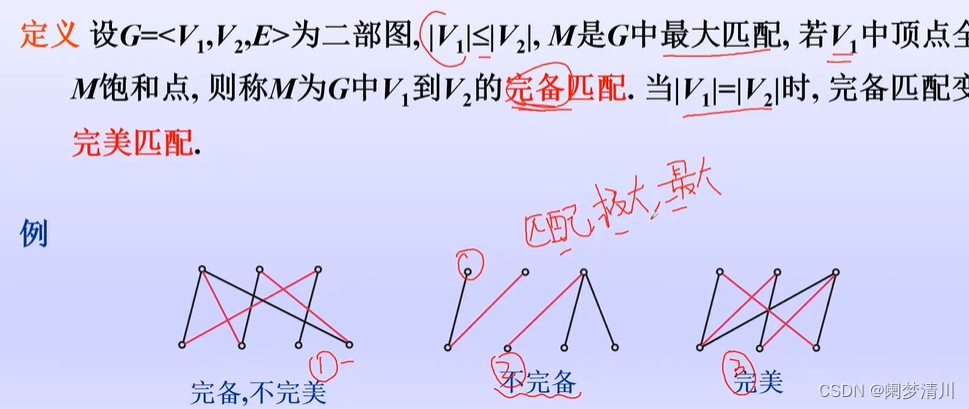
(2)完备&&完美匹配
我们在这个图里面表示的话就是这个红色的边代表的就是匹配,第一个就是完备匹配,但是这个上面和下面的顶点的数量不一样,因此这个就是不完美的,第二个图里面上面的第一个顶点没有匹配,不是饱和点,因此这个不是完备匹配,但是这个是极大匹配,也是最大匹配,因为我们再随意的选择一条边就会破坏这个匹配的条件;第三个图就是一个完美匹配,因为上面的和下面的顶点的数量是一样的,都是3个;(我们只能使用图里面出现的边,不可以人为的添加边)
对于这个匹配的问题,我们可以类比这个大学生找工作,上面的顶点就是代表的大学生,下面的顶点代表的就是招聘公司,只有一个公司找一个学生的时候才是完美匹配,如果最后剩下了一部分的学生,这个就是完备匹配;
(3)hall定理
这个定理就是用来进行这个判断一个图是不是完备匹配,假设上面的三个顶点分别是123,我们选择顶点一的时候,在下面的顶点里面至少有1个和他相连,实际上有3个顶点和他相连,我们选择23这两个顶点,至少应该有2个顶点在下面被匹配(实际上涉及到了4个下面的顶点);
在第二个图里面我们选择1这个顶点,至少有一个顶点和其匹配,这个时候是满足条件的;但是当我们选择12两个顶点,应该至少有2个顶点和其相连,实际上只有一个和他链接,就不符合完备匹配的条件,所以不是完备匹配(这个k,也就是从上面选取的点的个数,这个是可以随机进行指定的,只有在所有的情下都满足,我们才称这个图是完备匹配);

(4)t条件
实际上对于一个图的判断,是否是完备匹配,我们用这个肉眼就可以进行观察,但是这个hall是让这个计算机借助矩阵等等手段进行判断的,相当于这个hall是一种计算机语言判断时使用的方法,而且这个hall是判断一个图形是不是完备匹配的充要条件;
下面的这个t条件,使我们进行判断这个图是不是完备匹配的一个充分条件,因为上面的这个图里面的第三个,上面的最少匹配的边数就是2条,下面的最多匹配的边数就是3条,这个时候其显然是不满足这个t条件的,但是我们已经知道这个图是一个完备匹配,而且是一个完美匹配,可见这个t条件满足的图一定是完备匹配,但是不满足这个t条件的图,不一定不是完备匹配;

我们这个条件是可以降低这个算法的复杂度的,我们可以先使用t条件进行判断,如果满足的话就是一个完备匹配,但是不满足也不一定就不是,这个时候我们再使用hall定理,进行这个充要条件的判定,这样降低算法的复杂度;
(5)随堂测试
这个题目里面的偶图就是二部图的意思,第一个选项里面的圈图需要分情况考虑,奇数的时候就不是二部图,偶数的时候就是二部图;
第二个选项就是二部图的判定定理,也就是没有奇数圈的图;
第三个选项就是方体图,使用Q进行表示,方体图一定是二部图,轮图使用W表示,轮图一定不是二部图(因为轮图里面有三角形);
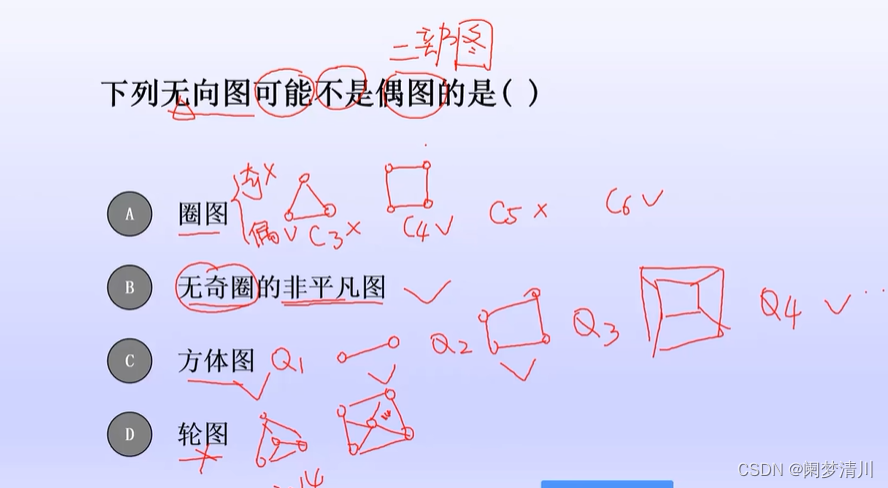
Kn就是完全图的意思,n为1或者2的时候就满足这个二部图的条件,其他的时候就不是二部图,因此Kn有的是二部图,有的不是二部图;轮图一定不是二部图;
3-正则图就是每个顶点的度是3的图,这个K4就是一个这样的图,每个顶点的度就是3,这个时候他不是二部图,但是像右下角画的这个正六边形就是一个3-正则图而且也是二部图;

3.欧拉图
(1)判定定理
这个判定定理我们首先要划分为两大类,一类就是有向图是不是欧拉图,一类就是无向图是不是欧拉图,这个无论是有向图,还是无向图,都包括欧拉图的判定定理(欧拉回路),以及班欧拉图的判定定理(有欧拉通路,但是没有欧拉回路的图);

(2)构造性问题
我们上面使用定理进行判断这个图是不是欧拉图,讨论的就是属于存在性问题,我们找出这个通路,讨论的就是构造性问题,我们的方法就是使用弗里德算法,选择一个奇数度的顶点,没有拘束读的顶点的话,就随机的选择一个,然后开始走,优先选择没有桥的,如果只剩下桥,我们再走桥,依次进行下去,直到走完最后一个顶点;
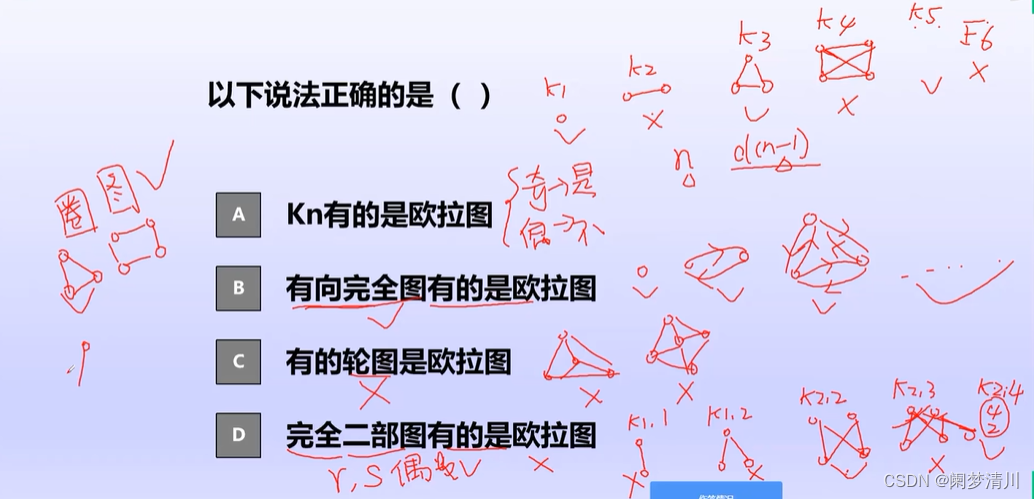
(3)随堂测验
首先应该知道这个圈图至少有3个顶点,轮图至少有4个顶点,知道这些图是怎么画的;
Kn就是完全图,n是奇数的时候就是欧拉图,否则就不是欧拉图,有向完全图是欧拉图(因为每个顶点的入度都等于出度);
轮图一定不是欧拉图,因为轮图的外面的顶点的度都是奇数的,不符合这个欧拉图的判定定理;
完全二部图要想是欧拉图,需要满足的就是这个rs都是偶数,rs分别代表的就是两个集合里面的节点的个数;圈图一定是欧拉图(圈图就是外面的一圈,所以一定是欧拉图);
4.哈密顿图
(1)理论背景
哈密顿图就是经过所有的顶点的图,这个哈密顿图的判定现在是属于NPC问题,就是没有最优的解决方案,我们可以找到他的充分条件和必要条件,但是现在也没有找到充要条件,因此这个问题现在是图论的未解之谜之一;
(2)必要条件
我们判断一个图是不是哈密顿图使用的这个就是他的必要条件的逆否命题,p(G-V1)代表的就是删除v1这个集合之后剩下的图的分支联通数,当这个分支联通数大于这个删除的节点的个数,我们就可以判断这个图不是哈密顿图;

(3)充分条件
n小于3的时候,也就是说节点的个数小于3的时候,任意不相邻的节点度数和大于n-1就可以组成哈密顿通路,n>3的时候,任意不相邻节点度数和大于n就可以组成哈密顿回路;

(4)实际应用
这个现实中的实际问题就是判断是否可以组成哈密顿回路的问题,条件就是任意的两个顶点度数和大于n,这个里面的n代表的就是节点的个数,d(v1)+d(v2)>=8因为这个每个人至少可以和4个人进行交谈,两个的和就是8,因此这个符合哈密顿回路的条件,可以满足;

(5)随堂测验
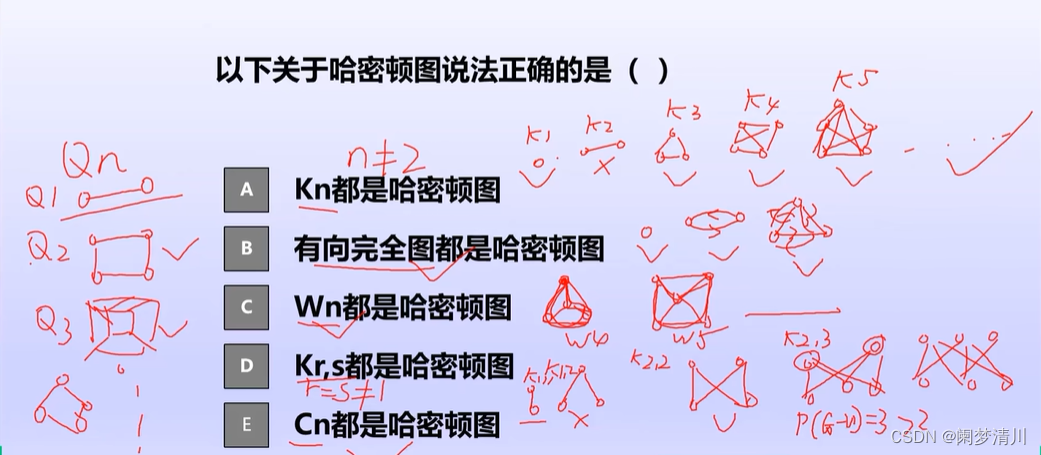 Kn只有n不是2的时候才是哈密顿图,W指的是轮图,轮图全部都是哈密顿图,Krs在r==s的时候是哈密顿图,Cn指的是圈图,全部是哈密顿图,Qn指的是方体图,全部是哈密顿图;
Kn只有n不是2的时候才是哈密顿图,W指的是轮图,轮图全部都是哈密顿图,Krs在r==s的时候是哈密顿图,Cn指的是圈图,全部是哈密顿图,Qn指的是方体图,全部是哈密顿图;
5.平面图
(1)平面图定义
平面图就是这个图里面的边不相交的画在这个平面上面,我们就把这个图叫做平面图,这个平面图是最本质的图形,它本身是可以有相交的,但是我们自己经过这个挪动之后就不会想交了,这个挪动之后的图就叫做平面嵌入,在下面的这个图里面,图3就是一个平面图,虽然这个图看上去好像这个边和边之间有相交的,但是我们挪动之后,挪成为了像图4这样的图,这个实际上就是图3经过挪动之后产生的,这个图4我们就叫做平面嵌入;

(2)平面图的应用
下面的就是这个芯片的抽象模型,上面可见的线都是裸线,这些线之间是不可以交叉的,但是我们平常的线外面都是有一层物质保护的,所以之间是可以相互缠绕的,但是这个芯片里面的裸线之间一旦相互交叉就会短路,这个要想不交叉,就要符合平面图的相关理论;

(3) 基本概念
平面图的顶点,边和面(被分割的平面),平面图每个被分割的面的外围的边叫做边界,边的数量叫做次数,记作deg,我们把这个外部的面叫做外部面,里面的所有被分割的面叫做内部面;
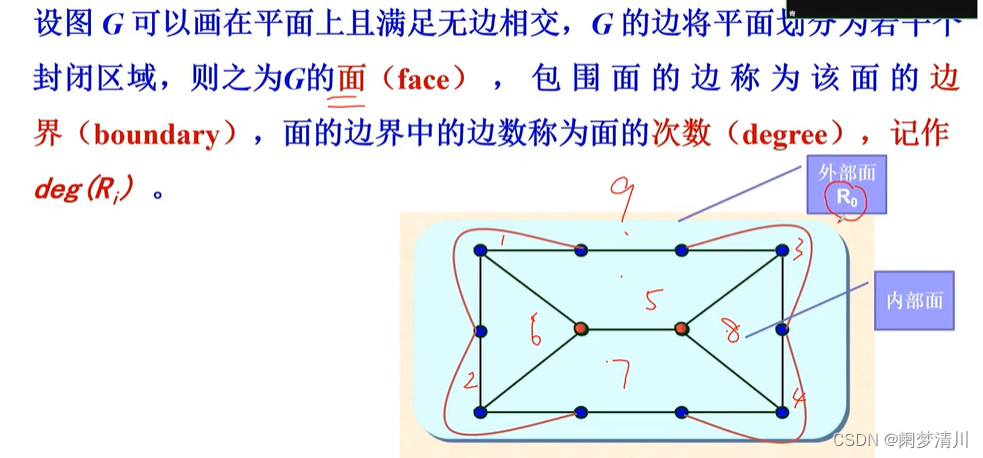
我们再进行这个算面的次数的时候,需要注意的就是这个里面的桥,这个桥是按照2次来进行计算的,本来这个外部面的次数是6,加上这个桥的两次就是8;
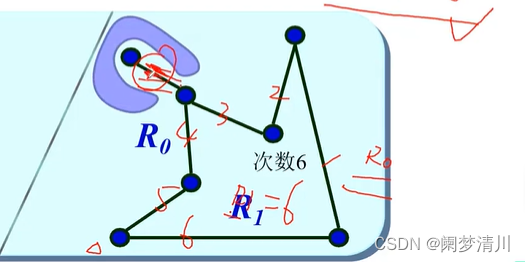
(4)基本定理
平面图的每个面的次数是边数的两倍,因为每个边都关联了两个面,而且这个就算是桥的话,虽然只会关联一个面,我们计算这个次数的时候把这个桥的次数按照2进行计算的;

(5)极大平面图
我们可以通过一个简单的游戏引入这个简单平面图的概念,这个游戏就是添加边,前提是这个图是一个简单图(无重边,没有环),这个样的话,第一个图就没有办法继续添加边,第二个图还是可以添加的,第三个图也是可以继续添加的;
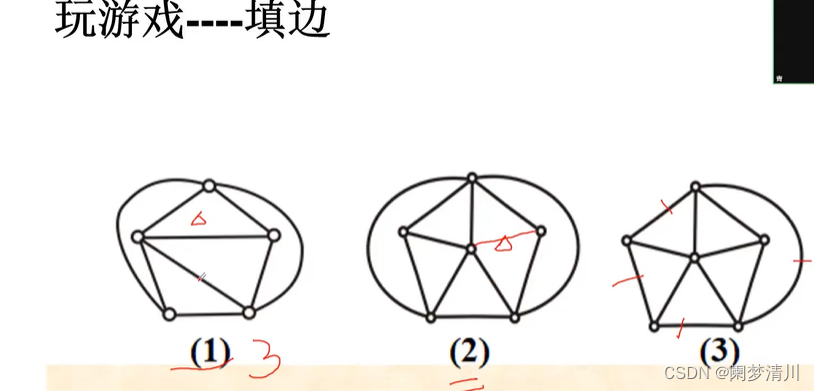
我们通过观察这些图的特征就可以发现,不可以继续添加边的图就是每个面的这个次数都是3,这个时候如果再想添加边,就只能是重边或者是环了,但是这个题目要求就是平面图,所以我们没有办法继续添加边,但是想这个图2,这个是有一个面的次数是1,不是三角形的,我们可以继续添加边,图3最外面的那个面的次数是4,因此也是可以继续添加边的;

通过上面的游戏也就引出了这个极大平面图的定义,就是这个不能再往这个图上面添加边了,这个图就叫做极大平面图,极大平面图的充要条件就是任何的一个面的次数都是3;
(6)极小非平面图
我们上面学习了极大平面图就是只要再添加一条边就不是平面图了,我们称这样的平面图叫做极大平面图,我们前面已经知道K5和K33都不是平面图,但是我们去掉这个里面的一条边就构成了平面图,我们称这种本身不是平面图,但是去掉一条边之后就构成平面图的图形叫做极小非平面图;
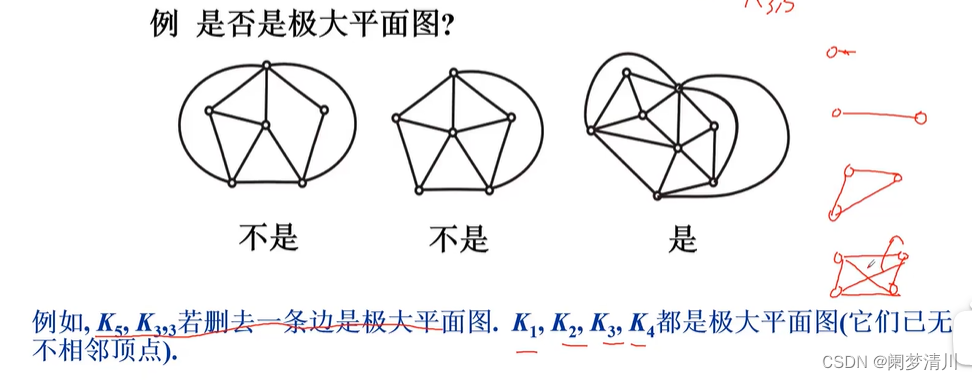

(7)随堂测验
首先我们需要知道的就是这个正则图定义是每个顶点的度数都是一样的;
方体图,轮图和圈图都是平面图,完全图在n=1234的时候是平面图,其他的情况下不是平面图,二部图想这个k33就不是一个平面图,正则图里面也是有的是,有的不是,K5就是一个正则图,因为这个k5的每个顶点的度都是4,但是这个图是一个典型的非平面图;
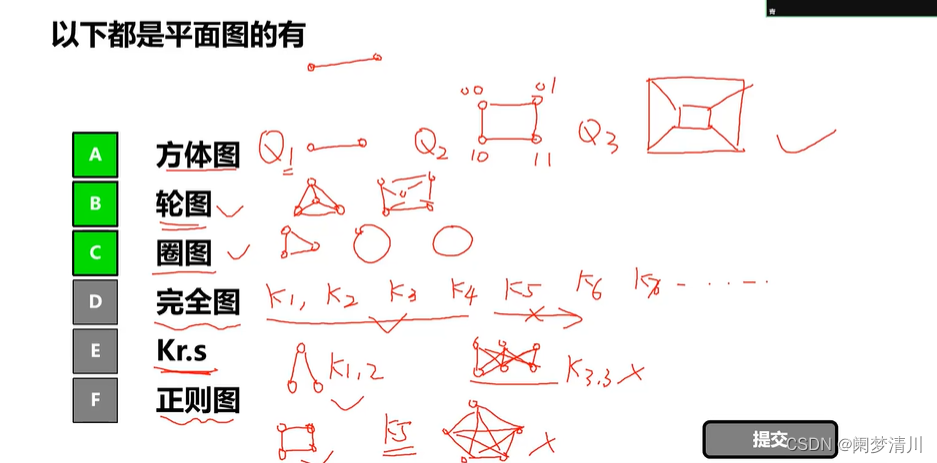
(8)欧拉公式
顶点数+面数-边数=2
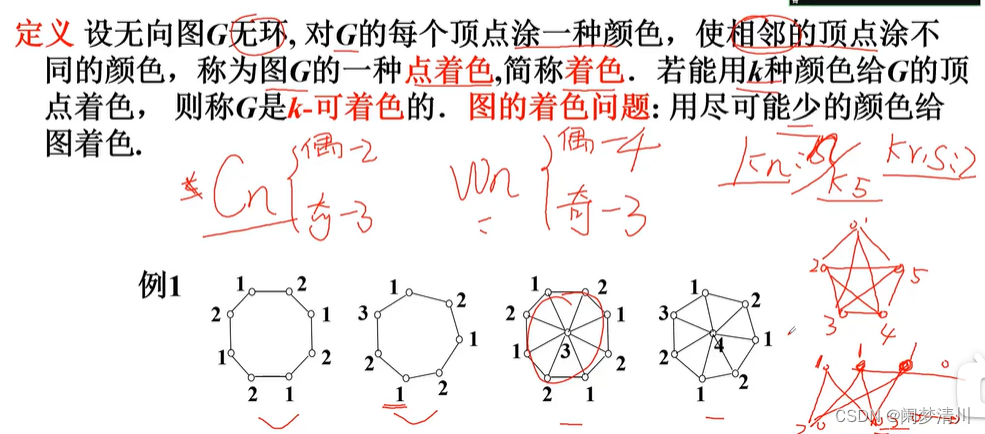
(9)点着色问题
圈图Cn当这个n是偶数的时候需要两种颜色,当n是奇数的时候,需要的就是三种颜色;
对于这个Wn的轮图,偶数的时候需要4种颜色,奇数的时候需要三种颜色,对于完全图,n是几,就需要几种颜色,对于二部图,我们需要的颜色就是r个,r就是第一个节点集合里面的元素的个数
6.特殊图总结
(1)二部图:无奇数圈,欧拉图的这个有向图和无向图的判定定理,哈密顿图的充分必要条件,必要条件是从这个抠出顶点之后的这个联通数的角度进行判断的,联通数小于这个扣除的顶点的个数才是哈密顿图(实际上我们进行判断的时候使用的是他的逆否命题);一个是从这个任意的两个顶点的度数的和大于这个顶点的总个数,就符合这个哈密顿回路的充分条件;
(2)平面图就是这个边不相互缠绕,学习了极大平面图和极小非平面图,了解欧拉图的公式,对偶图,例如图一和图二,图一的定点数等于图2的边数,图2的边数等于图1的顶点数;
(3)原图的面数等于对偶图的顶点数,原图的边数等于对偶图的边数,原图如果有桥,对偶图就会有环,原图如果有环,对偶图就会有桥;

7.理论来源
以上内容来自于B站的一位老师,认为很值得推荐给大家,这个老师的讲解以及上面同学们的总结还是很值得我们学习的,下面的是对应的讲解链接,同学们可以自行进行学习;
离散数学:二部图、欧拉图、哈密顿图_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1AP4y197wd/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=a432cb5e896a2b96961d1f73a6ebe0ca离散数学 特殊的图--平面图_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1AP4y197wd/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=a432cb5e896a2b96961d1f73a6ebe0ca离散数学 特殊的图--平面图_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1hM41167ad/?p=12&spm_id_from=pageDriver
https://www.bilibili.com/video/BV1hM41167ad/?p=12&spm_id_from=pageDriver


)



—— 神经网络语言处理)





)




 v13.1安装教程)

)