主要通过单调队列来解决滑动窗口问题，得到滑动窗口中元素的最大值和最小值。
目录
前言
一、滑动窗口
二、算法思路
1.滑动窗口
2.算法思路
3.代码详解
三、代码如下
1.代码如下
2.读入数据
3.代码运行结果
总结
前言
主要通过单调队列来解决滑动窗口问题，得到滑动窗口中元素的最大值和最小值。
提示：以下是本篇文章正文内容，下面案例可供参考
一、滑动窗口
给定一个大小为 n≤1000000的数组。
有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。
你只能在窗口中看到 k个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子：
该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。
| 窗口位置 | 最小值 | 最大值 |
|---|---|---|
| [1 3 -1] -3 5 3 6 7 | -1 | 3 |
| 1 [3 -1 -3] 5 3 6 7 | -3 | 3 |
| 1 3 [-1 -3 5] 3 6 7 | -3 | 5 |
| 1 3 -1 [-3 5 3] 6 7 | -3 | 5 |
| 1 3 -1 -3 [5 3 6] 7 | 3 | 6 |
| 1 3 -1 -3 5 [3 6 7] | 3 | 7 |
你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数，代表数组的具体数值。
同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出，从左至右，每个位置滑动窗口中的最小值。
第二行输出，从左至右，每个位置滑动窗口中的最大值。
输入样例：
8 3
1 3 -1 -3 5 3 6 7
输出样例：
-1 -3 -3 -3 3 3
3 3 5 5 6 7二、算法思路
1.滑动窗口
我们先解释一下滑动窗口，以上述测试样例，滑动窗口的大小为3。
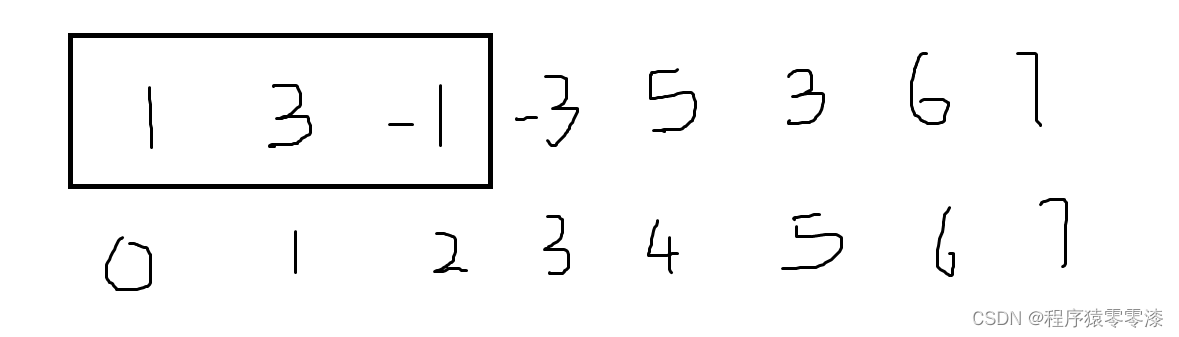
图1.1滑动窗口
当我们继续遍历元素的时候，为了保证窗口内一直是3个元素，每加入一个元素，就要剔除一个最左边元素，直到遍历到最后一个元素，这就是滑动窗口。
2.算法思路
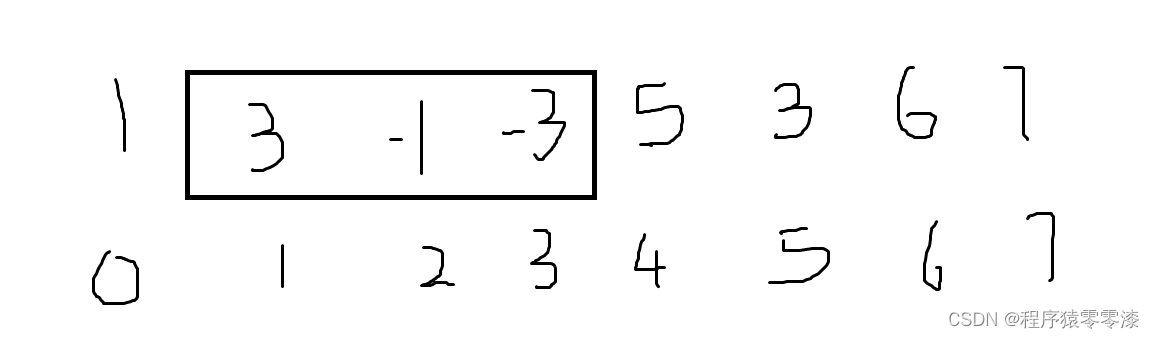
图2.1思路模拟
我们先来求当前滑动窗口的最小值。我们以 图2.1中的滑动窗口为例，求此窗口的最小值从图中可以得到是-3，它前面的3和1是不可能被当作答案输出的；当有两个索引i < j（即i在j的左侧），且存在arr[i] >= arr[j]，那么当滑动窗口向右移动，i还在滑动窗口内，那么j一定还在窗口内（由于i在j的左侧所保证的）。因此由于arr[j]的存在，那么arr[i]就一定不会被当作最小值答案输出，那么我们就可以将arr[i]永久移除。
那么我们可以用一个队列来存储还没有被移除的元素的下标，在队列中，这些元素下标按照从小到大的顺序被存储在队列当中，并且有一个特性，保持其中索引对应的元素是单调递增的。那么我们当前滑动窗口中最小值的元素就是队列中队头元素对应的数组元素。
当滑动窗口右移时，我们需要把一个新元素放入队列当中。
为了保持队列中的下标对应的元素是单调递增的特性，我们需要将新元素与队尾元素进行比较，如果队尾元素对应的数组元素大于等于新加入的元素，那么我们就可以将队尾元素永久的剔除，将他弹出队列，重复的执行上述操作，直到队列为空或者队尾元素小于新加入的元素。
当然在窗口向右移动的过程中，我们还需要不断地从队列中弹出队头元素，来保证队列中的下标都是滑动窗口中的元素的下标。
3.代码详解
我们引入一位整型数组arr来存储元素，用一维整型数组queue来存储滑动窗口内元素的下标。引入一个整型变量k来表示滑动窗口的长度，用整型变量head表示队头指针，rear表示队尾指针。
通过一个for循环来遍历每个元素，同时我们要来判断此时是否需要弹出队头元素，队尾元素的下标就是此时遍历的元素i，那么队头元素的下标就为 i - k + 1，如果i - k + 1大于队头存储的元素（队列中存储的是元素的下标）即i - k + 1 > queue[head]，此时就说明要弹出队头元素来保证队列中的元素个数为k个；然后我们又需要将新加入的元素来与队尾元素对应的数组元素进行比较，如果存在队尾元素对应的数组元素大于等于新加入的元素即arr[queue[rear]] >= arr[i]，就说明队尾元素对应的数组元素不可能被当作滑动区间的最小值被输出，就可以将队尾元素弹出，直到队列为空或者队尾元素对应的数组元素小于新加入的元素。接下来将新加入的元素的下标进行入队操作。
最后当滑动窗口中有k个元素的才会输出答案，那么当要输出第一个答案的时候滑动窗口的元素对应的数组下标一定是k-1，后面每加入元素下标肯定是比k-1要大的，故只有下标大于k-1的时候才会输出一个答案，求最小值我们只需要输出一下队头元素对应的数组元素即可。
求滑动窗口的最大值我们只需要重复一下上述操作，将队列中的元素保证为单调递减即可，将新加入的元素与队尾元素对应的数组元素进行比较，如果新加入的元素大于等于队尾元素，那么就说明队尾元素对应的数组元素是小的值，不可能被当作滑动窗口的最大值进行输出，就弹出队尾元素。最后滑动窗口的最大值还是队列中的队头元素对应的数组元素。
三、代码如下
1.代码如下
import java.io.*;
import java.util.*;
public class 滑动窗口 {static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static int N = 1000010;static int[] arr = new int[N];//队列里面存的是下标static int[] queue = new int[N];public static void main(String[] args) {Scanner sc = new Scanner(br);int n = sc.nextInt();int k = sc.nextInt();int head = 0;int rear = -1;for(int i = 0;i < n;i++){arr[i] = sc.nextInt();}for(int i = 0;i < n;i++){//判断是否弹出队头元素，且每次就弹出一个元素，就写if就可以了if (head <= rear && i - k + 1 > queue[head]){head++;}//保证队列中元素的下标对应的元素是一个递增序列，队尾元素大于等于新加入的元素就弹出队尾元素while (head <= rear && arr[queue[rear]] >= arr[i]){rear--;}//新元素入队queue[++rear] = i;//因为这道题是当滑动窗口中有k个元素的话才会输出一个答案，那么第一个答案对应的元素的下标肯定是k-1，后续要输出的答案的元素的下标肯定比k-1大if(i >= k-1 ){pw.print(arr[queue[head]]+" ");}}pw.println();head = 0;rear = -1;for(int i = 0;i < n;i++){if (head <= rear && i - k + 1 > queue[head]){head++;}//保证队列中元素的下标对应的元素是一个递减序列，队尾元素对应的下标元素小于等于新加入的元素就弹出队尾元素while (head <= rear && arr[queue[rear]] <= arr[i]){rear--;}//新元素入队queue[++rear] = i;//因为这道题是当滑动窗口中有k个元素的话才会输出一个答案，那么第一个答案对应的元素的下标肯定是k-1，后续要输出的答案的元素的下标肯定比k-1大if(i >= k-1 ){pw.print(arr[queue[head]]+" ");}}pw.flush();}
}
2.读入数据
8 3
1 3 -1 -3 5 3 6 7
3.代码运行结果
-1 -3 -3 -3 3 3
3 3 5 5 6 7 总结
主要我们理解如何保持单调队列中元素的特性，知道如何维护队列即可，这是这道题的关键所在。
