g-h 过滤器

g-h 滤波器百科介绍。

之前的翻译大家，我看都没什么阅读量，可能大家都不是很想看（估计也是我英文太水）。那么这篇博客我就先暂停直接翻译原文，而是直接说一下自己的理解。

本文章背后的书的详细介绍可以查看 链接

从头开始认识 g-h 过滤器

作者通过对使用含有误差的秤（现实世界的秤都不可能百分之百准确）测量自己的体重引出了 g-h 过滤器的概念。
这也是一个相当重要的概念，对后面的要学习的各种滤波算法起到了非常关键的思想上的引导。
g-h过滤器的核心思想就是对预测值和实际的测量值找到一个比重，来使得实际的评估值更加能接近最真实的体重。
下面的图就是如何对体重进行评估的方式描述。

这里的 last_estimate 是值上一次的评估值， estimate 是当前的评估值，prediction 是通过上一次的评估值对当前的预测值，measurement 是当前的测量值。这里的值全部是指作者要测量的目标，也就是体重。

这时如果单纯的只考虑测量值和预测值之间的关系，选择一个系数来分配他们的关系，比如下面的式子。

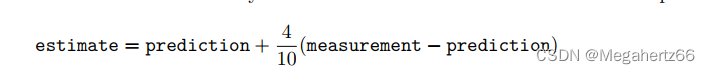
这个式子如果用代码来实现只需要用两行，变量名字起的很好，十分易懂。

        # 预测新的重量，gain_rate 就是对体重的预测变化predicted_weight = estimated_weight + gain_rate * time_step# 对过滤器的状态进行更新 ， 这里的 scale_factor 就可以理解为上面式子的 4/10estimated_weight = predicted_weight + scale_factor * (measurement - predicted_weight)

在这种情况下因为没有考虑预测值与前一次评估值的变化关系，导致这种办法只在我们设计滤波器的时候对变化关系做出了正确设置的时候才会产生作用。
比如假设每天我们都会增加体重1lbs（磅），如下图所示：

这个时候滤波器表现的很好。但是如果我们对于预测值的变化设置错误的情况下，图形看起来就不会有这种比较好的效果了。
下图就是在代码中我们假设我们的体重仍是每天增长 1 lbs（磅），但是评估值和预测值之间的关系设置为 -1 的时候的样子。

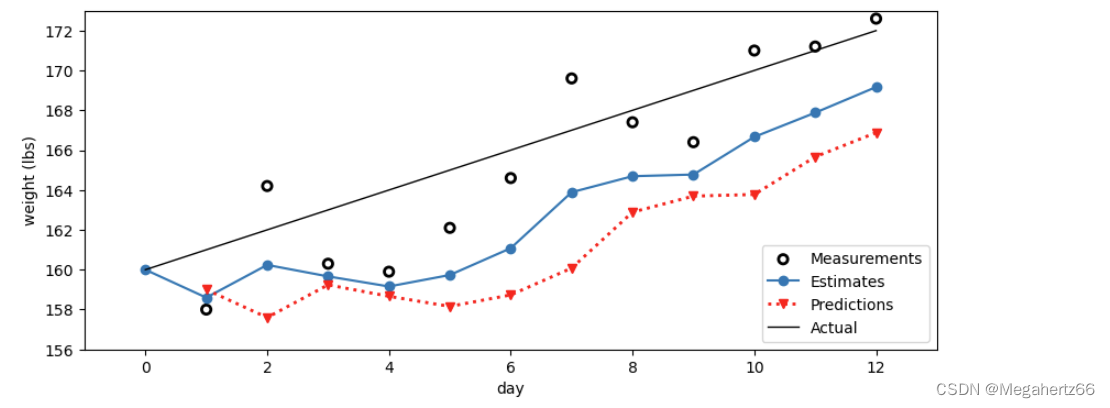
为什么会产生这样的效果呢~ 让我们再看看上面决定评估值的代码，当 gain_rate 为 -1 时，也就意味着，每次 prediction 也就是预测值都会比前一次的 estimation 值少 1。这样看图像看起来就像是 红色线始终大幅度落后于圆点，导致我们最终需要的评估值偏离测量值较大，而且跟随性差。

既然是对于评估值的设置出现了错误，是因为之前只是单纯的添加了变化率而没有考虑对于变化率的调整。 那么就再加入一个参数用于调整预测值与前一次测量值的权重。

这里对上面的式子进行一下解释，新的变化率时根据上一次的变化率进行推算得出的。 predicted weight 是根据上一次的变化率推断出的预测值，而 measurement 是本次实际的测量值，而分母 1day 则是对对应了时间上的变化量。下面就是书中的 python 代码，运行即可得到上面的图像。

weight = 160.  # initial guess
gain_rate = -1.0  # initial guesstime_step = 1.
weight_scale = 4./10
gain_scale = 1./3
estimates = [weight]
predictions = []for z in weights:# prediction stepweight = weight + gain_rate*time_stepgain_rate = gain_ratepredictions.append(weight)# update step    residual = z - weightgain_rate = gain_rate + gain_scale   * (residual/time_step)weight    = weight    + weight_scale * residualestimates.append(weight)gh.plot_gh_results(weights, estimates, predictions, [160, 172])

理解 g-h 过滤器要点

作者还总结了关于 g-h 过滤器关键的四点

1. 通过多个数据是要比单个数据整体来说更加的准确，所以说没有理由放弃任何哪怕是不准确的数据。
2. 选择两个数据之间的值，往往能获得更加的准确性。
3. 根据当前的估计和我们认为它会改变的程度，预测下一个预测值和变化率。
4. 然后选择新的估计作为预测和下一个测量之间的一部分，根据每个测量的准确度进行缩放。

接下来的是对 g-h 过滤器的总结 ：

初始化(Initilization)：

1. 为过滤器选择合适的初始化状态
2. 初始化我们对于未来状态的信念(belief)

预测(Predict)：

1. 使用系统行为(system behaviour)来预测下一时间的状态。
2. 调整信念(belief)以考虑在预测过程中的不确定性。

更新(Update)：

1. 获得一个测量值，以及与之相关的对其准确性的信念(belief)。
2. 计算预测值与实际测量值之间的差值(residual)。
3. 新的评估值在预测值和测量值的直线上选择。

这里对更新步骤中第三点再进行一些解释，这里的意思就是像下图中黄色框中一样。在 measurement， prediction之间选择 estimate的值。

对于 g & h 的选择

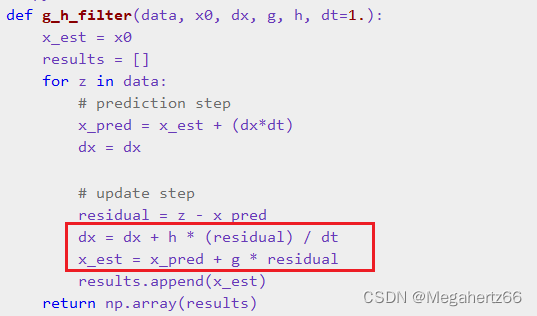
通过上面的章节，我们可以知道所谓的 g 和 h 就是对预测值的调整和对评估值的调整。在这里作者给出了一个 g-h filter 的python 的代码实现，并且可以使用这个函数来验证 g 和 h 的变化对过滤器实际表现的影响。

def g_h_filter(data, x0, dx, g, h, dt=1.):x_est = x0results = []for z in data:# prediction stepx_pred = x_est + (dx*dt)dx = dx# update stepresidual = z - x_preddx = dx + h * (residual) / dtx_est = x_pred + g * residualresults.append(x_est)return np.array(results)

这个函数参数 data 是用来输入需要过滤的数据， x0 是我们选取的初始化的值，dx 则是对开始信念(belief)也可以理解为开始时的变化率。g 和 g 就是这个过滤器需要根据不同的数据特省进行调整参数。dt 是产生变化的单位时间。

对于这个实现的 g-h 过滤器，作者还给出了几种不同情况下的例子：

不合适的初始化值

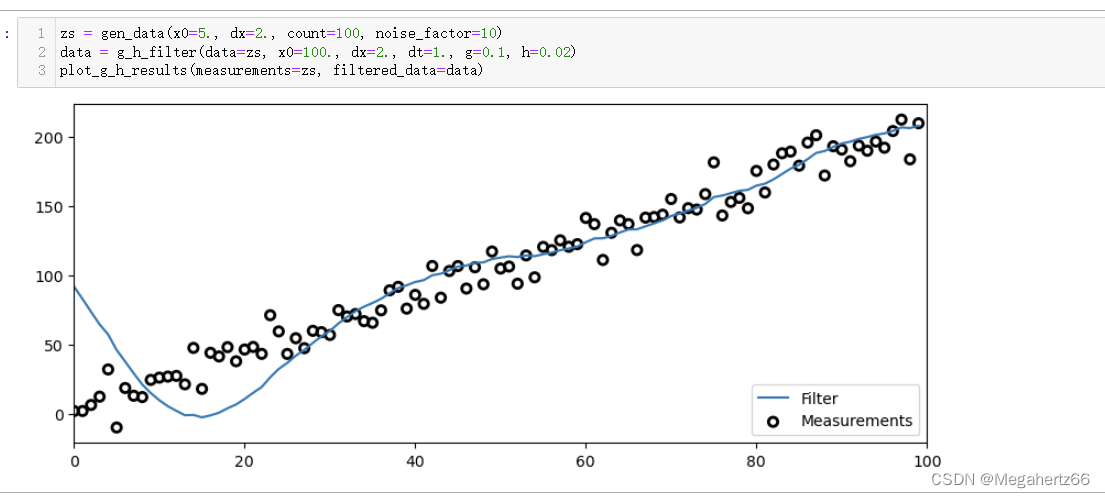
从这个图里面本该将过滤器的初始化值设置为 0 左右，实际上却设置为了 100，能看到在 20 左右出现了比较大的振铃现象(Ringing)。振铃现象的含义是，信号不断地在过冲(Overshoot)和下冲(Undershoot)。

比较极端的噪声

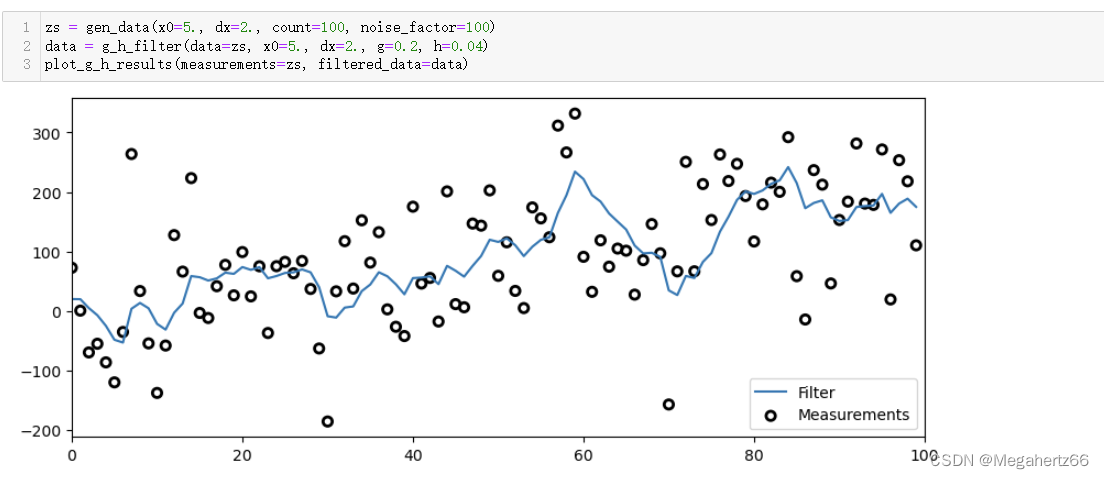
在这种情况下，由于噪声太大了导致过滤器得到的最终结果和一条平滑的线相距甚远。

加速度不匹配

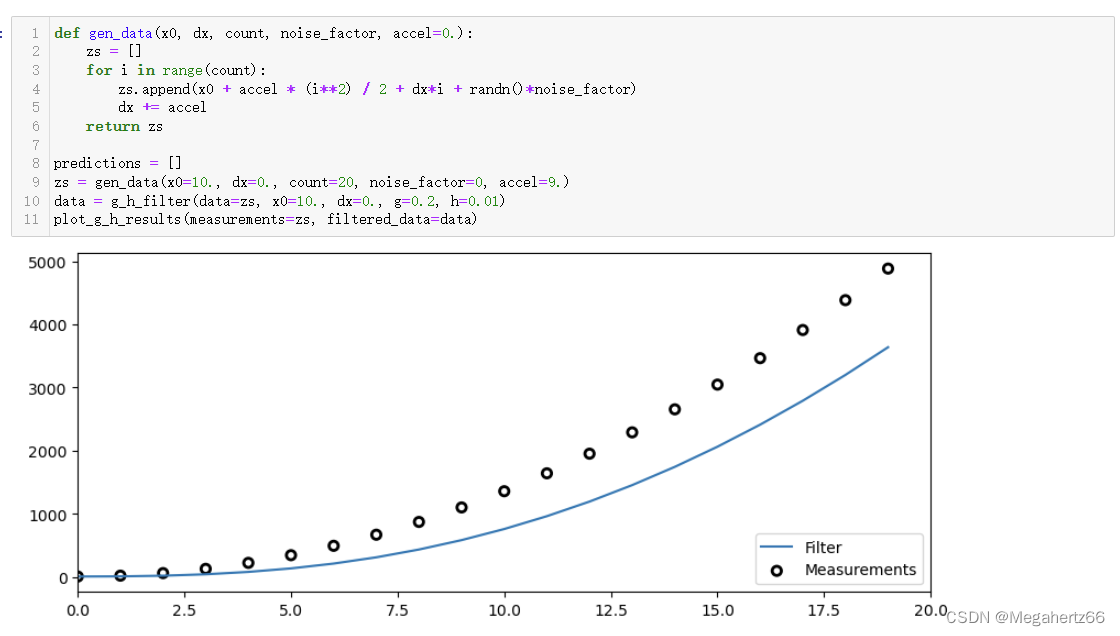
再上图中，看起来过滤器的自傲过很好，但是实际上产生的曲线一直实在测量值之下。

改变参数 g

上面的例子可以看出当 g 的值越大，通过滤波后的曲线就越接近测量值。当 g=0.8 时几乎就是直接追着测量值在跑，几乎没有忽略掉任何的噪声。但是当 g=0.1时，滤波出来的数据看起来非常的平滑，但是几乎没有考虑测量值的变化信息。

这里也是可以看出当g越小的情况下对于测量值的跟踪越好。

改变参数 h

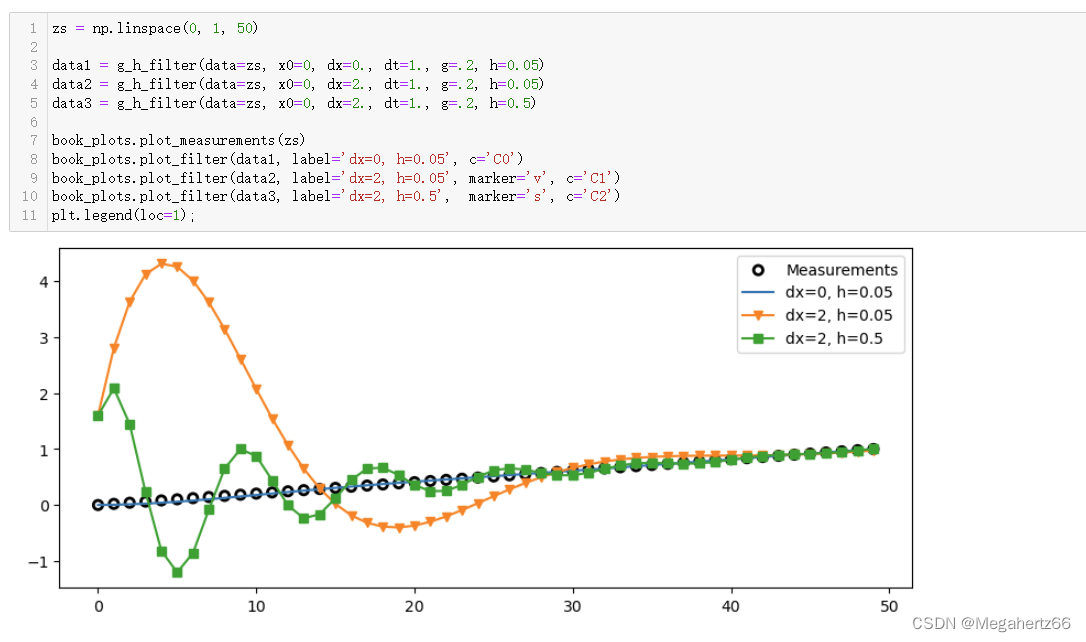
到这里感觉调整 g 和 h 参数的效果有点像啊，看起来都是改变滤波器对测量值的跟随性。但是实际上并不是这样的，可以再看一下前面对于 g 和 h 含义的代码。

h 决定了对于预测值的变化，g 决定了预测值和测量值的权重。所以此处更改 h 的值，就是在修改对于预测值的改变速度。所以上图中橙色线所代表较小的 h 值，就导致了橙色线变化的速度并不快，或者说时比较滞后。而绿色线拥有较大的 h 值，现象是变化非常快速，但是相较于橙色线却产生了比较多次的振铃现象。

不要为了好看的数据写入错误的 g & h 的值

如果单纯的为了过滤出来的曲线好看，不考虑实际需求，将 g 和 h 设置的都非常小，就会得到一根非常平滑的线，但是这并没有实际的意义。