0 .概述
介绍下二叉树重构
1. 遍历序列
任何一棵二叉树我们都可以导出先序、中序、后序遍历序列。这三个序列的长度相同,他们都是由树中的所有节点依照相应的遍历策略所确定的次序,依次排列而成。
若已知某棵树的遍历序列是否可以忠实地还原出这棵树地拓扑结构?什么情况下可以?什么情况下不可以?如果可以,具体又应该使用什么方法?
2. 先序 | 后序 + 中序
结论:只需中序遍历序列再加上先序与后序遍历序列之一,即可忠实还原二叉树地完整拓扑结构。
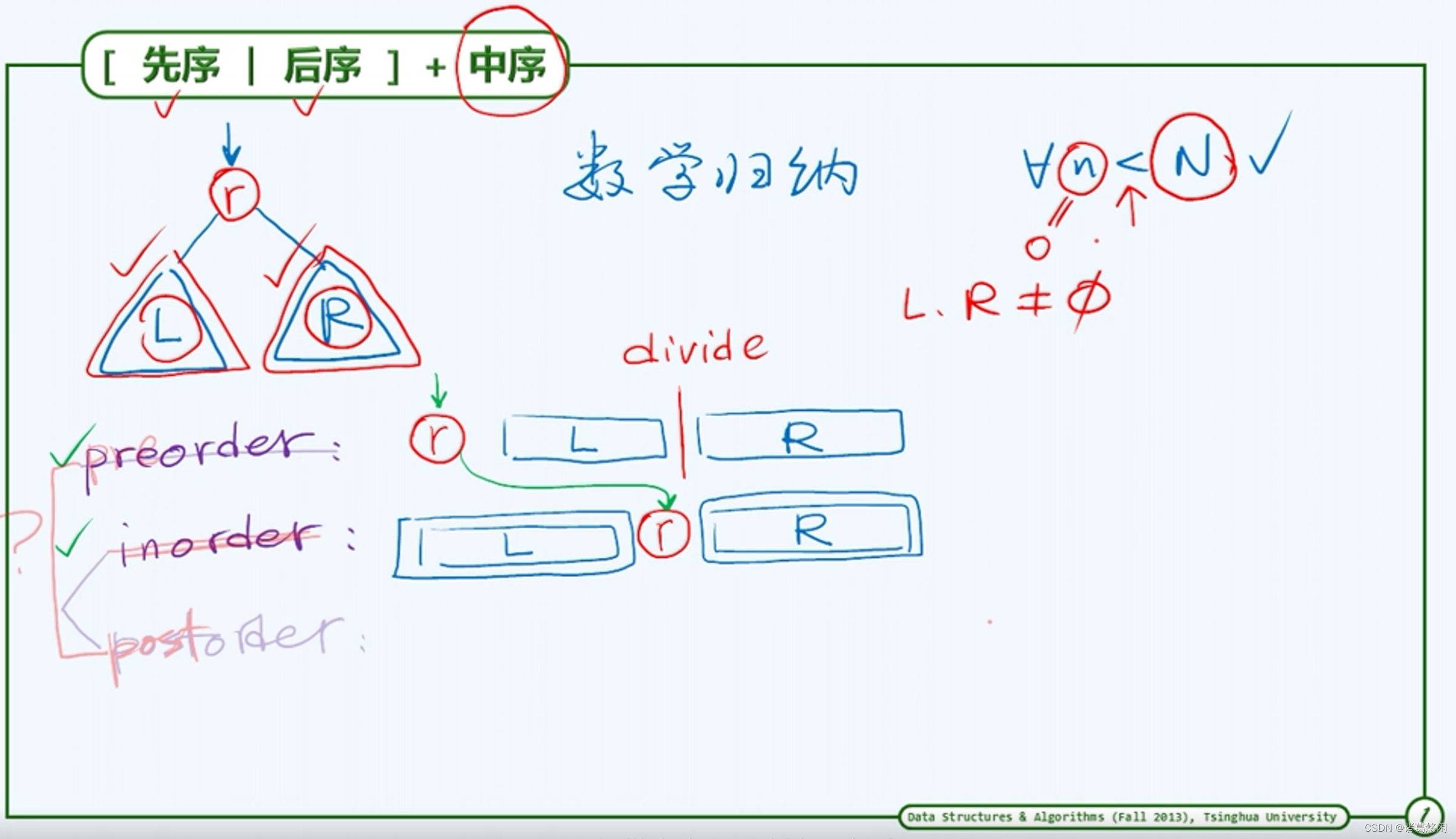
对于上述结论做证明,为此需要做数学归纳
假设对于规模小于N地所有二叉树这个规律都是成立的,接下来考虑规模恰好为N的二叉树。
不失一般性,可以将二叉树画成上图所示的样子。
先序遍历序列:r L R
中序遍历序列:L r R
因此根据先序遍历可以明确树根节点是谁,进而可以在中序遍历序列中对这个节点进行定位。这个定位非常重要,它使我们得以确认左子树所对应的中序遍历子序列,以及右子树所对应的中序遍历子序列。也就是说我们可以知道左子树和右子树分别是由哪些节点组成。因此只要这两个遍历序列是合法的,反过来在先序遍历序列中就可以很容易地将左子树和右子树所对应地遍历子序列切分开。
~
这样成功地将原来全树地重构问题,化解为两棵子树地重构问题。不难看出,这两棵子树在规模上都符合归纳假设,也就是它们都严格地小于N,因此根据归纳假设无论是左子树还是右子树的确都可以如此重构出来。
注意:无论是左子树还是右子树都有可能是空树,这种情况下树的规模应该是0。
不借助中序遍历序列,而只凭借先序和后序遍历序列,是否也能保证完成对左右子树地正确切分呢?答案是不能保证的。
原因是无论L 还是R都有可能是空树,比如右子树是空的,那么它对应的遍历:
先序遍历序列 r L
后序遍历序列 L r
反过来若左子树是空的,那么它对应的遍历:
先序遍历序列 r R
后序遍历序列 R r
可以看到这里出现了歧义,我们无法根据先序遍历序列以及后序遍历序列来区分在这种情况下,除去根节点之后的部分究竟是左子树还是右子树。
3. [先序 + 后序 ] x 真
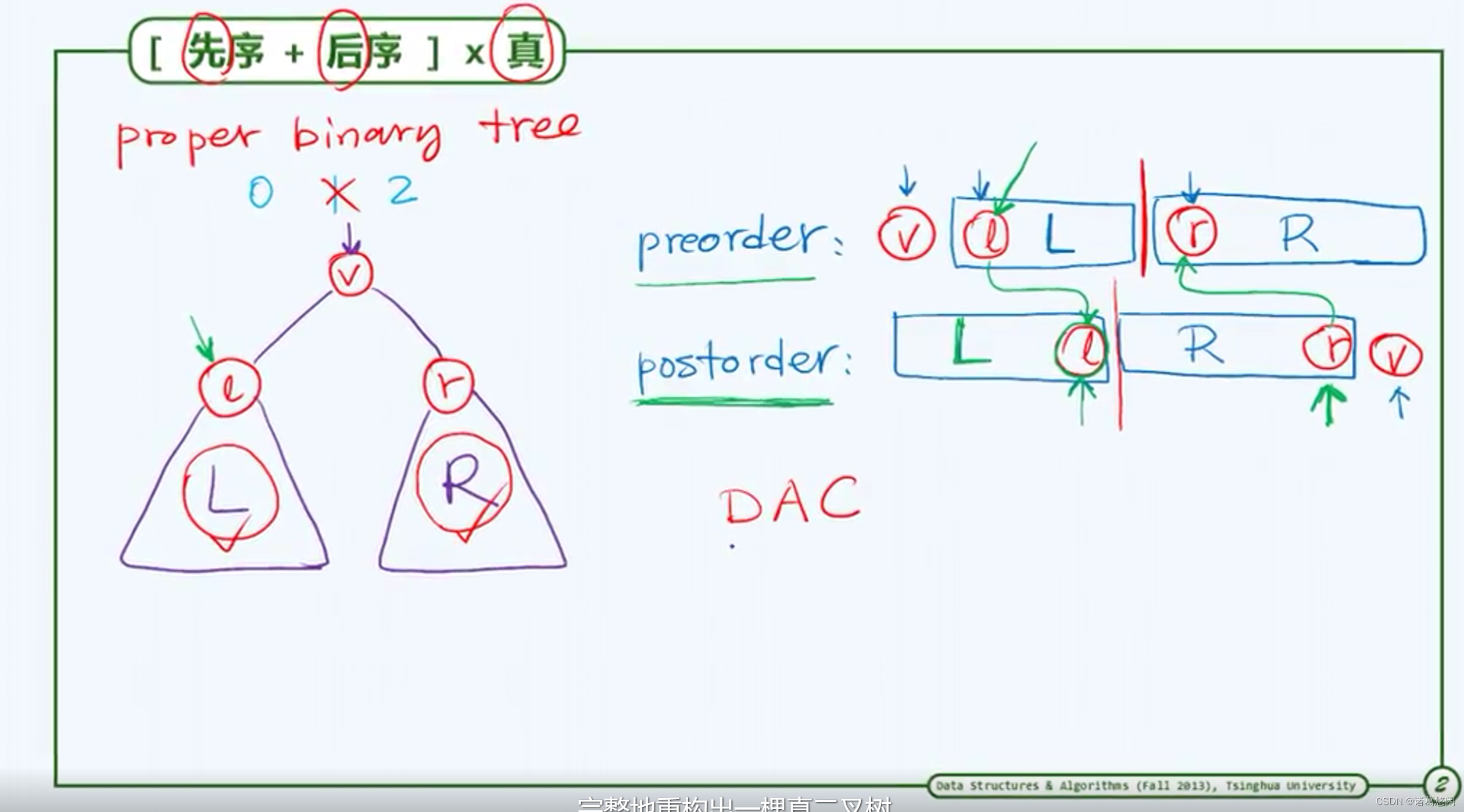
由先序和后序遍历序列的确也可以还原树的整体结构。比如对于所谓的真二叉树就是这样。
所谓的真二叉树,其中每个节点的度数都必须是偶数,确切说是除了0就是2度,而1度节点是严格禁止的。因此非退化的真二叉树模式无非如上图。注意,此时的左子树和右子树要么同时为空要么同时非空,前一种情况显而易见,因此不妨假设他们都存在。于是这棵树的遍历先序遍历序列和后序遍历序列如下。
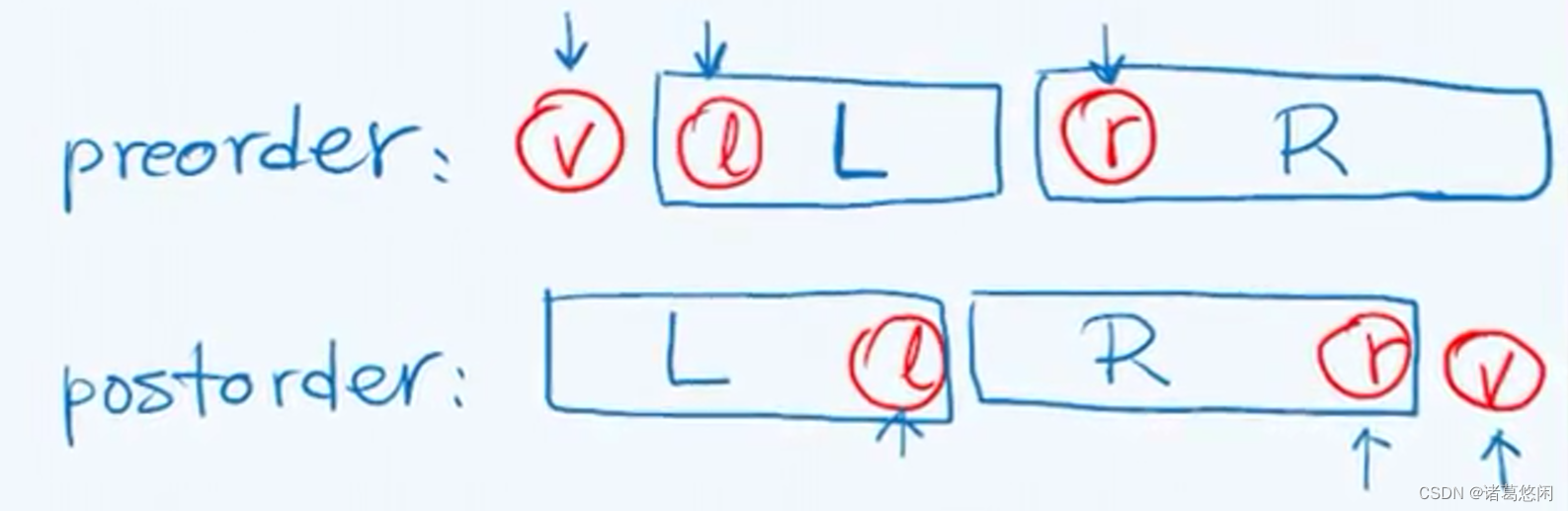
左子树的树根节点 l 在先序遍历序列中必然名列第二,位置是确定的,因此反过来,在任何给定的先序遍历序列中都可以便捷地找到它,进而在后序遍历序列中对它进行定位。这个节点在它所属地这棵子树地后序遍历子序列中必然垫后。这就意味着可以明确地界定左右子树范围。即左子树由哪些节点构成,右子树由哪些节点构成都是可以确定的。当然对称的,在后序遍历序列中,右子树的树根位置也是确定的,因此通过右子树的树根节点依然可以反过来在先序遍历序列中进行定位,而且同样地可以确定,左右子树地切分位置。
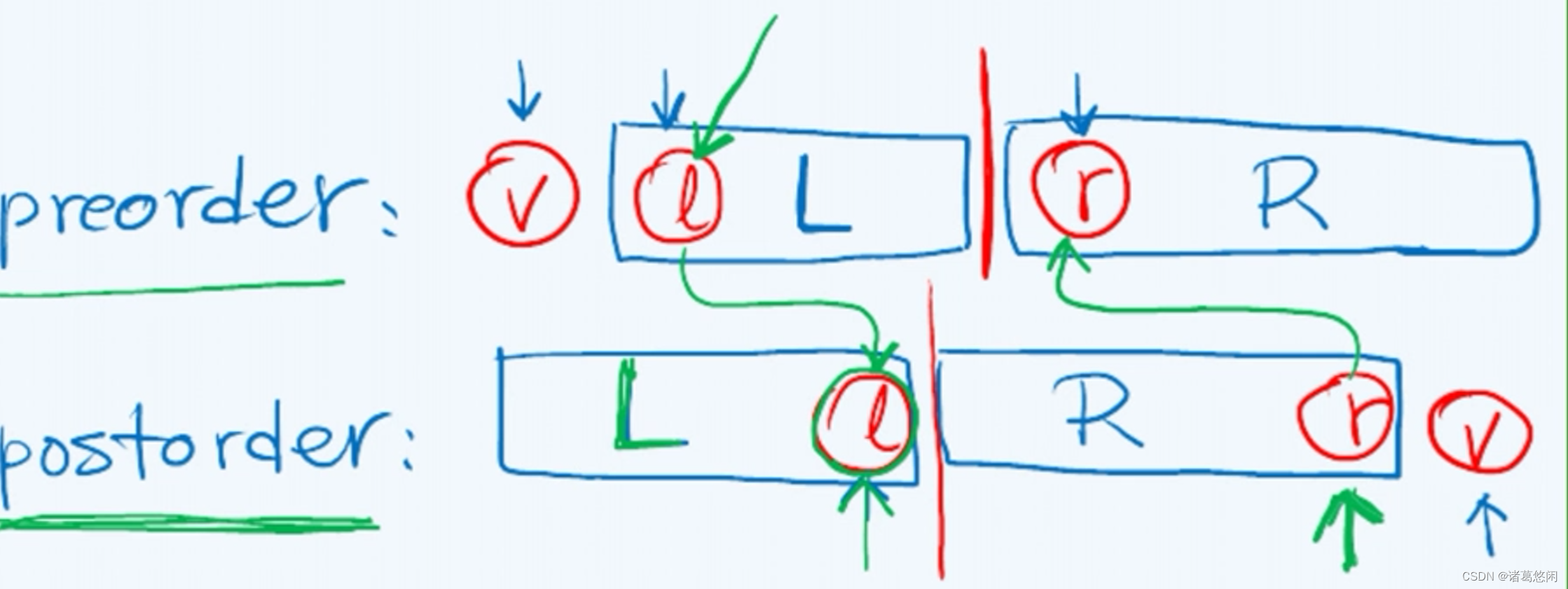
通过上述描述确实可以进行分而治之,从而通过递归的形式,完整地重构出一棵真二叉树。



)





)




)
,渲染100邀请码1a12)



