有了上篇文章的基础,先序和后序的线索化逻辑一样。
代码如下:
void preOrderThreadTree(TreeNode* T,TreeNode** pre) {if (T == NULL) {;}else {//printf("%c ", T->val);if (T->lchild == NULL) {T->ltag = 1;T->lchild = *pre;}if (*pre != NULL && (*pre)->rchild == NULL) {(*pre)->rtag = 1;(*pre)->rchild = T;}*pre = T;TreeNode* right = T->rchild;if (T->ltag != 1) {preOrderThreadTree(T->lchild, pre);}if (T->rtag != 1) {preOrderThreadTree(right, pre);}}
}
void postOrderThreadTree(TreeNode* T, TreeNode** pre) {if (T == NULL) {}else {postOrderThreadTree(T->lchild, pre);postOrderThreadTree(T->rchild, pre);if (T->lchild == NULL) {T->ltag = 1;T->lchild = *pre;}if (*pre != NULL && (*pre)->rchild == NULL) {(*pre)->rtag = 1;(*pre)->rchild = T;}*pre = T;}
}就是调整递归函数的顺序,就可以实现先序和后序的线索化,但是有一点需要注意,在先序遍历中,因为我们线索化之后会改变节点的左右孩子。举个例子:
T的左孩子为空,所以T指向自己的前驱*pre,然后执行 preOrderThreadTree(T->lchild, pre);,但是此时的 T->lchild 是已经改变过的而不是NULL,所以如果进入递归,函数会崩溃,T不能正常遍历。所以,当T->ltag等于1时,就不进入递归。
同样,当树即将遍历完时,如果没有考虑到树节点右孩子的改变,就也可能出现死递归的情况。
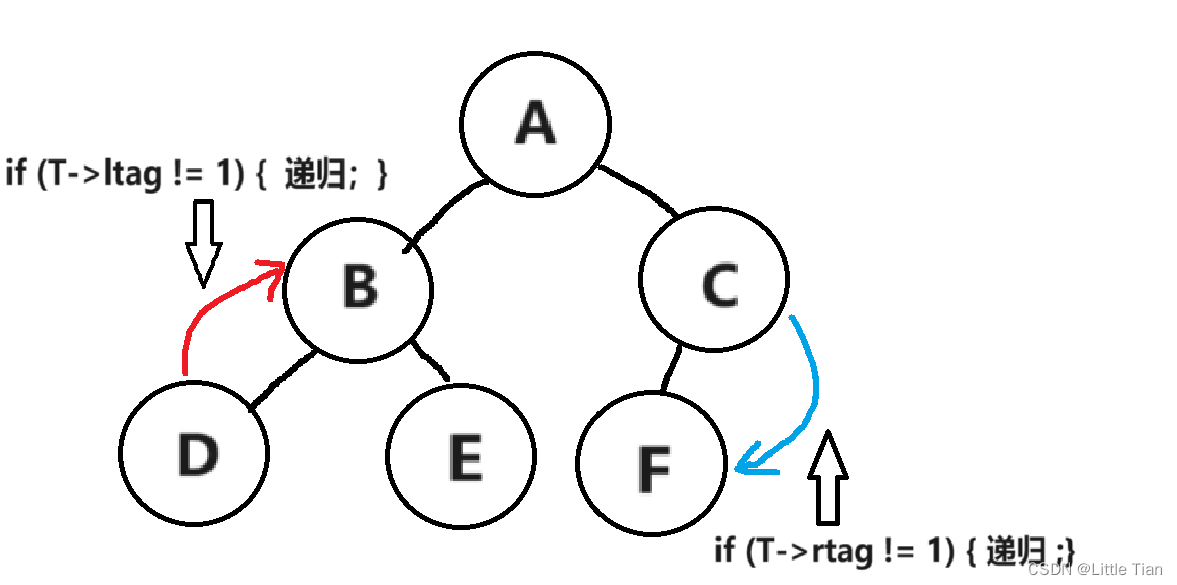
如图所示,先序遍历顺序;A B D E C F。这两个条件分别保护了在左右孩子改变的情况下可以正常进行递归的,否则就会回到前驱节点造成死递归。
那么为什么后序没有这样的问题,仔细观察会发现,后序遍历,递归操作在线索化之前,也就是说在改变左右孩子之前就已经遍历到目标节点,而先序的问题在于需要靠没有改变的左右节点遍历,但是中途有改变左右孩子的操作,所以遍历可能会出现问题。
接下来就是线索二叉树的遍历:
首先是先序线索二叉树的先序线索遍历:
TreeNode* GetNext(TreeNode* node) {if (node->ltag !=1) {node = node->lchild;}else {node = node->rchild;}return node;
}
int main() {char array[15] = "ABD##E##CF###";int index = 0;TreeNode* pre = NULL;TreeNode* T;MyTreeCreat(&T, array, &index);preOrderThreadTree(T,&pre);pre->rtag = 1;pre->rchild = NULL;for (TreeNode* node = T; node != NULL; node = GetNext(node)) {printf("%c ", node->val);}return 0;
}首先输入的是根节点,因为先序遍历是 根->左孩子->右孩子,所以只要 node->ltag !=1,就说明有左孩子,先序顺序根节点的下一个就是左孩子,如果没有左孩子,就指向右孩子,无论右孩子是真存在,还是不存在,都指向的是先序遍历的后继,所以,这就是先序遍历线索树。遍历主体是for循环。
接下来是后序线索二叉树的后序遍历:
void postOrderTraversal(PostThreadNode* root) {if (root == NULL) return;// 找到后序遍历的第一个节点PostThreadNode* cur = root;while (cur->left || cur->right) {if (cur->left) {cur = cur->left;} else if (cur->right) {cur = cur->right;}}// 遍历while (cur != NULL) {printf("%c ", cur->data);// 通过线索找到后继节点if (cur->right && (cur->right->left == cur || cur->right->right == cur)) {cur = cur->right;} else {cur = cur->successor;}}
}很抱歉我没有完全用之前的方法搞懂如何进行后序线索树的后序遍历,这是我在网上找到的示例代码。
这就是文章的全部内容了,希望对你有所帮助,如有错误欢迎指出。
)








demo)
)

—Vue + ECharts:流量数据可视化的强大组合)

使用细节3)
)

 FPGA通过ICAP原语读取芯片IDCODE实现方法)

