超简单白话文机器学习 - 逐步回归Lasso,Ridge正则化（含算法讲解，公式全解，手写代码实现，调包实现）

1. 提高泛化能力

1.1 概念

正则化是一种在机器学习和统计建模中用于防止过拟合的技术。过拟合是指模型在训练数据上表现很好，但在未见过的测试数据或新数据上表现不佳。正则化通过在损失函数（如最小二乘误差）中添加一个惩罚项，限制模型参数的复杂度，使得模型在训练数据和测试数据上都能表现良好。

1.2 为什么需要提高泛化能力

一个高大上的名词正则化，看的人一头雾水；了解正则化之前，我们需要明白为什么我们需要正则化。

下图是一张模型最终拟合出的三种不同效果：

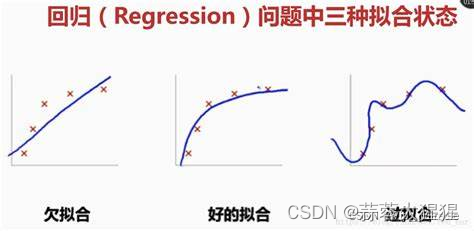
图一我们可以看出样本数据与最终拟合直线相差甚远，这叫做欠拟合，字面意思就是有些欠缺；

图二就是一个很好的拟合直线了，即使有一些噪音，但也无关轻重，这一类状态也是在测试集中预测效果最好的，也就是泛化能力最强。

图三就是过拟合，就像字面意思一般，拟合过头了，训练数据完全与模型贴合。我们训练模型的最终目的是预测，这一类模型使用测试集预测往往效果很不好。

重点来了，为了防止过拟合，我们就有了正则化。

2. 逐步回归

正则化不是唯一降低模型过拟合的方法。

逐步回归(Stepwise regression)是一种变量选择方法，用于从大量自变量中选择出对因变量最有影响的几个，从而简化回归模型，本段落着重叙述前向逐步回归。

2.1 前向逐步回归的步骤

逐步回归的基本思想是通过剔除变量中不太重要又和其他变量高度相关的变量，降低多重共线性程度。将变量逐个引入模型，每引入一个解释变量后都要进行F检验，并对已经选入的解释变量逐个进行t检验，当原来引入的解释变量由于后面解释变量的引入变得不再显著时，则将其删除，以确保每次引入新的变量之前回归方程中只包含显著性变量。这是一个反复的过程，直到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止，以保证最后所得到的解释变量集是最优的。

总结前向逐步回归的过程：

1. 初始化模型：

-从一个空模型开始，即模型中不包含任何自变量。

2. 选择变量：

-计算每个自变量和因变量之间的简单线性回归，并选择对因变量解释能力最强的那个变量加入模型。即选择P值最小且小于阈值的变量加入模型。

3. 更新模型：

-在已有的模型基础上，尝试加入新的自变量，并计算新的回归模型。

-比较加入新变量后的模型与原模型，根据统计准则判断是否保留。

4. 重复步骤2&3:

-不断重复上述过程，直到没有新的变量可以显著提高模型的解释能力。

2.2 如何选择变量以及更新模型

我们一般使用的P值检验去判断变量是否选择以及保留：

在选择变量中，我们对于每个变量去拟合简单线性模型，判断P值最小者去选择；

加入到模型后，重新拟合新的线性方差，若新加入的变量P值小与显著性水平，则保留该变量并继续；否则不加入这个新的变量。

P值计算步骤：

1. 拟合回归模型：

-使用最小二乘法拟合线性回归模型，计算回归系数和截距项。

2. 计算标准误差：

-标准误差反映了回归系数的不确定性，是回归系数的估计标准误差。

3. 计算t统计量：

-t统计量等于回归系数除以其标准误差。

4. 计算P值：

-根据t统计量和自由度，使用t分布计算P值。

2.3 手写代码实现

import statsmodels.api as sm
import pandas as pd# 假设 df 是包含所有变量的数据框，y 是因变量，X 是自变量
y = df['target']
X = df.drop('target', axis=1)def forward_selection(data, response, threshold_in=0.05):initial_features = []remaining_features = list(data.columns)while remaining_features:scores_with_candidates = []for candidate in remaining_features:model = sm.OLS(response, sm.add_constant(pd.DataFrame(data[initial_features + [candidate]]))).fit()p_value = model.pvalues[candidate]scores_with_candidates.append((p_value, candidate))scores_with_candidates.sort()best_p_value, best_candidate = scores_with_candidates.pop(0)if best_p_value < threshold_in:initial_features.append(best_candidate)remaining_features.remove(best_candidate)else:breakreturn initial_featuresselected_features = forward_selection(X, y)
print("Selected features: ", selected_features)

2.4 逐步回归的优点与局限性

2.4.1 优点

1. 简化模型：
- 逐步回归通过自动选择最重要的变量，可以简化模型，减少冗余变量，提高模型的可解释性。

2. 减少过拟合：
- 通过去除不显著的变量，逐步回归可以减少模型的复杂性，从而降低过拟合的风险。

3. 计算效率高：
- 相较于所有可能的子集回归，逐步回归计算效率更高，适用于包含大量变量的高维数据。

4. 自动化过程：
- 逐步回归的自动化过程使得变量选择相对简单，不需要手动挑选变量，节省时间和精力。

2.4.2 局限性

1. 忽略变量间的交互作用：
- 逐步回归通常忽略变量间的交互作用，可能会遗漏一些对因变量有重要影响的变量组合。

2. 多重共线性问题：
- 在存在多重共线性的情况下，逐步回归可能选择不稳定的变量，导致模型不稳定。

3. 偏差问题：
- 逐步回归的选择过程可能引入偏差，特别是在样本量较小的情况下，选择结果可能不稳定。

4. 过于依赖统计准则：
- 逐步回归过于依赖于统计准则（如p值、AIC、BIC等），可能忽视了业务逻辑和实际意义。

2.5 应用前景

1. 经济和金融分析：
- 在经济和金融数据中，逐步回归可以用于选择重要的经济指标和金融变量，建立预测模型。

2. 医学研究：
- 在医学研究中，逐步回归可以用于从大量潜在的风险因素中筛选出与疾病相关的主要因素，帮助诊断和治疗。

3. 市场营销：
- 在市场营销中，逐步回归可以用于分析影响消费者行为的关键因素，优化营销策略。

4. 环境科学：
- 在环境科学中，逐步回归可以用于分析环境数据，识别对环境变化最重要的因素。

5. 社会科学：
- 在社会科学研究中，逐步回归可以用于分析社会调查数据，找出影响社会现象的关键因素。

3. 正则化

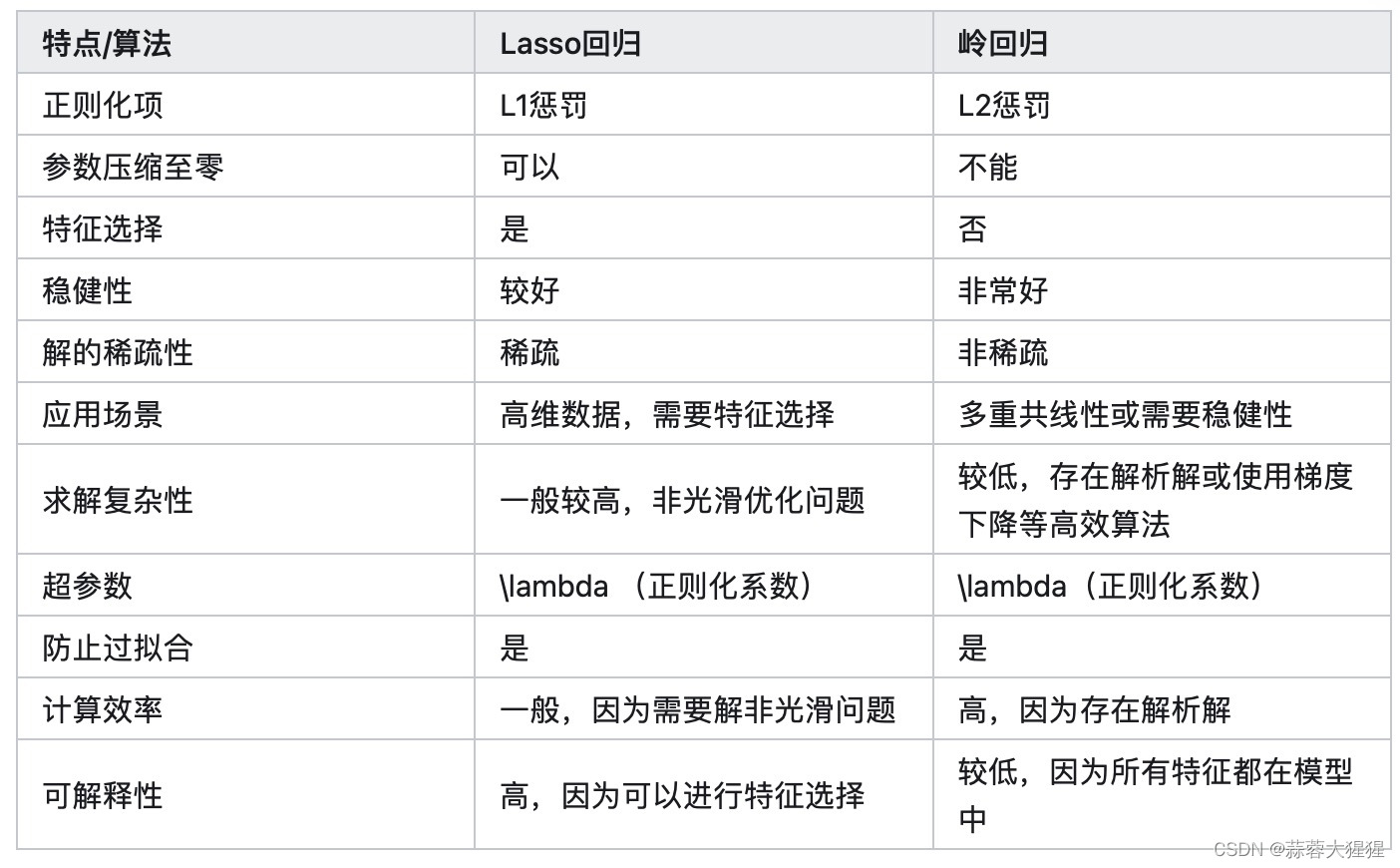
正则化是机器学习中防止模型过拟合的重要技术，通过对模型复杂度施加惩罚来提高模型的泛化能力。常见的算法有L1正则化(Lasso)，L2正则化(Ridge)。

3.1 Lasso

3.1.1 概述

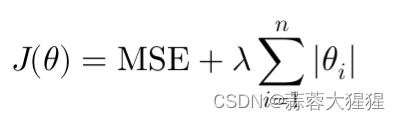
Lasso通过在损失函数中加入权重系数的绝对值的和来约束模型。

它的特点在于会讲一些权重系数缩减为零，从而实现特征选择。

其中正则化参数一般通过交叉验证进行选择，提高模型的性能与泛化能力。

3.1.2 Lasso程序实现

from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error# 假设 X 是自变量，y 是因变量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)lasso = Lasso(alpha=1.0)  # alpha 是正则化参数λ
lasso.fit(X_train, y_train)
y_pred = lasso.predict(X_test)
mse = mean_squared_error(y_test, y_pred)print("Lasso MSE:", mse)
print("Coefficients:", lasso.coef_)

3.2 Ridge

3.2.1 概述

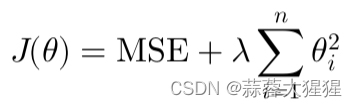
与Lasso不同的是，这里所加入的权重系数是平方和的形式进行约束。

特别适用于处理多重共线性问题，防止模型权重过大，提供更加稳定的解。但相反，Ridge不会将权重系数缩减为零，因此无法进行特征选择。

3.2.2 Ridge程序实现

from sklearn.linear_model import Ridgeridge = Ridge(alpha=1.0)  # alpha 是正则化参数λ
ridge.fit(X_train, y_train)
y_pred = ridge.predict(X_test)
mse = mean_squared_error(y_test, y_pred)print("Ridge MSE:", mse)
print("Coefficients:", ridge.coef_)