Leecode热题100---114：二叉树展开为链表

题目：
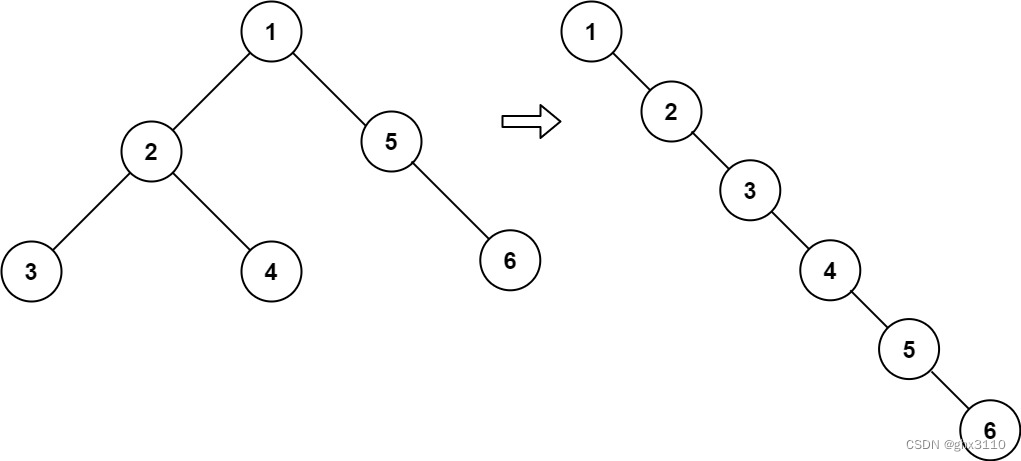
给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树先序遍历顺序相同。
在这里插入图片描述
思路：
(树的遍历) O(n)
从根节点遍历整颗树，对于当前节点：
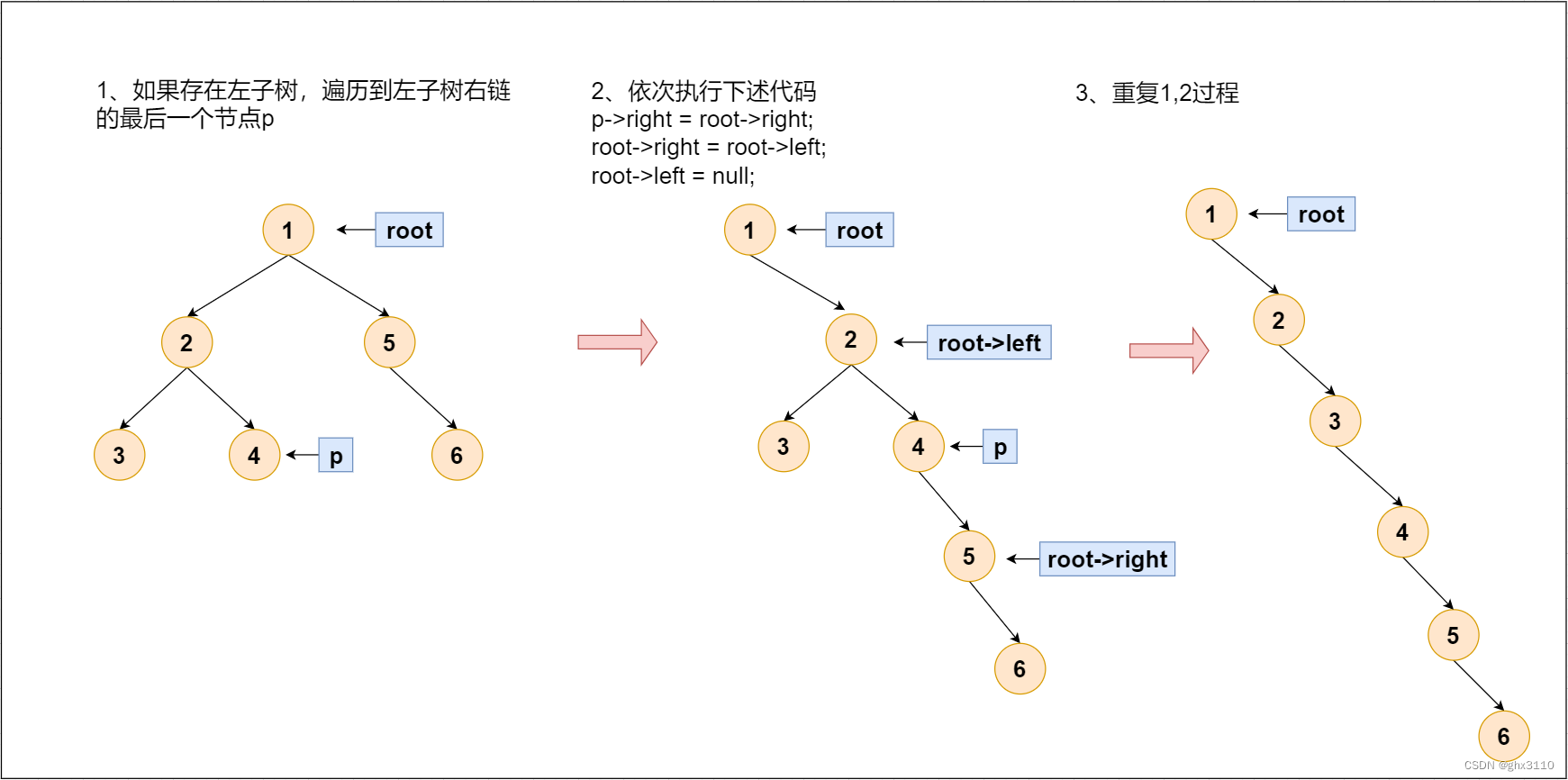
1、如果存在左子树，则将左子树插入当前节点右边。
2、否则，遍历至右子树
图示过程如下：

C++：

#include<iostream>
using namespace std;struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode();TreeNode(int x){val = x;left = right = nullptr;}TreeNode(int x,TreeNode *left,TreeNode *right){val = x;left = left;right = right;}
};class Solution
{
public:void flatten(TreeNode *root){TreeNode* p = root->left;if(p != nullptr){// 找到根左节点分支的最右节点while(p->right != nullptr){p = p->right;}p->right = root->right;root->right = root->left;root->left = nullptr;}root = root->right;}
};

Python：
解题思路：依次将每个节点的子节点进行操作。

class TreeNode:def __init__(self,val = 0,left = None, right = None):self.val = xself.left = leftself.right = rightclass Solution:def flatten(self,root):while root:if root.left:				# 左子树存在才进行操作sub_left = root.leftwhile sub_left.right:   # 左子树的右子树找到最深sub_left = sub_left.right# 将root的右子树挂到左子树的右子树的最深sub_left.right = root.rightroot.right = root.left	# 将root的左子树挂到右子树root.left = None		# 清空左子树root = root.right			# 继续下一个节点