超简单白话文机器学习 - 支持向量机SVM（含算法讲解，公式全解，手写代码实现，调包实现）

1. 支持向量机SVM

支持向量机，因其英文名为support vector machine，故一般简称SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

1.1 概述

支持向量机是一种线性分类器。

打住，可能有同学会问到什么是线性分类器。

这是线性模型的定义，通俗来讲就是对于一个样本而言，通过他的特征进行计算得出一个值大于或小于某个特定的数，进而他的标签可以通过这个数字进行区分，这就是线性可分。

如同上述的例子，若z大于等于0，则属于1类；反之为-1类。

线性模型如同它的名字一般，用一组线性方程(W，b），其中W为向量将数据进行切割。在二维平面上的形式为一条线，三维平面则是一个面。换言之，在进行分类的时候，遇到一个新的数据点x，将x代入f(x) 中，如果f(x)小于0则将x的类别赋为-1，如果f(x)大于0则将x的类别赋为1。

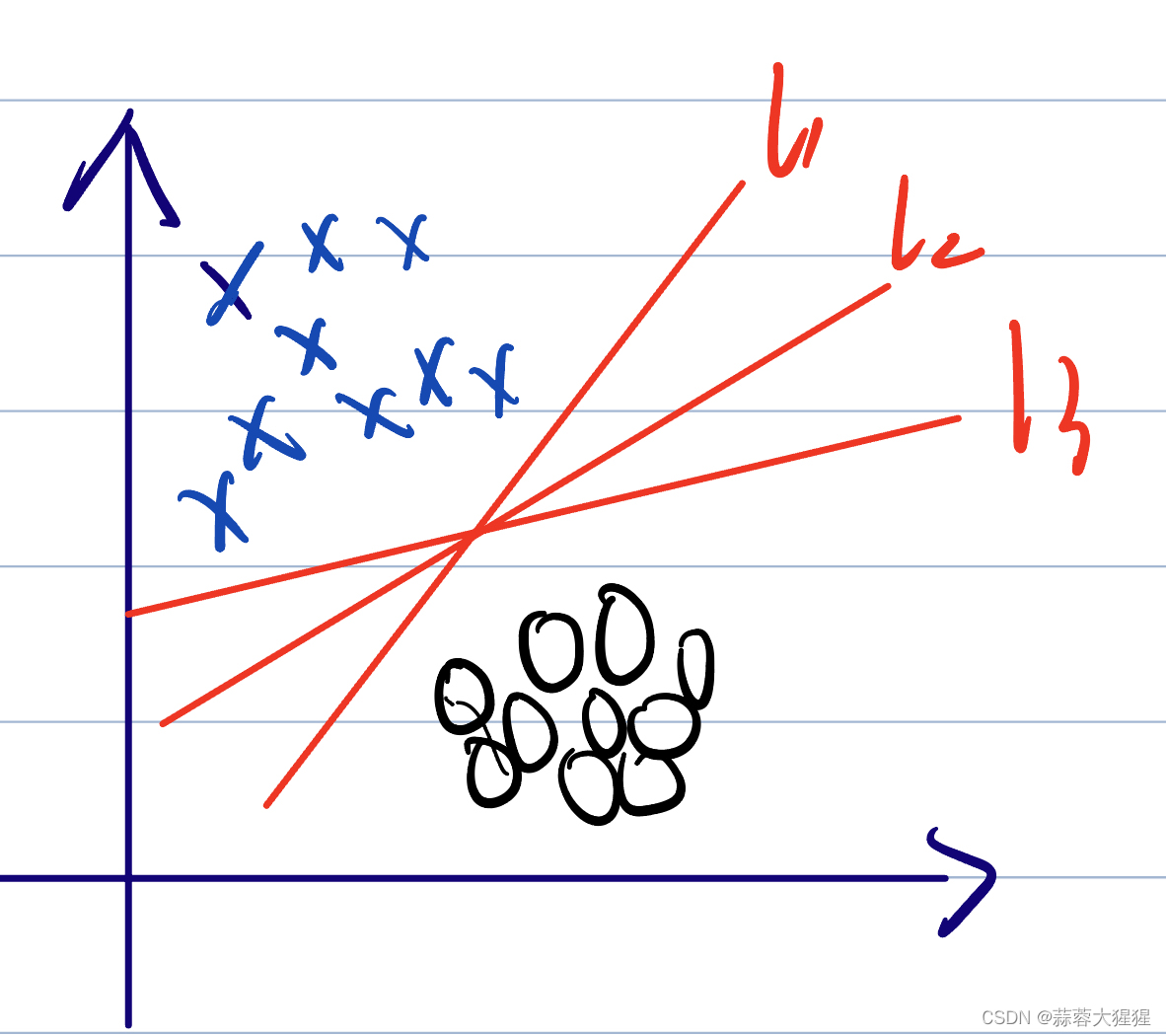
SVM的本质就是找到这样的一个超平面进行二分类，上图所示，构建了三条直线进行划分蓝色的叉和黑色的圆。但又产生了一个问题，这三条线L1,L2,L3都可以将数据进行切分，哪一条才是最好的，进行预测时最不容易出错的呢？

这就是SVM的核心：这条直线离直线两边的数据的间隔最大，寻找有着最大间隔的超平面。

1.2 算法详解

1.2.1 线性可分

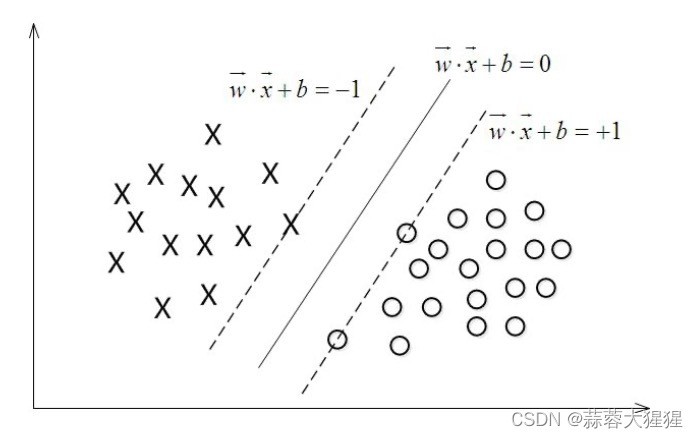
从SVM的角度，如图最中间的一条线就是最适合用来切分样本的。上下两条距离中间线函数距离为1的线，是w*x + b = 0函数缩放得到，在这两条线上的点被称之为支持向量。换个理解方式，支持向量就是距离超平面距离最近的数据，其他数据都需要大于或等于这个距离，这才是最佳切分方式。类似于领土的边疆，不能跨过边疆，理解了这个在后面的推导中就能理解什么是限制式了。这两个边疆之间的距离就是间隔，SVM的本质就是寻找最大间隔。

于是模型的预测方式也很简单，在进行分类的时候，遇到一个新的数据点x，将x代入f(x) 中，如果f(x)小于0则将x的类别赋为-1，如果f(x)大于0则将x的类别赋为1；反之也一样，代入函数中判断数值大小确定分类结果。

如何确定这个最佳的超平面呢？

首先我们需要明白这样的一个事实：

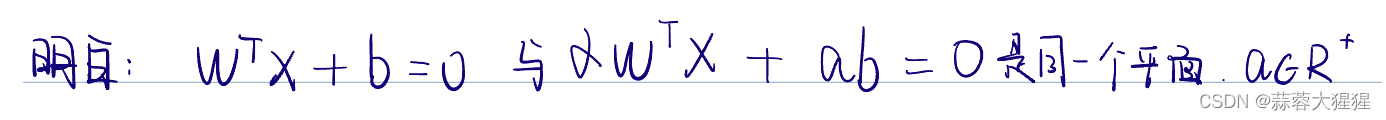
让我们开始推导，既然也找最大间隔，点到平面距离公式就派上用场了。

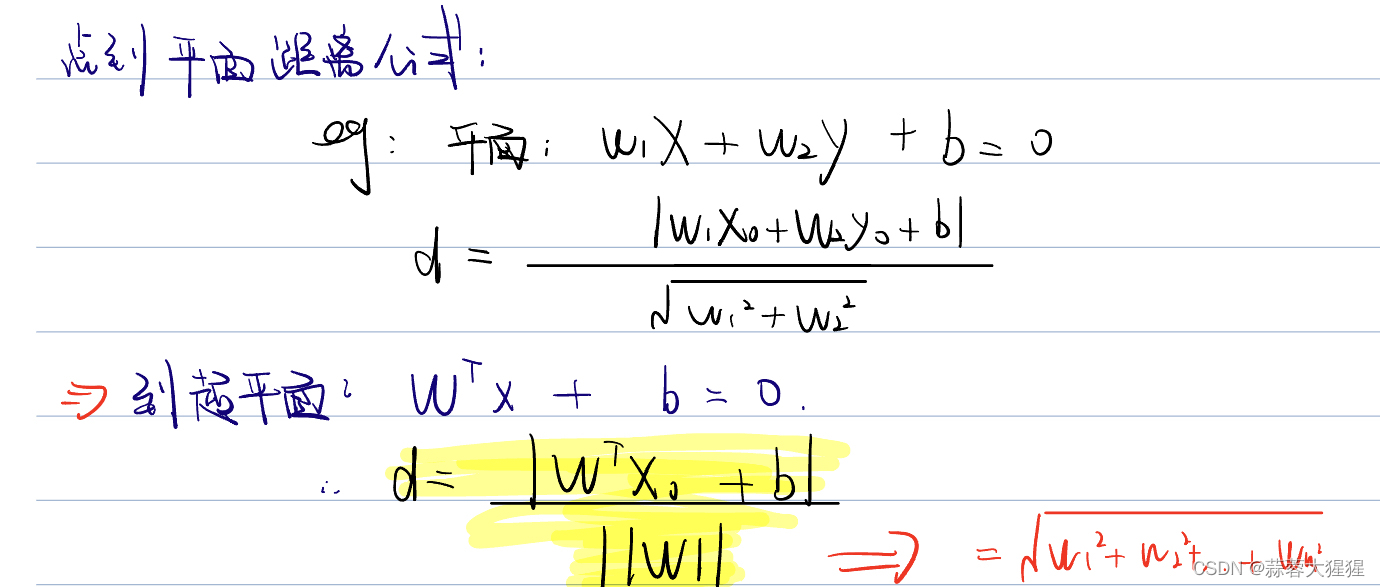
W也是一组向量，分母代表着W的内积。

上述我们说了，支持向量到超平面的函数距离需要为1，我们可以观察d的分子恰好也是函数距离的表达式，让我们使用一个阿尔法进行缩放

最后讲距离公式进行化简，代入1，得到距离公式为

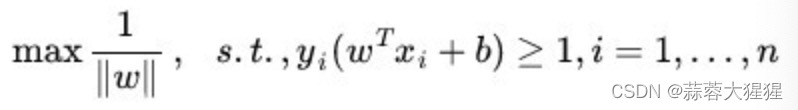
最大化一个分数意味着最小化它的分子，将式子进行转换得到：

1.2.2 线性不可分

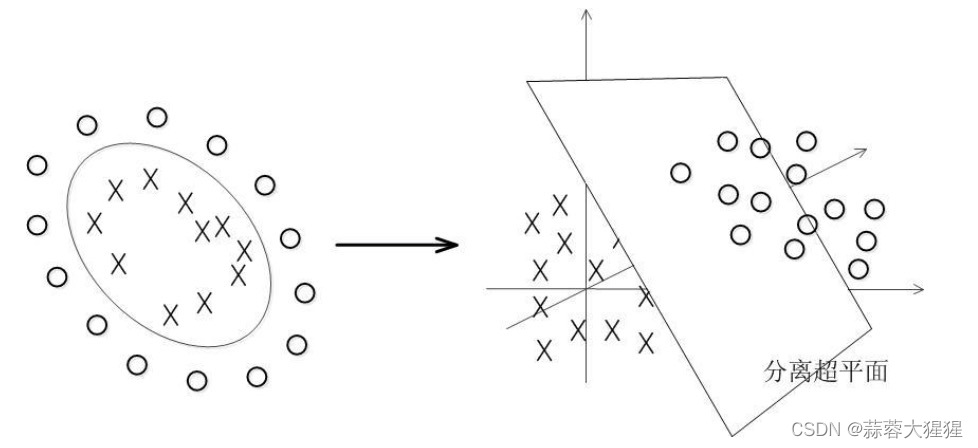
但现实生活中往往数据是线性不可分的，上图中可以看到一堆叉包围黑色的圆圈，用肉眼可见画一个圆圈就可以将数据进行划分，但根据上述的原则，只凭借一条直线是根本不可能将数据进行分割。这个时候我们需要引入一个松弛变量。松弛变量让边界线定的不那么死，但为了防止边界的过大，我们需要最小化。

注：原式系数变为1/2是因为在后续求导更好计算，系数大小对求极值没有影响。

在支持向量机中，我认为最具有创造性的一点就是将低纬度数据转换为高纬度。

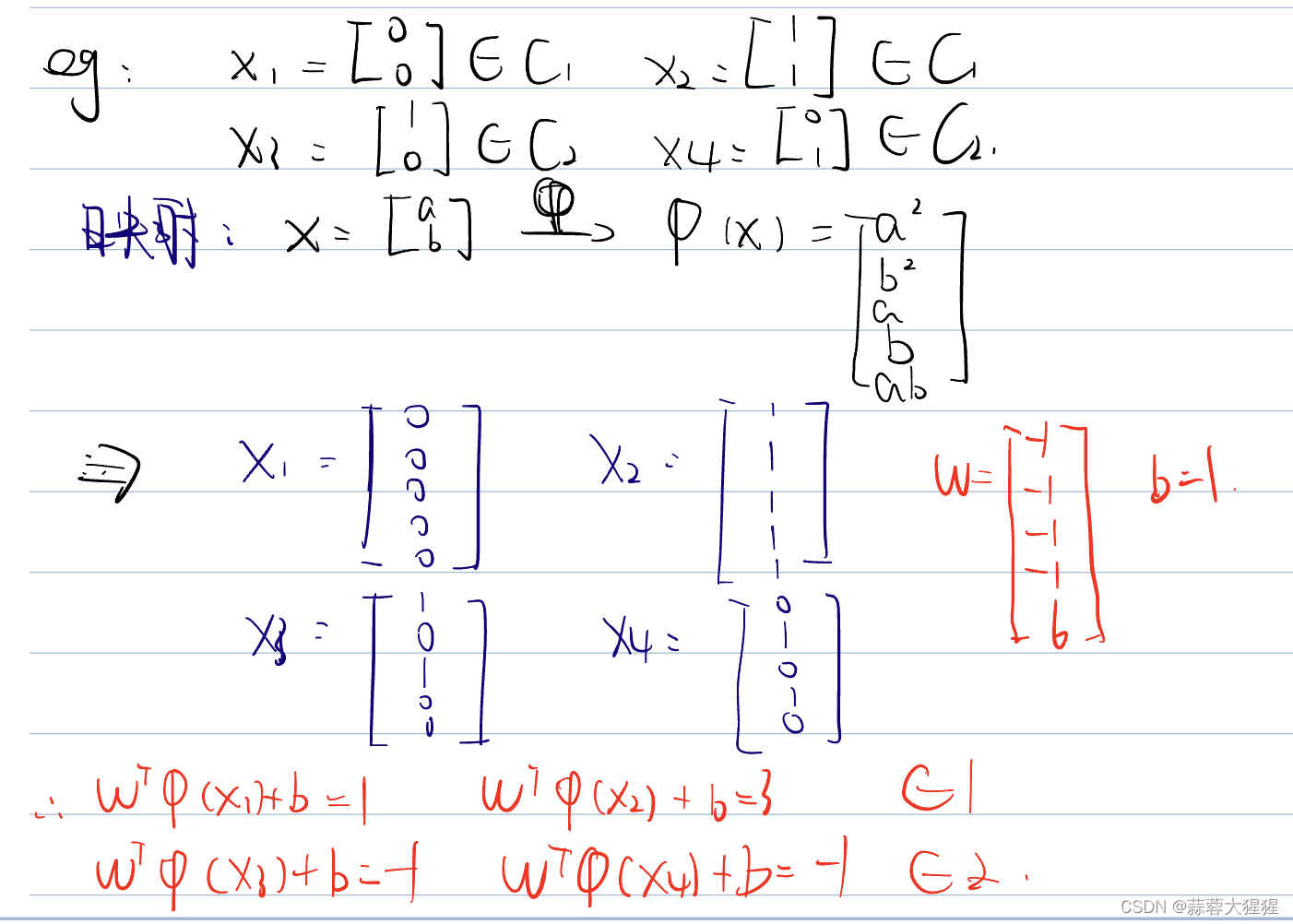
如果同学仍然觉得抽象可以动手做一做下面的这道例题，低维度数据转化为高维度数据划分：

而在我们遇到核函数之前，如果用原始的方法，那么在用线性学习器学习一个非线性关系，需要选择一个非线性特征集，并且将数据写成新的表达形式，这等价于应用一个固定的非线性映射，将数据映射到特征空间，在特征空间中使用线性学习器，因此，考虑的假设集是这种类型的函数：

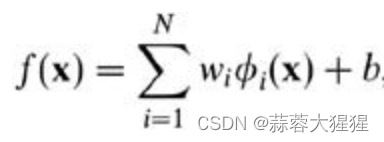
那么如何选择维度？

一千个读者心中有一千个哈姆雷特，SVM创造者认为：

既然是无限维度，怎样进行映射，这样计算量岂不是一个天文数字？

我们可以通过核函数进而解决这个问题。

核函数能简化映射空间中的内积运算——刚好“碰巧”的是，在我们的 SVM 里需要计算的地方数据向量总是以内积的形式出现的。

关于数学推导大家可以看看这篇文章：支持向量机通俗导论（理解SVM的三层境界）-CSDN博客

1.3 核函数

1. 线性核（Linear Kernel）：最简单的核函数，直接计算向量之间的内积，不适用于线性不可分问题：

2. 多项式核（Polynomial Kernel）：通过多项式函数映射到更高维度空间，d是多项式的阶数

3. 高斯核（Gaussian Radial Basis Function Kernel）:这是最常用的核函数，将输入映射到无穷维空间，其中sigma是方差(宽度系数).

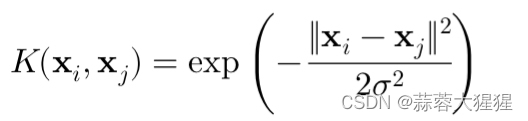
2. 手写代码实现

2.1 算法实现

import numpy as npclass SimpleSVM:def __init__(self, learning_rate=0.001, lambda_param=0.01, n_iters=1000):self.learning_rate = learning_rateself.lambda_param = lambda_paramself.n_iters = n_itersself.w = Noneself.b = Nonedef fit(self, X, y):n_samples, n_features = X.shapey_ = np.where(y <= 0, -1, 1)self.w = np.zeros(n_features)self.b = 0for _ in range(self.n_iters):for idx, x_i in enumerate(X):condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1if condition:self.w -= self.learning_rate * (2 * self.lambda_param * self.w)else:self.w -= self.learning_rate * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))self.b -= self.learning_rate * y_[idx]def predict(self, X):approx = np.dot(X, self.w) - self.breturn np.sign(approx)# 测试我们的SVM
if __name__ == "__main__":# 生成简单的数据from sklearn.datasets import make_blobsimport matplotlib.pyplot as pltX, y = make_blobs(n_samples=50, centers=2, random_state=42)y = np.where(y == 0, -1, 1)# 训练SVMclf = SimpleSVM()clf.fit(X, y)predictions = clf.predict(X)# 画出数据点和决策边界def visualize_svm():def get_hyperplane_value(x, w, b, offset):return (-w[0] * x + b + offset) / w[1]fig, ax = plt.subplots()plt.scatter(X[:, 0], X[:, 1], marker='o', c=y, s=25, edgecolor='k')x0_1 = np.amin(X[:, 0])x0_2 = np.amax(X[:, 0])x1_1 = get_hyperplane_value(x0_1, clf.w, clf.b, 0)x1_2 = get_hyperplane_value(x0_2, clf.w, clf.b, 0)x1_1_m = get_hyperplane_value(x0_1, clf.w, clf.b, -1)x1_2_m = get_hyperplane_value(x0_2, clf.w, clf.b, -1)x1_1_p = get_hyperplane_value(x0_1, clf.w, clf.b, 1)x1_2_p = get_hyperplane_value(x0_2, clf.w, clf.b, 1)ax.plot([x0_1, x0_2], [x1_1, x1_2], 'k')ax.plot([x0_1, x0_2], [x1_1_m, x1_2_m], 'k--')ax.plot([x0_1, x0_2], [x1_1_p, x1_2_p], 'k--')x1_min = np.amin(X[:, 1])x1_max = np.amax(X[:, 1])ax.set_ylim([x1_min - 3, x1_max + 3])plt.show()visualize_svm()

2.2 核函数实现

1. 线性核函数：

def linear_kernel(x1,x2):return np.dot(x1,x2)

2. 多项式核函数：

def polynomial_kernel(x1,x2,degree=3,coef0=1):return (np.dot(x1,x2) + coef0) ** degree

3. 高斯核函数：

def rbf(x1,x2,sigma=1.0):return np.exp(-np.linalg.norm(x1 - x2)**2 / (2 * (sigma ** 2)))

3. 调包实现

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt# 创建训练数据
X = np.array([[2, 3], [3, 4], [1, 1], [5, 6], [6, 5], [7, 8]])
y = np.array([1, 1, -1, -1, -1, 1])# 创建线性SVM模型
clf = svm.SVC(kernel='linear', C=1.0)# 训练模型
clf.fit(X, y)# 获取超平面参数
w = clf.coef_[0]
b = clf.intercept_[0]# 打印支持向量
print("Support vectors:", clf.support_vectors_)# 可视化结果
def plot_hyperplane(clf, X, y):plt.scatter(X[:, 0], X[:, 1], c=y, cmap='bwr', s=30)ax = plt.gca()xlim = ax.get_xlim()ylim = ax.get_ylim()# 创建网格以评估模型xx = np.linspace(xlim[0], xlim[1], 30)yy = np.linspace(ylim[0], ylim[1], 30)YY, XX = np.meshgrid(yy, xx)xy = np.vstack([XX.ravel(), YY.ravel()]).TZ = clf.decision_function(xy).reshape(XX.shape)# 画决策边界和边界ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,linestyles=['--', '-', '--'])ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,linewidth=1, facecolors='none', edgecolors='k')plt.show()plot_hyperplane(clf, X, y)