什么是ELK
ELK 并不是一个技术框架的名称，它其实是一个三位一体的技术名词，ELK 的每个字母都来自一个技术组件，分别是 Elasticsearch（简称 ES）、Logstash 和 Kibana。
三个技术组件是独立的，后两个被elastic公司收购，通常配合起来使用。
ELK的组成部分
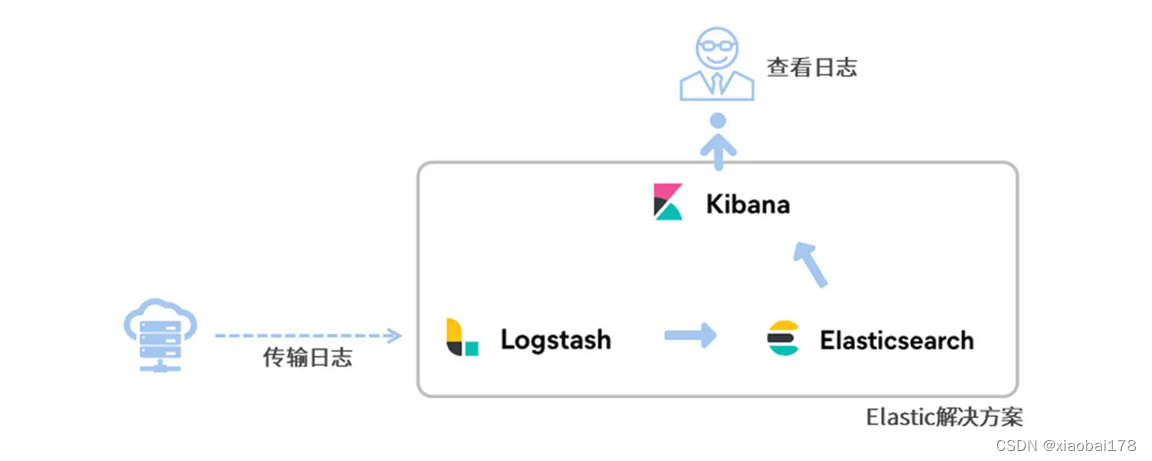
- Elasticsearch：是一个分布式的搜索和数据分析引擎。在整套方案中会收到来自 Logstash 的日志信息，并将这些日志信息集中存储起来，同时，Elasticserch 还对外提供了多种 RESTful 风格的接口，上层应用可以通过这些接口完成数据查找和分析的任务。
- Logstash：用于收集、过滤和转换日志数据，支持多种数据源和数据格式。
- Kibana：提供了一套 UI 界面，让我们可以对 Elasticsearch 中存储的数据进行查找，同时还提供丰富的图表和仪表盘功能。
部署方法
- 分别搭建并相互集成
- 直接下载已经集成了ELK的镜像
常用来做日志分析
日志的作用：
定位bug
功能报错的监控
了解用户的行为和使用习惯
安全监控
性能方案制定和性能优化
