【题目来源】
https://www.luogu.com.cn/problem/P3372

【题目描述】
如题，已知一个数列，你需要进行下面两种操作：
（1）将某区间每一个数加上 k。
（2）求出某区间每一个数的和。

【输入格式】
第一行包含两个整数 n,m，分别表示该数列数字的个数和操作的总个数。
第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。
接下来 m 行每行包含 3 或 4 个整数，表示一个操作，具体如下：
1 x y k：将区间 [x,y] 内每个数加上 k。
2 x y：输出区间 [x,y] 内每个数的和。

【输出格式】
输出包含若干行整数，即为所有操作 2 的结果。

【输入样例】
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4​​​​​​​

【输出样例】
11
8
20

【说明/提示】
对于 30% 的数据：n≤8，m≤10。
对于 70% 的数据：n≤10^3，m≤10^4。
对于 100% 的数据：1≤n,m≤10^5。
保证任意时刻数列中所有元素的绝对值之和 ≤10^18。

【算法分析】
● 本题其实就是线段树的模板题，这里用来练习分块。
● 分块是用线段树的分区思想改良的暴力法。代码比线段树简单。效率比普通暴力法高。分块适合求解 m=n=10^5 规模的问题。或 m*sqrt(n)≈10^7 的问题。其中，n 为元素个数，m 为操作次数。
● 分块操作的基本要素
（1）块的大小用 block 表示。通常，令 block=sqrt(n)。其中，n 为元素个数。
（2）块的数量用 cnt 表示。其计算公式为 cnt=(n+block-1)/block。或者，用如下更易理解的代码计算 cnt 的值。即：

int block=sqrt(n);
int cnt=n/block;
if(n % block) cnt++;

（3）块的左边界 le[] 及右边界 ri[]。
若用 le[i] 和 ri[i] 分别表示块 i 的第一个和最后一个元素的位置。则有：
le[1]=1, ri[1]=block;
le[2]=block+1, ri[2]=2*block;
……
le[i]=(i-1)*block+1, ri[i]=i*block;
……
（4）定义 pos[i] 为第 i 个元素所在的块：pos[i]=(i-1)/block+1。其中，block=sqrt(n)。
（5）定义 sum[i] 为第 i 块的区间和。

for(int i=1; i<=n; i++) sum[pos[i]]+=a[i];

（6）定义 add[i] 为第 i 块的增量，初始值为 0。
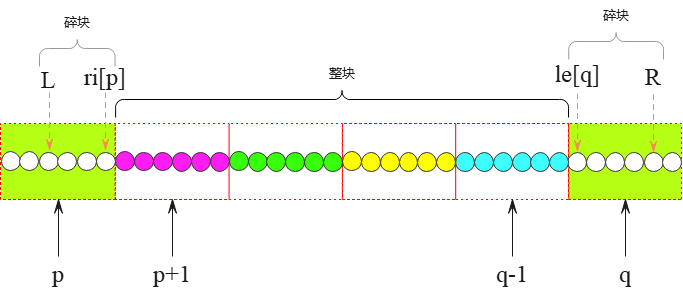
一般情况下，区间 [L,R] 跨越了多个块。
在被 [L,R] 完全包含的整块内，更新 add[i]=add[i]+d;
位于整块两头，不能被 [L,R] 完全包含的两个碎块，分别更新 sum(p)=sum(p)+(ri[p]-L+1)*d，sum(q)=sum(q)+(R-le[q]+1)*d。

【算法代码】

#include <bits/stdc++.h>
using namespace std;typedef long long LL;
const int maxn=1e5+5;LL a[maxn];
LL le[maxn],ri[maxn],pos[maxn];
LL sum[maxn],add[maxn];
int cnt;void build(int n) {int block=sqrt(n);int cnt=n/block;if(n%block) cnt++;for(int i=1; i<=cnt; i++) {le[i]=(i-1)*block+1;ri[i]=i*block;}ri[cnt]=n;for(int i=1; i<=n; i++) pos[i]=(i-1)/block+1;for(int i=1; i<=n; i++) sum[pos[i]]+=a[i];
}void update(int L,int R,int d) { //section updateint p=pos[L],q=pos[R];if(p==q) {for(int i=L; i<=R; i++) a[i]+=d;sum[p]+=(R-L+1)*d;} else {for(int i=p+1; i<=q-1; i++) add[i]+=d;for(int i=L; i<=ri[p]; i++) a[i]+=d;sum[p]+=(ri[p]-L+1)*d;for(int i=le[q]; i<=R; i++) a[i]+=d;sum[q]+=(R-le[q]+1)*d;}
}LL query(int L,int R) { //LLint p=pos[L],q=pos[R];LL ans=0; //LLif(p==q) {for(int i=L; i<=R; i++) ans+=a[i];ans+=add[p]*(R-L+1);} else {for(int i=p+1; i<=q-1; i++) ans+=sum[i]+add[i]*(ri[i]-le[i]+1);for(int i=L; i<=ri[p]; i++) ans+=a[i];ans+=add[p]*(ri[p]-L+1);for(int i=le[q]; i<=R; i++) ans+=a[i];ans+=add[q]*(R-le[q]+1);}return ans;
}int main() {int n,m;cin>>n>>m;for(int i=1; i<=n; i++) cin>>a[i];build(n);while(m--) {int op,a,b,c;cin>>op>>a>>b;if(op==1) {cin>>c;update(a,b,c);} else cout<<query(a,b)<<endl;}return 0;
}/*
in:
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4out:
11
8
20
*/

【参考文献】
https://blog.csdn.net/m0_52398496/article/details/123233908
https://blog.csdn.net/weixin_45539557/article/details/116461380
https://blog.csdn.net/wzh1378008099/article/details/89243459