💓博主CSDN主页:杭电码农-NEO💓
⏩专栏分类:高阶数据结构专栏⏪
🚚代码仓库:NEO的学习日记🚚
🌹关注我🫵带你学习更多Go语言知识
🔝🔝

高阶数据结构
- 1. 前言
- 2. 图的遍历
- 3. 图的广度优先遍历
- 4. 图的深度优先遍历
- 5. 图的最小生成树
- 6. Kruskal算法讲解
- 7. prim算法讲解
- 8. 总结以及拓展
1. 前言
如果你还不知道什么是图论,以及关于图的存储结构和一些专有名词, 请先阅读这篇文章: 初识图论.
本章重点:
本篇文章着重讲解图的两种遍历方式: 深度优先遍历和广度优先遍历. 并会模拟实现这两种遍历方法. 其次,会讲解关于图的最小生成树的概念,以及关于最小生成树的两个算法: Kruskal算法和Prim算法
2. 图的遍历
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶点仅被遍历一次。
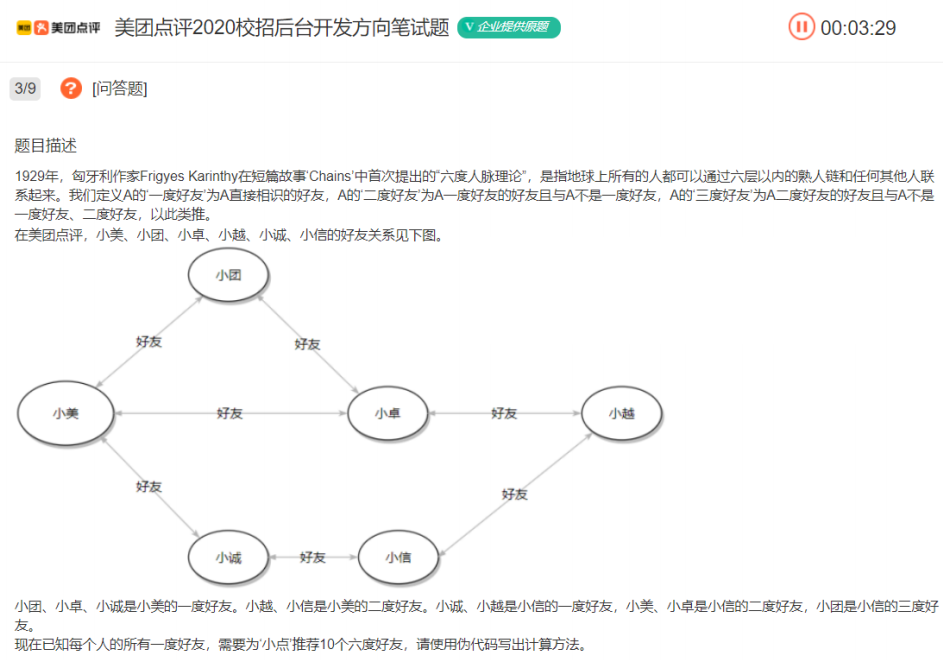
这道面试题就是典型的图论的遍历
3. 图的广度优先遍历
正如其名, 广度优先遍历就是先遍历完一个顶点的所有相邻顶点
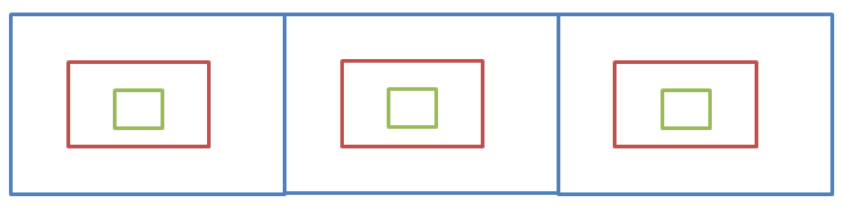
比如现在要找东西,假设有三个抽屉,东西在那个抽屉不清楚,现在要将其找到,广度优先遍历的做法是:
- 先将三个抽屉打开,在最外层找一遍
- 将每个抽屉中红色的盒子打开,再找一遍
- 将红色盒子中绿色盒子打开,再找一遍直到找完所有的盒子
注意:每个盒子只能找一次,不能重复找
具体到一个图中就是这样的:
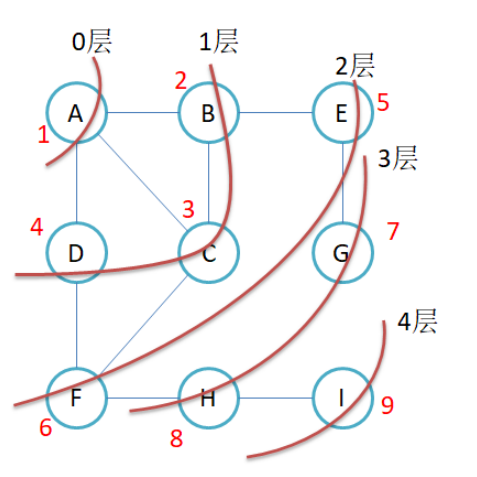
广度优先遍历看似很简单, 对于顶点A来说, 先走B,C,D. 然后再看B顶点, 走A,C,E, 但是A和C已经走过了,所以不能再此将它们算进去. 做法很简单, 使用一个队列和一个数组, 数组用来存储一个顶点是否已经入过队列了. 对于队列而言, 它的功能相信我不说大家也能明白: 最开始只有A在队列中, A出队, BCD入队, B出队, AC不用入队, 只入E. C出队…
话不多说,直接上代码:
void BFS(const V& src) //图的广度优先遍历
{size_t srci = _index[src];//找到值src对应在数组中的下标queue<int> q;vector<bool> check(_vertex.size(), false); //用来标记哪些元素已经入过队列了q.push(srci);check[srci] = true;while (!q.empty()){int front = q.front();cout << front << ": " << _vertex[front] << endl;q.pop();//把这个顶点的朋友带入队列,并更新check数组for (int i = 0; i < _vertex.size(); i++){//_edge[front][i]代表front->i是否有边,数组值不等于MAX_W就代表它们之间直接相连if (_edge[front][i] != MAX_W && check[i] == false){check[i] = true;q.push(i);}}}
}
注意,此函数是在graph类中实现的成员函数, 其中使用到了成员变量
4. 图的深度优先遍历
正如其名, 深度优先遍历就是先一条路走到底
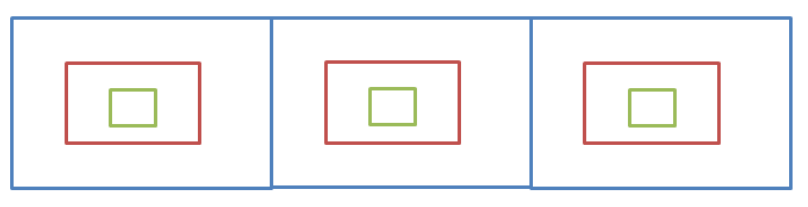
比如现在要找东西,假设有三个抽屉,东西在那个抽屉不清楚,现在要将其找到,广度优先遍历的做法是:
- 先将第一个抽屉打开,在最外层找一遍
- 将第一个抽屉中红盒子打开,在红盒子中找一遍
- 将红盒子中绿盒子打开,在绿盒子中找一遍
- 递归查找剩余的两个盒子
深度优先遍历:将一个抽屉一次性遍历完(包括该抽屉中包含的小盒子),再去递归遍历其他盒子
具体到一个图中就是这样:
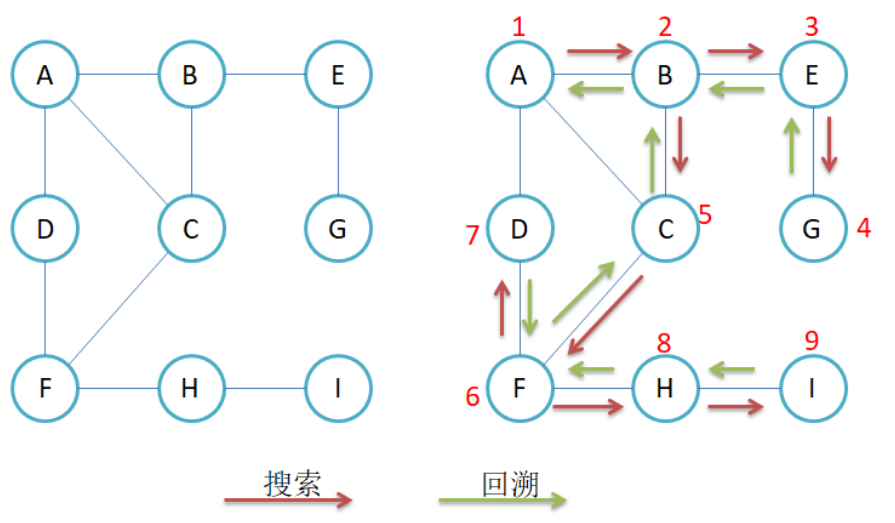
如果之前学习过递归,回溯算法的同学,相信深度优先遍历对你来说也不是什么难题, 下面就直接上手写代码了!
void DFS(const V& src)//图的深度优先遍历
{size_t srci = _index[src];vector<bool> check(_vertex.size(), false);_DFS(srci, check);
}
void _DFS(size_t srci, vector<bool>& check)
{cout << srci << ": " << _vertex[srci] << endl;check[srci] = true;for (int i = 0; i < _vertex.size(); i++)//遍历与此点相邻的所有点if (_edge[srci][i] != MAX_W && check[i] == false)_DFS(_vertex[i], check);
}
5. 图的最小生成树
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条:
- 只能使用图中的边来构造最小生成树
- 只能使用恰好n-1条边来连接图中的n个顶点
- 选用的n-1条边不能构成回路
最小生成树其实就是子图是最简单的连通图, n-1条边刚好可以连接n个顶点

每一个图的最小生成树是不唯一的. 一般通过Kruskal算法和prim算法来构造最小生成树
6. Kruskal算法讲解
首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL},其中每个顶点自成一个连通分量,其次不断从E中取出权值最小的一条边(若有多条任取其一),若该边的两个顶点来自不同的连通分量,则将此边加入到G中。如此重复,直到所有顶点在同一个连通分量上为止。
核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树
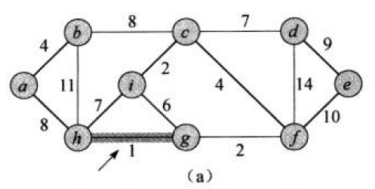
克鲁斯卡尔算法的核心就是每次都找最小的权值边, 只要这次选的边没有构成环, 就接着往下走. 比如此图中先选1,再选2,再选2,再选4,依次向后选. 可是问题是, 我怎么知道我选出来的边是否成环了. 这里就需要使用到之前的数据结构: 并查集. 即如果一条边关联的两个点在同一集合, 那么他们就成环了, 反之则不成环. 还有一点, 怎样知道图中哪条边的权值最小? 这里可以使用优先级队列
代码案例:
typedef Graph<V, W, MAX_W, Direction> Self;
struct EDGE //仿函数用于优先级队列
{int _srci;int _desti;W _w;EDGE(int srci, int desti, W w) :_srci(srci), _desti(desti), _w(w){}bool operator>(const EDGE& e) const{return _w > e._w;}
};
W Kruskal(Self& mintree)克鲁斯卡尔算法,返回权重总和
{int n = _vertex.size();mintree._vertex = _vertex;//最开始传入的最小生成树是没有初始化的,没有点和边的关系,若直接使用add会报错mintree._edge.resize(n);mintree._index = _index;for (int i = 0; i < n; i++)mintree._edge[i].resize(n, MAX_W);priority_queue<EDGE, vector<EDGE>, greater<EDGE>> minqueue;//利用优先级队列来存储边的权重大小for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)if (i < j && _edge[i][j] != MAX_W)//i<j,只用走一半,不然如果是有向图,可能会重复插入边minqueue.push(EDGE(i, j, _edge[i][j]));//将所有的边都插入优先级队列int minsize = 0;//选出n-1条边UnionFindSet ufs(n);//利用并查集来判断生成树中是否有环W totalvalue = W();//最后的返回结果while (!minqueue.empty()){EDGE min = minqueue.top();minqueue.pop();if (!ufs.SameSet(min._srci, min._desti))//如果这条边关联的两个点不在一个集合,再继续下面的操作{cout << _vertex[min._srci] << "->" << _vertex[min._desti] << ":" << min._w << endl;mintree._AddEdge(min._srci, min._desti, min._w);//增加一条边ufs.Union(min._srci, min._desti);//将这条边的两个顶点加入同一集合minsize++;//边数一直要到n-1totalvalue += min._w;//最后的结果也需要更新}}if (minsize == n - 1) return totalvalue;else return W();
}
可能大家是第一次见这样写函数, 传入一个空的图, 由于图论的复杂性和算法的特别,所以使用这种方式已经是很优解了,关于代码的解释都在注释中,若还有不懂,欢迎私信
7. prim算法讲解
prim算法的思想是,既然最小生成树包含所有的顶点. 所以我可以从任意顶点开始, 一直沿着此点向外做拓展,直到覆盖了图中所有的顶点. 算法每一步在连接集合A和A之外的结点的边中, 选择一条权值最小的加入A集合, 下图是步骤图,可以参考一下:
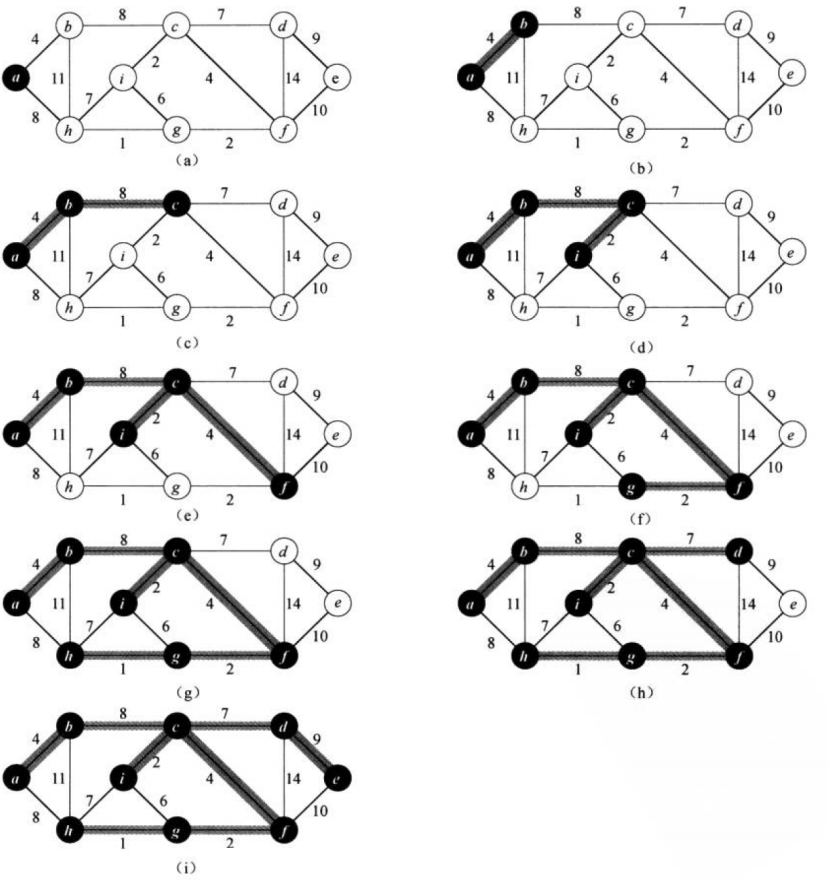
可以看见算法的每一步都在选择,当前集合A中的边的最小值,并且不会走让图成环的路径. 这个算法的实现呢,首先我们需要两个集合, A:已被选择过的点. B: 未被选择过的点. 要做的就是在已被选择的点中找权值最小,且还没选择过的点的边. 这里需要利用优先级队列,将与A集合中顶点相连的边都加入优先级队列中. 在添加边关系前,只需要判断这条边的两个顶点是否都在A集合, 如果都在,相连后就会成环. 需要pop掉这条边
直接上代码:
W Prim(Self& mintree,const V& src)//普里姆算法,返回权重总和
{size_t srci = GetIndex(src);//找到最初点的下标int n = _vertex.size();mintree._vertex = _vertex;//最开始传入的最小生成树是没有初始化的,没有点和边的关系,若直接使用add会报错mintree._edge.resize(n);mintree._index = _index;for (int i = 0; i < n; i++)mintree._edge[i].resize(n, MAX_W);unordered_set<int> x;//已被选过的顶点集合unordered_set<int> y;//未被选过的顶点集合x.insert(srci);for (int i = 0; i < n; i++)if (i != srci)y.insert(i);//从X集合中找到权值最小,并且在Y集合中的边priority_queue<EDGE, vector<EDGE>, greater<EDGE>> minqueue;//利用优先级队列,将与X集合中相关联的边都放入优先级队列,在添加边时只需要判断这条边的两个顶点是否都在X集合,若都在X集合,添加后会形成环,不可取for (size_t i = 0; i < n; i++)if (_edge[srci][i] != MAX_W)minqueue.push(EDGE(srci, i, _edge[srci][i]));//先把srci连接的边添加到队列当中W totalvalue = W();int size = 0;while (!minqueue.empty()){while (!minqueue.empty() && x.find(minqueue.top()._srci) != x.end() && x.find(minqueue.top()._desti) != x.end())//把不符合要求的边给去掉minqueue.pop();EDGE min = minqueue.top();minqueue.pop();mintree._AddEdge(min._srci, min._desti, min._w);size++;x.insert(min._desti);y.erase(min._desti);totalvalue += min._w;if (size == n - 1) break;for (int i = 0; i < n; i++)if (x.find(i) == x.end() && _edge[min._desti][i] != MAX_W)minqueue.push(EDGE(min._desti, i, _edge[min._desti][i]));//将与dest连接的所有的边都添加到优先级队列}return totalvalue;
}
若有不懂,欢迎私信
8. 总结以及拓展
关于图的最小生成树的两个算法其实都是使用的贪心策略,用局部最优找到全局最优. 但是关于这两个算法的正确性的验证这里由于篇幅有限就不多讲解了
| 脂代谢组学和蛋白质组学分析揭示多囊卵巢综合征的发病机制)
)
)

![[初学rust] 03_所有权](http://pic.xiahunao.cn/[初学rust] 03_所有权)
即将召开!)













