文章目录
- 前言
- 一、数据安全智能分类分级平台建设背景
- 二、数据安全分类分级建设思路和实践
- 1、做标签– 数据安全标签体系
- 2、打标签– 鹰眼智能打标平台 3.0
- 3、用标签– 全行统一“数据安全打标签结果”服务提供
前言
随着国家对数据安全的高度重视,以及相关法律法规的出台,数据安全领域工作得到了极大的提升。本文将分享银行运用智能化手段实现数据安全分类分级的背景、思路和方法。
一、数据安全智能分类分级平台建设背景
首先来介绍一下数据安全智能分类分级平台建设背景。
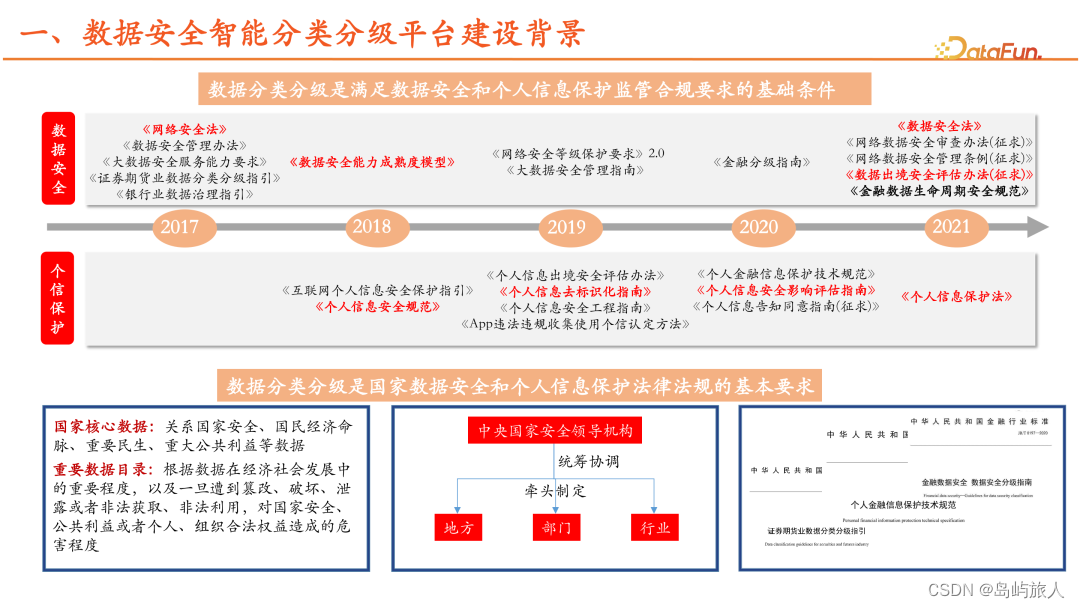
我国在 2021 年发布了《中华人民共和国数据安全法》和《中华人民共和国个人信息保护法》两大法律,将数据安全提升到了新的高度。随着监管机构发布银行保险机构的安全管理办法,以及人民银行发布《中国人民银行业务领域数据安全管理办法(征求意见稿)》,对银行业数据安全提出了非常高的要求。
在此背景下,银行注重数据分类分级&#





常用的IP修改方式(文本配置工具nmtui+配置文件+nmcli命令))








)


)

