一、说明

莫比乌斯变换在非欧几何中有及其重要的地位，而莫比乌斯变换是抽象的， 不是一眼就能识别出其特征。本篇将继续梳理它的种种特性。并给出艺术数学的文献查询地址。

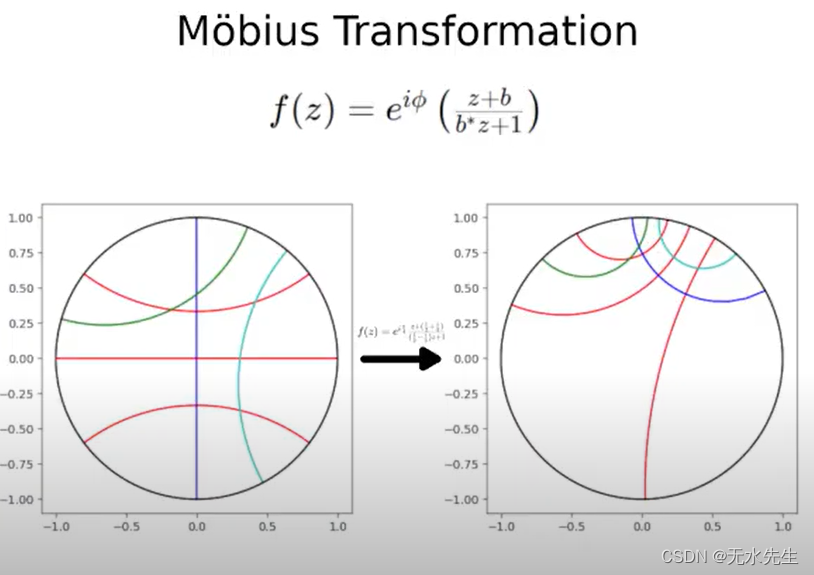
二、多视角看莫比乌斯变换

2.1 从几何角度

让我们了解一下莫比乌斯变换在不同背景下的含义。莫比乌斯变换可以从复分析和几何角度来看。在几何中，我们可以通过执行多个步骤来得到莫比乌斯变换，例如

• 从平面到单位二球体的球极投影，
• 旋转球体并将其移动到新位置，
• 空间方向，
• 从球体的新位置到平面的立体投影。
  此外，莫比乌斯变换保留角度，将每个圆映射到一条线或圆，并将每条直线映射到一条线或圆。

2.2 复分析中的莫比乌斯变换

复数函数$$w=f(z)=\frac{(az+b)}{(cz+d)};ad–bc\ne 0$$
a、b、c、d 为复数，称为莫比乌斯变换或分数线性变换。

莫比乌斯变换中的条件，即 ad – bc ≠ 0 确保以下陈述成立。

• az + b 和 cz + d 都不会相同地消失
• a 和 c 不能都等于 0，其中 f 为常数
• b 和 d 不能都等于 0，其中 f 为常数
• f(z) 的分母不能是该复数函数分子的常数倍。

2.3 莫比乌斯变换运算组合

莫比乌斯变换是四个基本映射的组合，即平移、膨胀、旋转和反转。

平移： $z\to z+z_0$使得 $z_0\in C$
膨胀：$z\to \lambda z$； $\lambda >0$ 且 $\lambda \in R$
旋转：$z\to e^{i\theta }z$； $\theta \in R$
反转：$z\to 1/z$

2.4 莫比乌斯变换的不动点

如果 $f(z_0)=z_0$，则点 $z_0\in C_{\infty }$称为复函数 $f(z)$ 的不动点。莫比乌斯变换最多可以有两个不动点，除非它是恒等映射。

如果z满足条件$f(z)=(az+b)/(cz+d)=z$，那么我们可以推导出以下方程，即$c{z}^2–(a–d)z–b=0$。

当$c=0$ 时，$z=-b/(a–d)$ 是 f 的唯一不动点，如果 $a=d$，则 $z=-b/(a–d)$ 为$\infty$。

2.5 三个点决定一个莫比乌斯变换

众所周知，莫比乌斯变换完全由其在三个不同点上的作用决定。此外，我们可以说，通过对复平面 $C_{\infty }$中 3 个不同点的作用，只有一种莫比乌斯变换是可能的。此分数线性变换组实际上是
$$\frac{a}{c}\cdot \frac{z+b{a}^{-1}}{z+d{c}^{-1}}=A\frac{z+B}{z+C}$$
因此，有三个未知数。

2.6 交叉比

假设 $z1,z2,z3,z4\in C_{\infty }$ ，使得 $z1,z2,z3,z4$的交比是由下式定义的莫比乌斯变换：

$S(z)=(z1,z2,z3,z4)=(z–z3)(z2–z4)/(z2–z3)(z–z4)$ 使得 $S(z1)=1，S(z3)=0且S(z4)=\infty$。

当 $z2=\infty$ 时，交比 $(z1,z2,z3,z4)=(z1–z3)/(z1–z4)$

当 $z3=\infty$ 时，交比 $(z1,z2,z3,z4)=(z2–z4)/(z1–z4)$

当 $z4=\infty$ 时，交比$(z1,z2,z3,z4)=(z1–z3)/(z2–z3)$

2.7 莫比乌斯变换的逆变换

考虑莫比乌斯变换 f(x) = (az + b)/(cz +d) 从复平面到复平面的可逆。然后，f(z) 的逆，即 f -1 (z) 又是莫比乌斯变换，给出如下：

$$f-1(z)=(dz–b)/(-cz+a)。$$

三 莫比乌斯变换性质证明

3.1 证明1：莫比乌斯变换将圆变成圆。

解决：

考虑一个复函数 $w=u+iv$，使得 $z=x+iy$。由此，我们可以写出以下内容：

$u=x/(x2+y2)$
$v=-y/(x2+y2)$
$x=u/(u2+v2)$
$y=-v/(u2+v2)$

我们知道，莫比乌斯变换是平移、扩张和反转的组合。而且，很容易证明平移和扩张将圆变成圆。那么，让我们验证一下圆到圆的反转。

考虑圆的一般方程：
$$A(x2+y2)+BX+Cx+D=0$$

现在，应用变换 $w=1/z$。因此，将 $x=u/(u2+v2)$ 和 $y=-v/(u2+v2)$代入给定的圆方程中。因此，
$$\begin{array}{l}A\left[{\left(\frac{u}{u^2+v^2}\right)}^2+{\left(\frac{-v}{u^2+v^2}\right)}^2\right]+B\left(\frac{u}{u^2+v^2}\right)+C\left(\frac{-v}{u^2+v^2}\right)+D=0\end{array}$$

经过简化，我们得到；
$$\begin{gathered} \Rightarrow A[1/(u2+v2)+B[u/(u2+v2)]+C[-v/(u2+v2)]+D=0 \\ \Rightarrow A[1/(u2+v2)+B[u/(u2+v2)]+C[-v/(u2+v2)]+D=0 \\ \Rightarrow [A+Bu+-Cv+D(u2+v2)]/(u2+v2)=0 \\ \Rightarrow D(u2+v2)]+Bu–Cv+A=0 \end{gathered}$$

这又是一个圆方程。这意味着反转保留了圆圈。
由此证明。

3.2 证明2：寻找莫比乌斯变换不动点

找到 f(z) = (3z – 1)/(z + 5) 的不动点。
解决：
鉴于，$f(z)=(3z–1)/(z+5)$
令 $f(z)=z$

这意味着 $(3z–1)/(z+5)=z$
$3z–1=z(z+5)$
$3z–1=z^2+5z$
$\Rightarrow z^2+5z–3z+1=0$
$\Rightarrow z^2+2z+1=0$
$\Rightarrow (z+1{)}^2=0$
$\Rightarrow z=-1$

3.3 证明3：寻找一个莫比乌斯变换拥有两个不动点

给定两个点，找到拥有这两个不动点的莫比乌斯变换。如：找到具有两个不动点（即 3i 和 1 + i）的莫比乌斯变换。

解决：

假设$3i$ 和 $1+i$ 是莫比乌斯变换的两个不动点。
设 α 和 β 为两个不动点。
这意味着 $\alpha =3i$ 且 $\beta =1+i$。
众所周知，$cz2–(a–d)z–b=0$
这可以写成 $cz2–(a–d)z–b=(z–\alpha )(z–\beta )$

由此，我们可以写出以下内容：

$c=1$
$a–d=\alpha +\beta =3i+1+i=1+4i$
$b=-\alpha \beta =-(3i)(1+i)=-(3i+3i2)=3-3i$
令 k 为除 α 或 β 之外的任何常数。
那么具有给定不动点的一组可能的解是：

$a=k$ 且 $d=k-\alpha -\beta$

我们知道，

$$f(z)=(az+b)/(cz+d)$$

现在，通过替换上述值，我们得到；

$$f(z)=(kz–\alpha \beta )/(z+k–\alpha –\beta )$$

让我们假设$k=1$。

因此，$f(z)=(z+3–3i)/(z+1–1–4i)$，最后：

$$f(z)=(z+3–3i)/(z–4i)$$

四、艺术的莫比乌斯变换

应该指出的是，$S^n$ 的共形变换群的非紧性是一个不平凡的现象，它与每个人的几何直觉相矛盾。完全不清楚为什么存在 $S^n$的单一共形变换，这不是刚性旋转。类似地，没有配备数学机器的普通眼睛无法看到 R^n 的任何非平凡的保角变换（正如我们所知，它将圆形球体映射到圆形球体），其中“平凡”指的是相似变换。

即使是具有几何思维的艺术家、对称图案的设计师，也无法克服人类想象力的这一限制。如果我们看看世界各地几个世纪以来设计的数量惊人的装饰品，我们会看到各种平移和旋转对称，但从未看到共形对称。然而，近年来，共角对称在埃舍尔的许多美丽的画作中得到了体现。然而，这些想法是由一位数学家考克塞特( Coxeter) 传达给艺术家的。
参考：(G. d’Ambra and M. Gromov, Lectures on transformation groups: Geometry and Dynamics, in: Surveys in Differential Geometry, 1, 1991.)