数据结构复习指导之串的模式匹配

文章目录

串的模式匹配

考纲内容

复习提示

1.简单的模式匹配算法

知识回顾

2.串的模式匹配算法——KMP算法

2.1字符串的前缀、后缀和部分匹配值

2.2KMP算法的原理是什么

3.KMP算法的进一步优化

串的模式匹配

考纲内容

字符串模式匹配

复习提示

本章是统考大纲第6章内容,采纳读者建议单独作为一章,大纲只要求掌握字符串模式匹配，重点掌握 KMP 匹配算法的原理及 next数组的推理过程，手工求 next 数组可以先计算出部分匹配值表然后变形，或根据公式来求解。了解nextval数组的求解方法。

1.简单的模式匹配算法

子串的定位操作通常称为串的模式匹配，它求的是子串(常称模式串)在主串中的位置。这里采用定长顺序存储结构，给出一种不依赖于其他串操作的暴力匹配算法。

int Index(sString S,sString T){int i=1,j=1;while(i<=S.length && j<=T.length){if(S.ch[i]==T.ch[j]){++i; ++j;            //继续比较后继字符
}       else{i=i-j+2; j=1;        //指针后退重新开始匹配
}
}if(j>T.length) return i-T.length;else return 0;
}

在上述算法中，分别用计数指针 i 和 j 指示主串S和模式串T中当前正待比较的字符位置。

算法思想为:从主串S的第一个字符起，与模式串T的第一个字符比较，若相等，则继续逐个比较后续字符;否则从主串的下一个字符起，重新和模式串的字符比较;以此类推，直至模式串T中的每个字符依次和主串S中的一个连续的字符序列相等，则称匹配成功，函数值为与模式串T中第一个字符相等的字符在主串S中的序号，否则称匹配不成功，函数值为零。图 4.2展示了模式串 T='abcac'和主串S的匹配过程，每次匹配失败后，都把模式串T后移一位。

简单模式匹配算法的最坏时间复杂度为 O(nm)，其中n和m分别为主串和模式串的长度。

例如，当模式串为'0000001'而主串为'0000000000000000000000000000000000000000 000001'时，由于模式串中的前6个字符均为"0'，主串中的前 45 个字符均为'0'，每趟匹配都是比较到模式串中的最后一个字符时才发现不等，指针i需要回溯 39 次，总比较次数为 40x7=280 次。

知识回顾

2.串的模式匹配算法——KMP算法

根据图 4.2 的匹配过程，在第三趟匹配中，i=7、j=5 的字符比较，结果不等，于是又从 i=4、j=1 重新开始比较。然而，仔细观察会发现，i=4和 j=1，i=5 和j=1及 i=6和 j=1 这三次比较都是不必进行的。从第三趟部分匹配的结果可知，主串的第4个、第5个和第6个字符是'b'、'c'和'a'(即模式串的第2 个、第3个和第4个字符)，因为模式串的第1个字符是'a'，所以无须再和这三个字符进行比较,而只需将模式串向右滑动三个字符的位置,继续进行 i=7、j=2 时的比较即可。

在暴力匹配中，每趟匹配失败都是模式串后移一位再从头开始比较。而某趟已匹配相等的字符序列是模式串的某个前缀，这种频繁的重复比较相当于模式串不断地进行自我比较，这就是其低效率的根源。因此，可以从分析模式串本身的结构着手，若已匹配相等的前缀序列中有某个后缀正好是模式串的前缀，则可将模式串向后滑动到与这些相等字符对齐的位置，主串 i 指针无须回溯，并从该位置开始继续比较。而模式串向后滑动位数的计算仅与模式串本身的结构有关，而与主串无关(这里理解起来比较困难，没关系，带着这个问题继续往后看)。

2.1字符串的前缀、后缀和部分匹配值

要了解子串的结构，首先要弄清楚几个概念:前缀、后缀和部分匹配值。

前缀指除最后一个字符以外，字符串的所有头部子串；

后缀指除第一个字符外，字符串的所有尾部子串；

部分匹配值则为字符串的前缀和后缀的最长相等前后缀长度。下面以'ababa'为例进行说明:

'a'的前缀和后缀都为空集，最长相等前后缀长度为0。
'ab'的前缀为{a}，后缀为{b}，{a}n{b}=Ø，最长相等前后缀长度为 0。
'aba'的前缀为{a,ab}，后缀为{a,ba}，{a,ab}n{a,ba}={a}，最长相等前后缀长度为 1。
'abab'的前缀{a,ab,aba}n后缀{b,ab,bab}={ab}，最长相等前后缀长度为 2.
'ababa'的前缀{a,ab,aba,abab}∩后缀{a,ba,aba,baba}={a,aba}，公共元素有两个，最长相等前后缀长度为3。

因此，字符串'ababa'的部分匹配值为 00123.

这个部分匹配值有什么作用呢?
回到最初的问题，主串为 ababcabcacbab，子串为abcac。
利用上述方法容易写出子串'abcac'的部分匹配值为 00010，将部分匹配值写成数组形式，就得到了部分匹配值(Partial Match，PM)的表。

下面用 PM 表来进行字符串匹配：

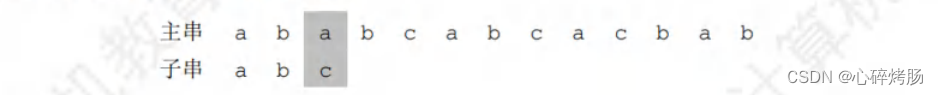
第一趟匹配过程:
发现 c与a不匹配，前面的2个字符'ab'是匹配的，查表可知，最后一个匹配字符b对应的部分匹配值为0，因此按照下面的公式算出子串需要向后移动的位数:
移动位数=已匹配的字符数-对应的部分匹配值
因为2-0=2，所以将子串向后移动2位，如下进行第二趟匹配:

第二趟匹配过程:
发现 c与b不匹配，前面4个字符'abca'是匹配的，最后一个匹配字符a对应的部分匹配值为1，4-1=3，将子串向后移动3位，如下进行第三趟匹配:

第三趟匹配过程:
子串全部比较完成，匹配成功。整个匹配过程中，主串始终没有回退，所以KMP算法可以在 O(n+m)的时间数量级上完成串的模式匹配操作，大大提高了匹配效率。

某趟发生失配时，若对应的部分匹配值为 0，则表示已匹配相等序列中没有相等的前后缀，此时移动的位数最大，直接将子串首字符后移到主串当前位置进行下一趟比较:若已匹配相等序列中存在最大相等前后缀(可理解为首尾重合)，则将子串向右滑动到和该相等前后缀对齐(这部分字符下一趟显然不需要比较)，然后从主串当前位置进行下一趟比较。

2.2KMP算法的原理是什么

我们刚刚学会了怎样计算字符串的部分匹配值、怎样利用子串的部分匹配值快速地进行字符串匹配操作，但公式“移动位数=已匹配的字符数-对应的部分匹配值”的意义是什么呢?

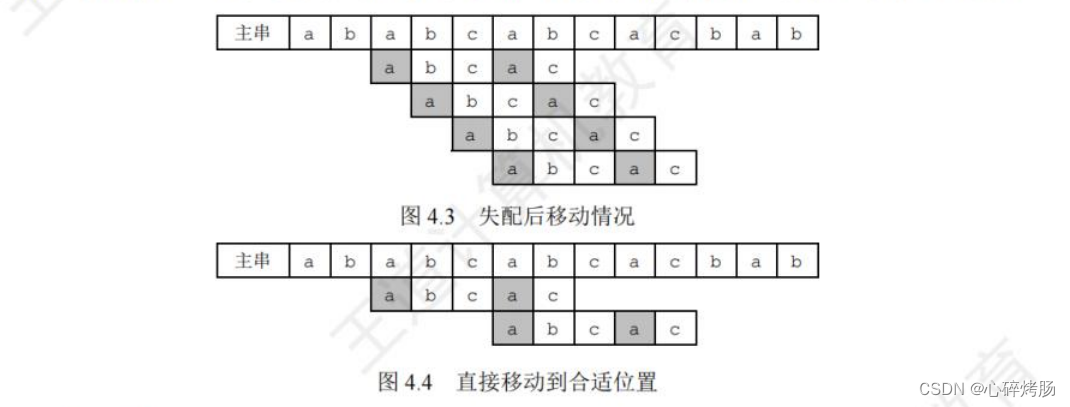
如图4.3所示，当c与b不匹配时，已匹配'abca'的前缀a和后缀a为最长公共元素。已知前缀a与 b、c均不同，与后缀a相同，因此无须比较，直接将子串移动“已匹配的字符数-对应的部分匹配值”，用子串前缀后面的元素与主串匹配失败的元素开始比较即可，如图 4.4所示。

对算法的改进方法:
已知：右移位数=已匹配的字符数-对应的部分匹配值。
写成：Move=(j-1)-PM[j-1]。
使用部分匹配值时，每当匹配失败，就去找它前一个元素的部分匹配值，这样使用起来有些不方便，所以将 PM 表右移一位，这样哪个元素匹配失败，直接看它自己的部分匹配值即可。

将上例中字符串'abcac'的PM 表右移一位，就得到了next 数组:

我们注意到:
1) 第一个元素右移以后空缺的用-1来填充，因为若是第一个元素匹配失败，则需要将子串向右移动一位，而不需要计算子串移动的位数。
2) 最后一个元素在右移的过程中溢出，因为原来的子串中，最后一个元素的部分匹配值是其下一个元素使用的，但显然已没有下一个元素，所以可以舍去。

这样，上式就改写为
Move=(j-1)-next[j]
相当于将子串的比较指针 j 回退到
j=j-Move=j-((j-1)-next[j])=next[j]+1
有时为了使公式更加简洁、计算简单，将next 数组整体+1。
因此，上述子串的 next 数组也可以写成：

[命题追踪——KMP 匹配过程中指针变化的分析]

最终得到子串指针变化公式 j=next[ j ]。在实际匹配过程中，子串在内存中是不会移动的，而是指针发生变化，画图举例只是为了让问题描述得更形象。next[ j ]的含义是:当子串的第 j 个字符与主串发生失配时，跳到子串的 next[ j ]位置重新与主串当前位置进行比较。

如何推理 next 数组的一般公式?设主串为' $s_{1}s_{2}...s_{n}$ '，模式串为 $'p_{1}p_{2}...p_{m}'$ ，当主串中第 i 个字符与模式串中第 j 个字符失配时,子串应向右滑动多远,然后与模式中的哪个字符比较?

假设此时应与模式串的第k(k<j)个字符继续比较，则模式串中前 k-1 个字符的子串必须满足下列条件，且不可能存在 k'>k 满足下列条件:
$p_{1}p_{2}...p_{k-1}=p_{j-k+1}p_{j-k+2}...p_{j-1}$

若存在满足如上条件的子串，则发生失配时，仅需将模式串向右滑动至模式串的第k个字符和主串的第i个字符对齐，此时模式串中的前k-1 个字符的子串必定与主串中第i个字符之前长度为 k-1 的子串相等，由此，只需从模式串的第k个字符与主串的第i个字符继续比较即可,如图 4.5 所示。

当模式串已匹配相等序列中不存在满足上述条件的子串时(可视为 k=1)，显然应该将模式串右移 j-1 位，让主串的第 i 个字符和模式串的第1个字符进行比较，此时右移位数最大。

当模式串的第1个字符(j=1)与主串的第i个字符发生失配时，规定 next[1]=0（可理解为将主串的第i个字符和模式串的第1个字符的前面空位置对齐，即模式串右移一位。）将模式串右移一位，从主串的下一个位置(i+1)和模式串的第1个字符继续比较。

通过上述分析可以得出 next 函数的公式:

上述公式不难理解，实际做题求 next 值时，用之前的方法也很好求，但要想用代码来实现，貌似难度还真不小，我们来尝试推理求解的科学步骤。
首先由公式可知

next[1]=0

设 next[j]=k，此时k应满足的条件在上文中已描述。
此时 next[ j+1 ]=?可能有两种情况:
(1)若 $p_{k}=p_{j}$ ，则表明在模式串中

$p_{1}...p_{k-1}p_{k}=p_{j-k+1}...p_{j-1}p_{j}$

并且不可能存在 k'>k 满足上述条件，此时 next[ j+1 ]=k+1，即 next[ j+1 ] = next[ j ]+1

(2)若 $p_{k}\neq p_{j}$ ，则表明在模式串中

$p_{1}...p_{k-1}p_{k}\neq p_{j-k+1}...p_{j-1}p_{j}$

此时可将求 next 函数值的问题视为一个模式匹配的问题。用前缀 $p_{1}...p_{k}$ 去与后缀 $p_{j-k+1}...p_{j}$ 匹配，当 $p_{k}\neq p_{j}$ 时，应将 $p_{1}...p_{k}$ 向右滑动至以第 next [k]个字符与 $p_{j}$ 比较，若 $p_{next[k]}$ 与 $p_{j}$ 仍不匹配,则需要寻找长度更短的相等前后缀,下一步继续用 $p_{next[next[k]]}$ 与 $p_{j}$ 比较,以此类推,直到找到某个更小的 k'=next[next… [k]](1<k'<k<j)，满足条件

$p_{1}...p_{k}=p_{j-k'+1}...p_{j}$

则 next [ j+1 ]=k'+1

也可能不存在任何 k'满足上述条件,即不存在长度更短的相等前缀后缀,令 next[ j+1 ]=1

理解起来有一点费劲?下面举一个简单的例子。

图 4.6的模式串中已求得6个字符的next值,现求 next [7],因为next[ 6 ]=3,又 $p_{6}\neq p_{3}$ 则需比较 $p_{6}$ 和 $p_{1 }$ (因next[ 3 ]=1),由于 $p_{6}\neq p_{1}$ ,,而next[1]=0,因此

next [7]=1；求next [8]，因 $p_{7}=p_{1}$ ,则next [8]=next [7]+1=2;求next [9]，因 $p_{8}=p_{2}$ ,则 next [9]=3。

通过上述分析写出求 next 值的程序如下:

void get_next(SString T,int next[]){int i=1，j=0;next[1]=0;while(i<T.length){if(j==0||T.ch[i]==T.ch[j]){++i; ++j;next[i]=j;    //若pi=pj，则 next[j+1]=next[j]+1}elsej=next[j];    //否则令j=next[j]，循环继续}
}

计算机执行起来效率很高，但对于我们手工计算来说会很难。因此，当我们需要手工计算时还是用最初的方法。

与 next 数组的求解相比,KMP 的匹配算法相对要简单很多，它在形式上与简单的模式匹配算法很相似。不同之处仅在于当匹配过程产生失配时，指针i不变，指针 j退回到 next[j]的位置并重新进行比较，并且当指针j为0时，指针i和j同时加 1。即若主串的第i个位置和模式串的第1个字符不等，则应从主串的第 i+1个位置开始匹配。具体代码如下:

int Index_KMP(SString S,SString T,int next[]){int i=1，j=1;while(i<=S.length && j<=T.length){if(j==0||S.ch[i]==T.ch[j]){++i; ++j;         //继续比较后继字符}elsej=next[j];        //模式串向右移动}if(j>T.length)return i-T.length;    //匹配成功elsereturn 0;
}

[命题追踪——KMP 匹配过程中比较次数的分析]

尽管普通模式匹配的时间复杂度是 O(mn)，KMP 算法的时间复杂度是 O(m+n)，但在一般情况下，普通模式匹配的实际执行时间近似为 0(m+n)，因此至今仍被采用。KMP 算法仅在主串与子串有很多“部分匹配”时才显得比普通算法快得多，其主要优点是主串不回溯。

3.KMP算法的进一步优化

前面定义的 next 数组在某些情况下尚有缺陷，还可以进一步优化。如图 4.7 所示，模式串' aaaab '在和主串' aaabaaaab '进行匹配时:

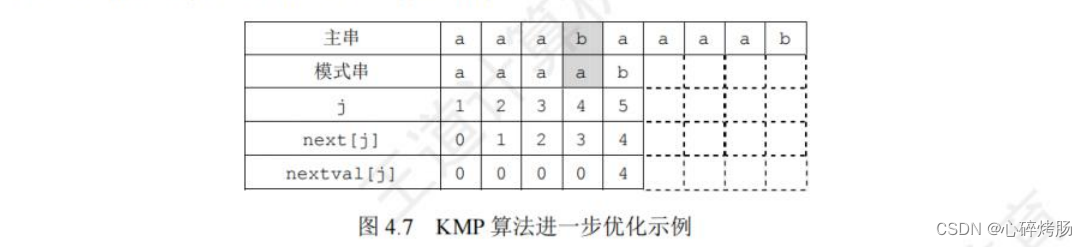
（s1，p1等数字均为脚标）

当 i=4、j=4 时，s4跟p4(b≠a)失配，若用之前的 next 数组，则还需要进行 s4与p3、s4与p2、s4与p1这3次比较。事实上，因为 $p_{next[4]=3}=p_{4}=a$

$p_{next[3]=2}=p_{3}=a$ 、 $p_{next[2]=1}=p_{2}=a$ ，显然后面3次用一个和p4相同的字符跟s4比较毫无意义，必然失配。那么问题出在哪里呢?

问题在于不应该出现 $p_{j}=p_{next[j]}$ 。理由是:当 $p_{j}\neq s_{j}$ 时，下次匹配必然是 $p_{next[j]}$ 跟 $s_{j}$ 比较,若 $p_{j}=p_{next[j]}$ ,则相当于拿一个和 $p_{j}$ 相等的字符跟 $s_{j}$ 比较，这必然导致继续失配，这样的比较毫无意义。若出现 $p_{j}=p_{next[j]}$ 则如何处理呢?

若出现 $p_{j}=p_{next[j]}$ ，则需要再次递归，将next [j] 修正为next [next [j] ]，直至两者不相等为止，更新后的数组命名为 nextval。计算 next 数组修正值的算法如下，此时匹配算法不变。

void get_nextval(SString T,int nextval[]){int i=1，j=0;nextval[1]=0;while(i<T.length){if(j==0||T.ch[i]==T.ch[j]){++i; ++j;if(T.ch[i]!=T.ch[j])  nextval[i]=j;else nextval[i]=nextval[j];}elsej=nextval[j];}
}

KMP 算法对于初学者来说可能不太容易理解，读者可以尝试多读几遍本章的内容，并参考一些其他教材的相关内容来巩固这个知识点。