【强训笔记】day4

NO.1
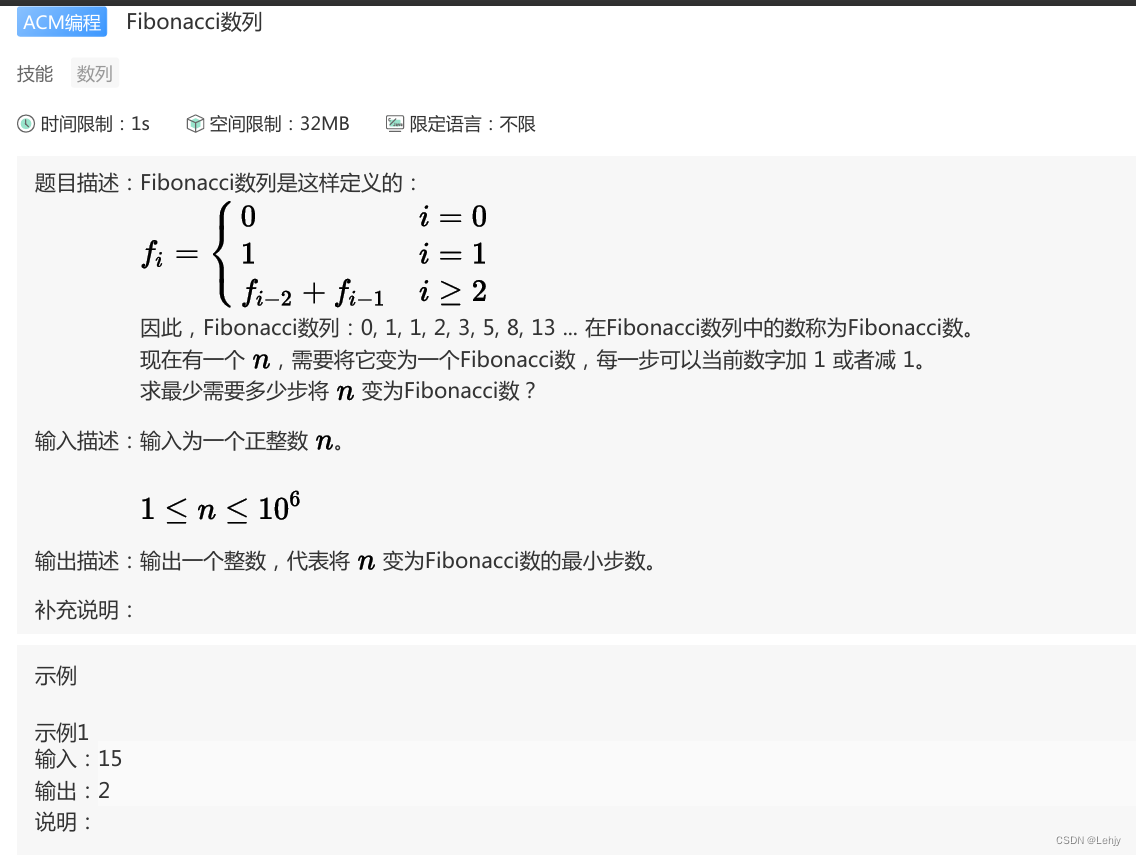
在这里插入图片描述
思路：利用滚动数组，迭代一个Fibonacci数列，给出三个值进行循环迭代，当n<c时，说明n在b和c之间，这里只需要返回c-n和n-b的最小值就可以了。
代码实现：

#include<iostream>using namespace std;int main()
{int n;cin >> n;int a = 0, b = 1, c = 1;while (n > c){a = b;b = c;c = a + b;}cout << min(c - n, n - b) << endl;return 0;
}

NO.2
在这里插入图片描述
代码实现：

class Solution
{int m, n;bool vis[101][101] = { 0 };int dx[4] = { 0, 0, 1, -1 };int dy[4] = { 1, -1, 0, 0 };
public:bool exist(vector<string>& board, string word){m = board.size(), n = board[0].size();for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (board[i][j] == word[0]){if (dfs(board, i, j, word, 0)) return true;}}}return false;}bool dfs(vector<string>& board, int i, int j, string& word, int pos){if (pos == word.size() - 1){return true;}vis[i][j] = true;for (int k = 0; k < 4; k++){int a = i + dx[k], b = j + dy[k];if (a >= 0 && a < m && b >= 0 && b < n && !vis[a][b] && board[a][b]== word[pos + 1]){if (dfs(board, a, b, word, pos + 1)) return true;}}vis[i][j] = false;return false;}
};

NO.3
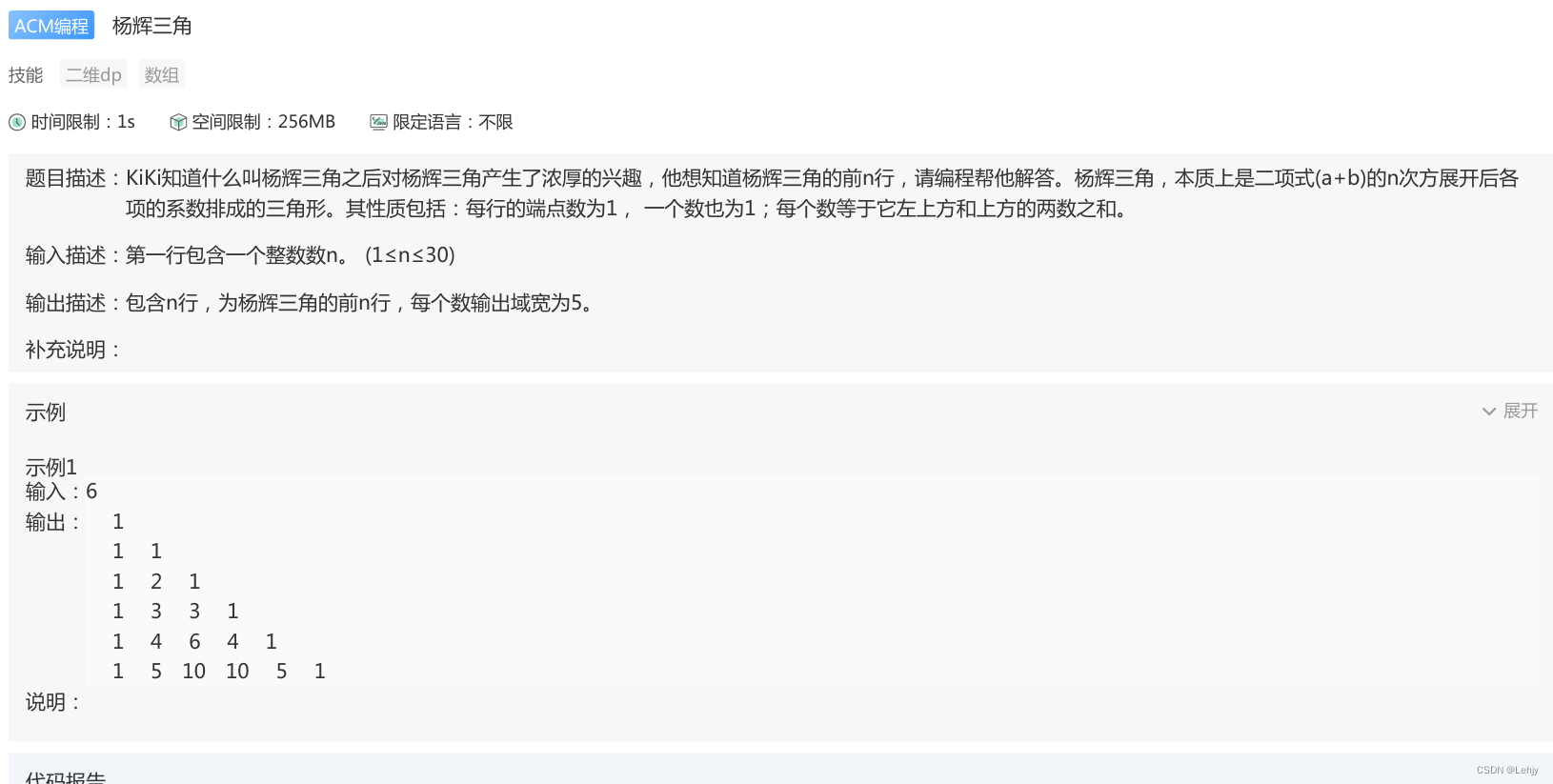
在这里插入图片描述
思路：dp线性数组，dp[1][1]=1,在根据状态方程dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1]进行求解。

#include<iostream>using namespace std;
int dp[31][31];
int n;
int main()
{cin >> n;dp[1][1] = 1;for (int i = 2; i < n; i++){for (int j = 1; j <= i; j++){dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];}}for (int i = 1; i < n; i++){for (int j = 1; j <= i; j++){printf("%5d", dp[i][j]);}printf("\n");}return 0;
}