文章目录
- 电机控制专题(一)——最大转矩电流比MTPA控制
- 前言
- 理论推导
- 仿真验证
- 轻载1N·m
- 重载30N·m
- 总结
电机控制专题(一)——最大转矩电流比MTPA控制
前言
MTPA全称为Max Torque Per Ampere,从字面意思就可以知道MTPA算法的目的是一个寻优最值问题,可以从以下两个角度理解。
- 在同一电磁转矩需求下,如何利用最小幅值的定子电流来产生;
- 在同一额定电流情况下,如何合理利用定子电流产生最大的电磁转矩。
本文先从理论推导开始,再到仿真验证MTPA算法,总结MTPA的相关知识。
纯小白,如有不当,轻喷,还请指出。
理论推导
记转矩角(电流矢量与d轴夹角)为 γ \gamma γ,则dq轴电流可以表示如下:
i d = I s c o s γ i_d=I_s cos\gamma id=Iscosγ (1)
i q = I s s i n γ i_q=I_s sin\gamma iq=Issinγ (2)
其中 I s I_s Is为定子电流幅值。
dq轴下PMSM的转矩方程为:
T e = 3 2 p n i q ψ + ( L d − L q ) i d i q T_e = \frac{3}{2}p_ni_q\psi+(L_d-L_q)i_di_q Te=23pniqψ+(Ld−Lq)idiq(3)
其中 p n p_n pn为极对数, ψ \psi ψ为永磁体磁链, L d , L q L_d,L_q Ld,Lq为分别为dq轴的电感。式(4)右边的第一项成为永磁转矩,第二项称为磁阻转矩。
将式(1)(2)代入式(3)并化简可得
T e = 3 2 p n I s ψ s i n γ + 3 4 p n I s 2 ( L d − L q ) s i n 2 γ T_e=\frac{3}{2}p_nI_s\psi sin\gamma + \frac{3}{4}p_nI_s^2(L_d-L_q)sin2\gamma Te=23pnIsψsinγ+43pnIs2(Ld−Lq)sin2γ (4)
MTPA可以从两个角度理解
- 最小的电流产生同等大的电磁转矩
- 同等大小的定子电流产生最大的电磁转矩
因此从第二个角度理解MTPA,就变成了求(4)式的在 I s I_s Is恒定,以转矩角 γ \gamma γ为变量的极值问题。
对(4)式求偏导并另其等于0,化简可得:
∂ T e ∂ γ = 2 I s ( L d − L q ) c o s 2 γ + ψ c o s γ − I s ( L d − L q ) = 0 \frac{\partial T_e}{\partial \gamma}=2I_s(L_d-L_q)cos^2\gamma +\psi cos\gamma -I_s(L_d-L_q)=0 ∂γ∂Te=2Is(Ld−Lq)cos2γ+ψcosγ−Is(Ld−Lq)=0 (5)
(5)式是一个一元二次方程,利用求根公式可解得
c o s γ 1 = − ψ + ψ 2 + 8 I s 2 ( L d − L q ) 4 I s ( L d − L q ) , c o s γ 2 = − ψ − ψ 2 + 8 I s 2 ( L d − L q ) 4 I s ( L d − L q ) cos \gamma_1 = \frac{-\psi + \sqrt{\psi^2+8I_s^2(L_d-L_q)}}{4I_s(L_d-L_q)} ,cos \gamma_2 = \frac{-\psi -\sqrt{\psi^2+8I_s^2(L_d-L_q)}}{4I_s(L_d-L_q)} cosγ1=4Is(Ld−Lq)−ψ+ψ2+8Is2(Ld−Lq),cosγ2=4Is(Ld−Lq)−ψ−ψ2+8Is2(Ld−Lq) (6)
求解得到的两个转矩角究竟哪一个是我们想要的呢?
容易注意到 ψ < ψ 2 + 8 I s 2 ( L d − L q ) 2 \psi < \sqrt{\psi^2+8I_s^2(L_d-L_q)^2} ψ<ψ2+8Is2(Ld−Lq)2,且绝大多数的IPMSM的d轴电感小于q轴电感。因此 c o s γ 1 < 0 , c o s γ 2 > 0 cos\gamma_1<0,cos\gamma_2>0 cosγ1<0,cosγ2>0。
MTPA就是要利用电机的凸极效应,合理分配定子电流一部分作为 i d i_d id,另一部分作为 i q i_q iq, i d i_d id可以用于产生磁阻转矩(电磁转矩式3等式右边的第二项)。因此d轴电流只能是负的。
那么由式(1)可知 c o s γ < 0 cos \gamma<0 cosγ<0。
因此真正能实现MTPA的转矩角为
γ = a r c c o s ( − ψ + ψ 2 + 8 I s 2 ( L d − L q ) 4 I s ( L d − L q ) ) \gamma =arccos( \frac{-\psi +\sqrt{\psi^2+8I_s^2(L_d-L_q)}}{4I_s(L_d-L_q)}) γ=arccos(4Is(Ld−Lq)−ψ+ψ2+8Is2(Ld−Lq)) (7)
此时的d轴电流和q轴电流可计算得
i d = I s c o s γ = I s − ψ + ψ 2 + 8 I s 2 ( L d − L q ) 4 ( L d − L q ) i_d = I_scos\gamma =I_s \frac{-\psi +\sqrt{\psi^2+8I_s^2(L_d-L_q)}}{4(L_d-L_q)} id=Iscosγ=Is4(Ld−Lq)−ψ+ψ2+8Is2(Ld−Lq) (8)
i q = I s 2 − i d 2 i_q=\sqrt{I_s^2-i_d^2} iq=Is2−id2 (9)
值得一提的是,转速环的输出应当是转矩指令值,而转矩和电流存在一定的线性关系,因此可以直接作为电流指令值。最简单的矢量控制 i 0 ≡ 0 i_0 \equiv0 i0≡0中,转速环的输出直接作为q轴电流的指令值;而在MTPA中,转速环输出的转矩指令值,应当由整个全部的定子电流来提供,即转速环的输出为定子电流幅值指令值,而非q轴电流指令。
仿真验证
为了直观看出使用MTPA的有效性,对一台具有高凸极比IPMSM(磁阻转矩成分更大)进行仿真。
仿真参数设置如下:
L d = 3.5 m H , L q = 12 m H , ψ = 0.17 W b , U d c = 311 V L_d= 3.5mH,L_q=12mH,\psi=0.17Wb,U_{dc}=311V Ld=3.5mH,Lq=12mH,ψ=0.17Wb,Udc=311V
转速500rpm,带轻载(1Nm)和带重载(30Nm)工况下运行。0.1s之前施加 i d ≡ 0 i_d\equiv0 id≡0控制,0.1s后施加MTPA算法,总仿真时间0.2s。
轻载1N·m
dq轴电流和三相电流波形图下
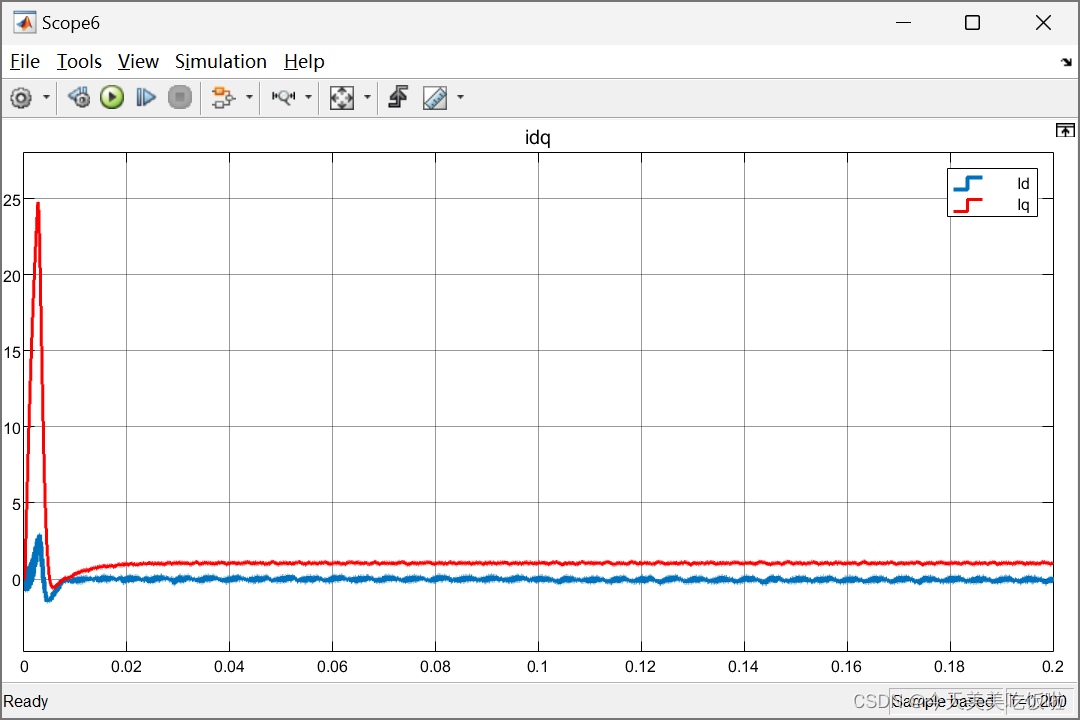
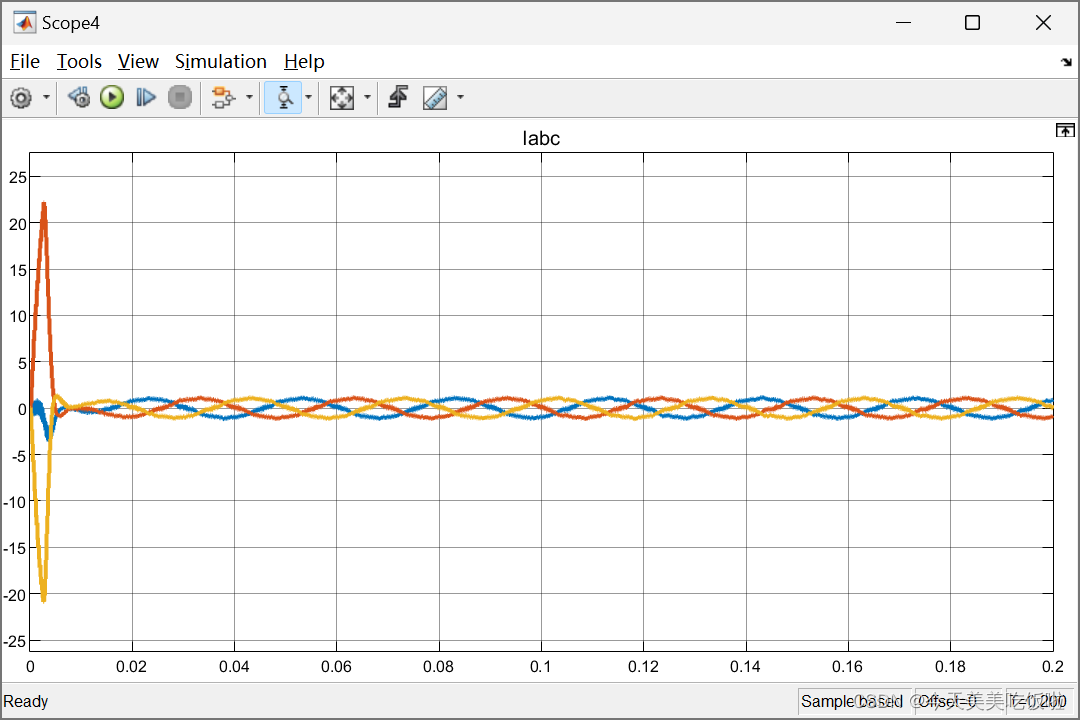
可见在施加MTPA控制之后并没有明显的效果。
原因如下:
由于所带负载较小,定子电流的幅值也小。此时的转矩角
γ = a r c c o s ( − ψ + ψ 2 + 8 I s 2 ( L d − L q ) 4 I s ( L d − L q ) ) ≈ a r c c o s ( − ψ + ψ 2 4 I s ( L d − L q ) ) = 90 ° \gamma =arccos( \frac{-\psi +\sqrt{\psi^2+8I_s^2(L_d-L_q)}}{4I_s(L_d-L_q)})\approx arccos(\frac{-\psi+\sqrt{\psi^2}}{4I_s(L_d-L_q)})=90\degree γ=arccos(4Is(Ld−Lq)−ψ+ψ2+8Is2(Ld−Lq))≈arccos(4Is(Ld−Lq)−ψ+ψ2)=90°
此时的d轴电流指令值 I d ≈ I s c o s γ = 0 I_d\approx I_scos\gamma =0 Id≈Iscosγ=0。
所以施加MTPA之后,并没有客观的负的d轴电流来产生磁阻转矩。
重载30N·m
dq轴电流和三相电流波形图如下
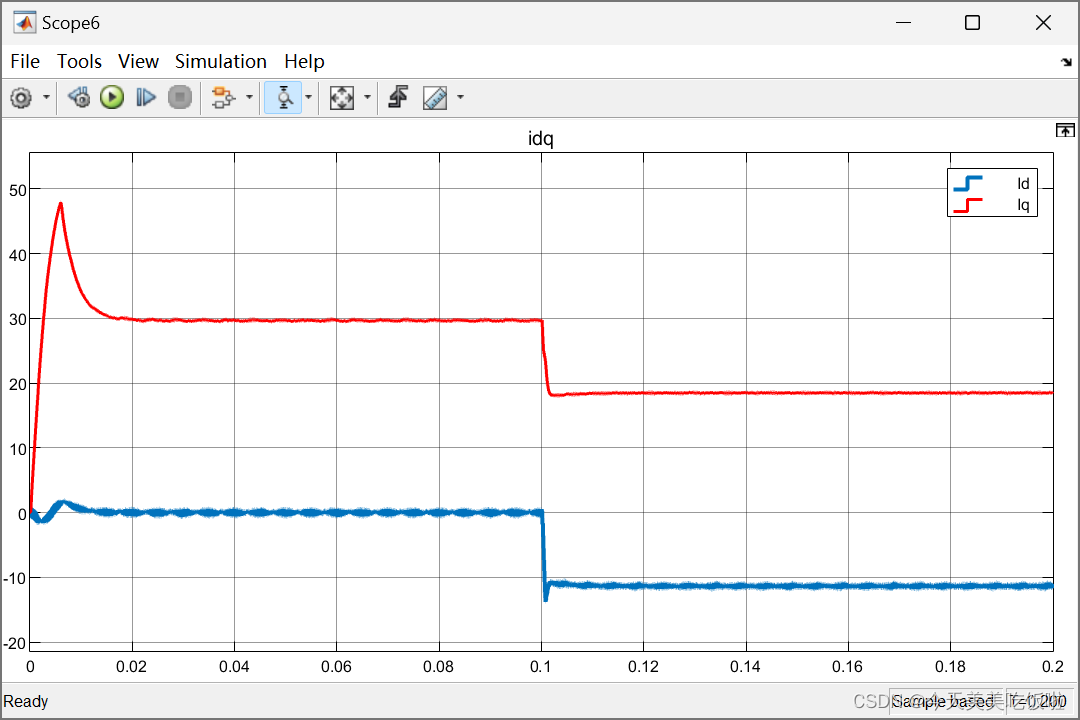
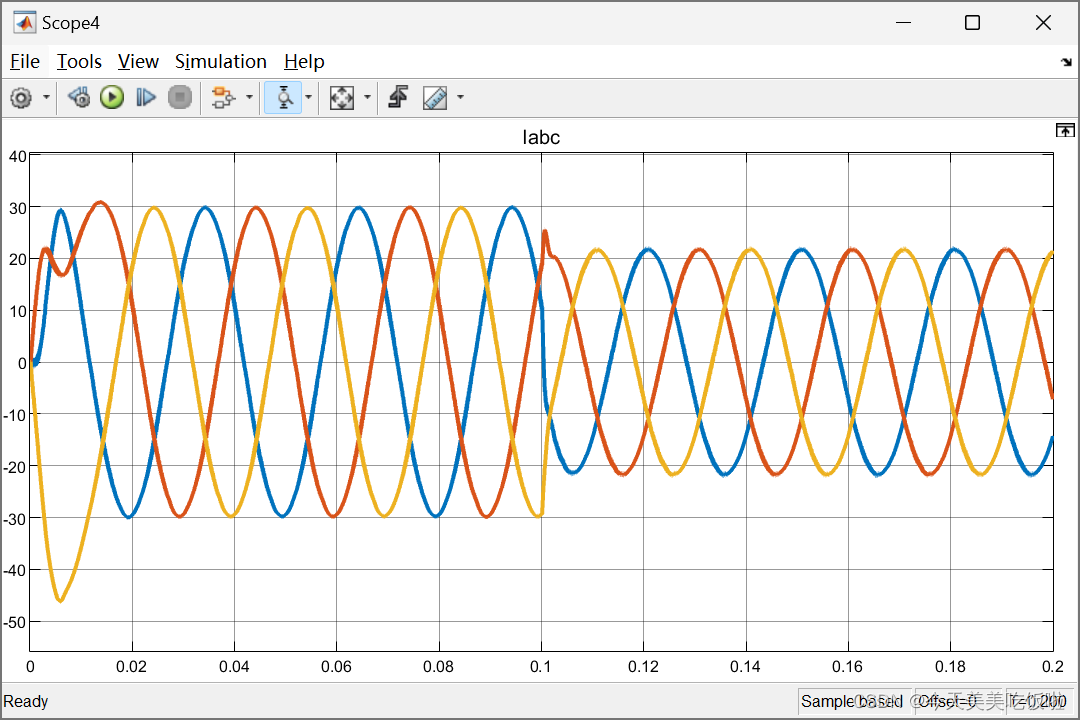
仿真结果说明,在带重载的情况下,所需的电磁转矩大,施加MTPA控制以后,d轴指令值从0变为-10A,q轴指令值从30降为18A,即利用了电机的凸极效应,合理分配了相电流以产生磁阻转矩。
从三相电流波形可以看出,施加MTPA后,定子电流幅值从30A减为20A,即使用更小的定子电流产生同等的电磁转矩,此即MTPA的目的。
总结
MTPA算法的目的在于充分利用电机的凸极效应来合理分配电流,其中一部分用于产生永磁转矩,另一部分用于产生电磁转矩,达到小电流,大转矩的效果。
值得注意以下两点
- MTPA的推导基于精确的电机模型,但实际情况下电机模型参数大多是未知,且容易收到温度等因素的干扰。因此在实际应用该算法时需注意模型参数的敏感性,必要时需结合在线参数辨识等技术。
- 在实际应用中,为了减小微控制器的运算负担,式(8)(9)并不会在线计算。而是通过提前离线计算并制表,在线查表的方式来得到dq轴电流设定。



)





)


)



(python))


