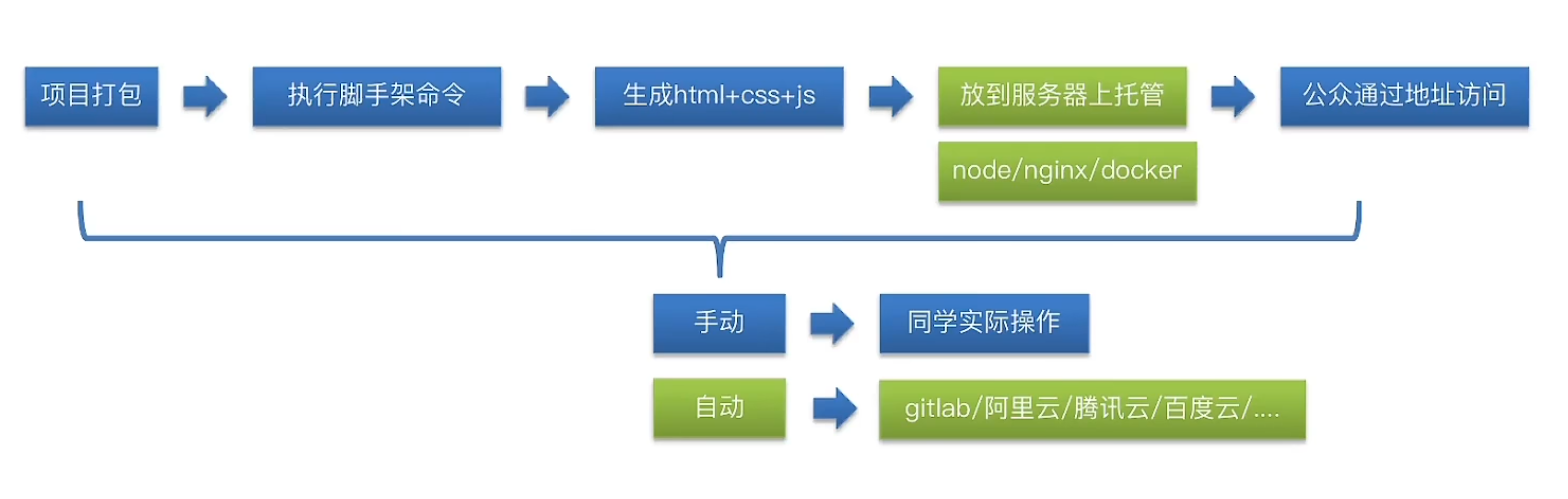
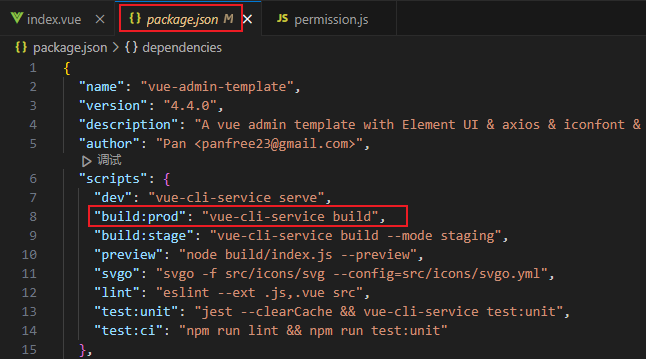
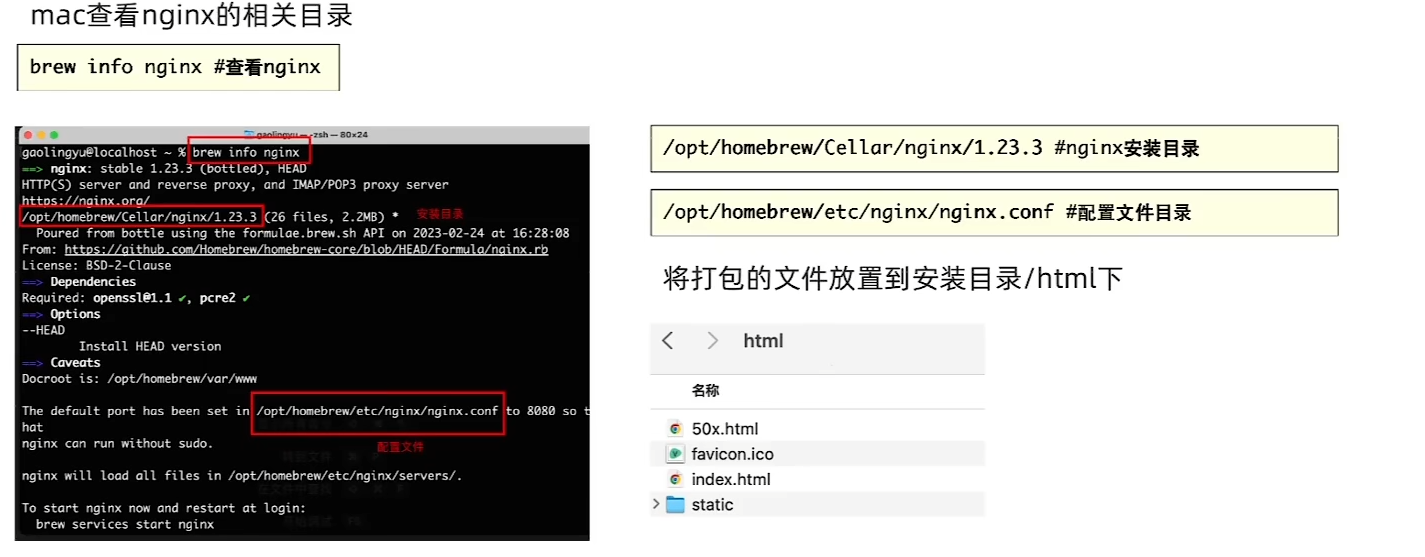
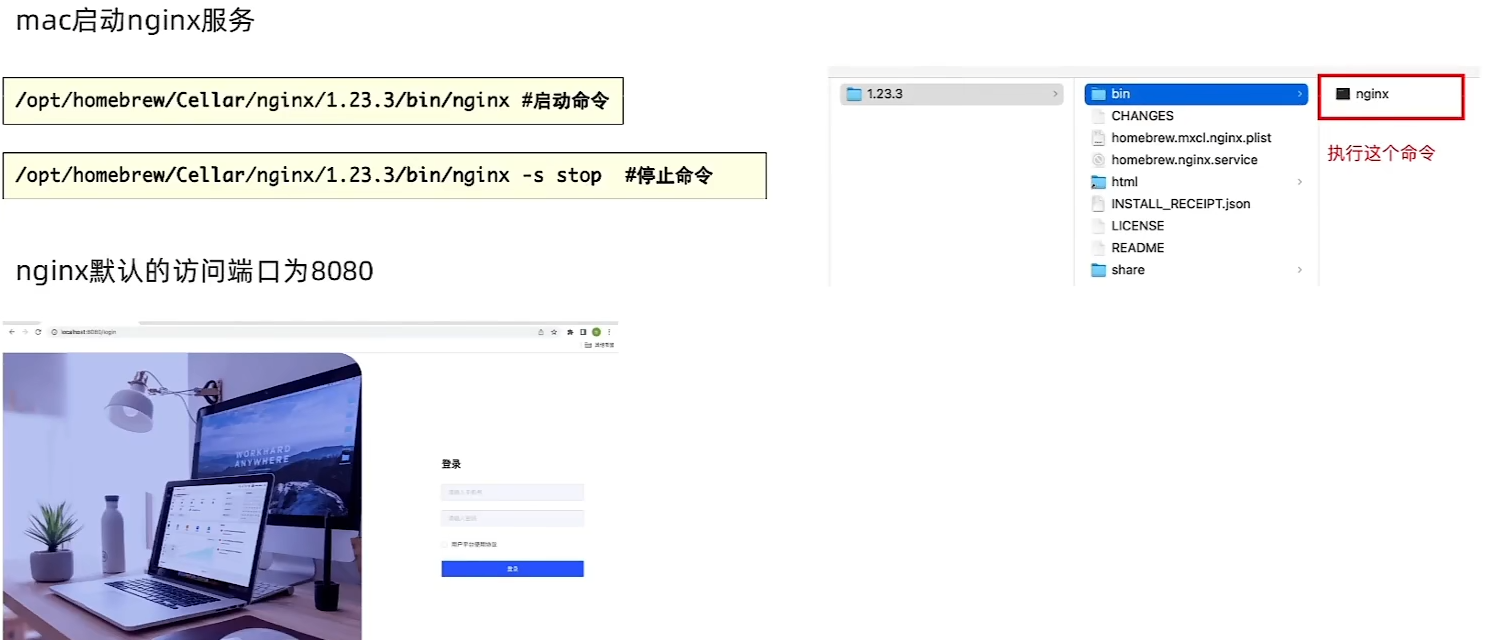
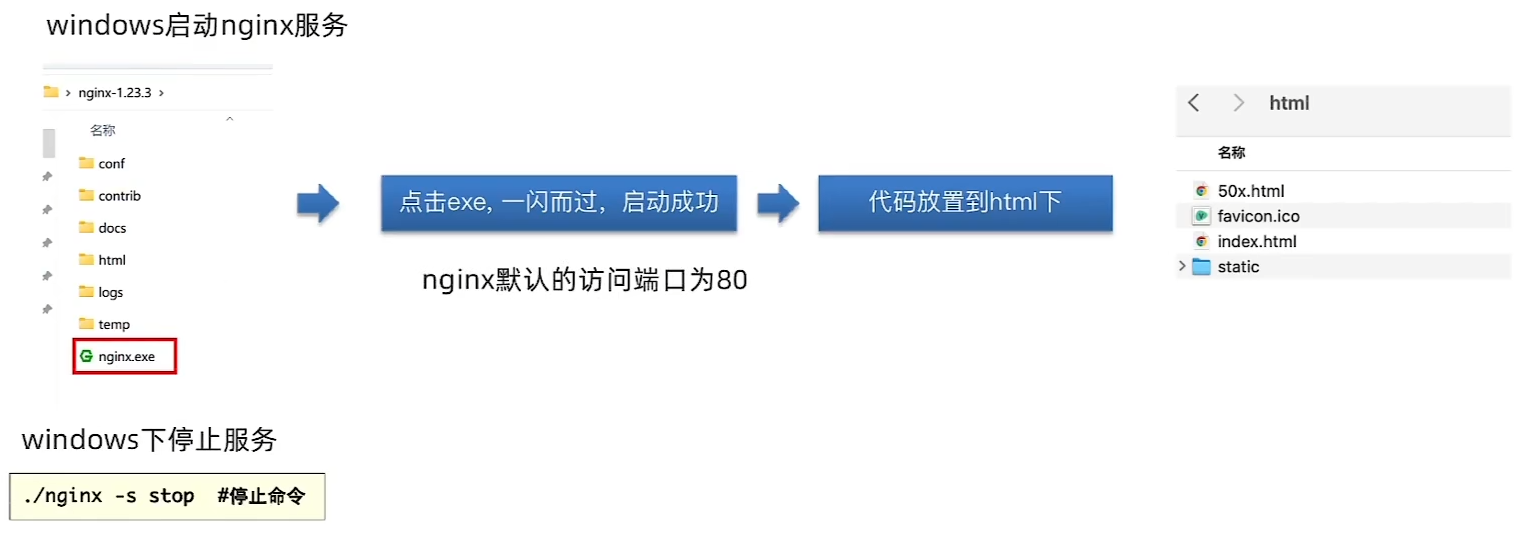
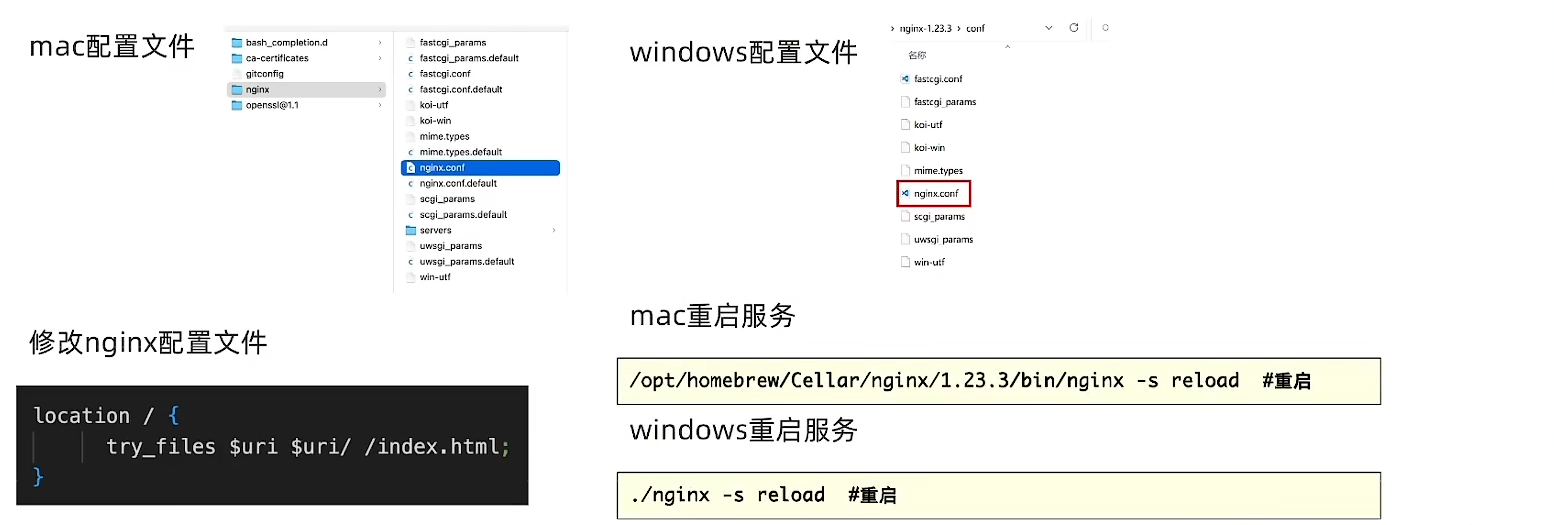
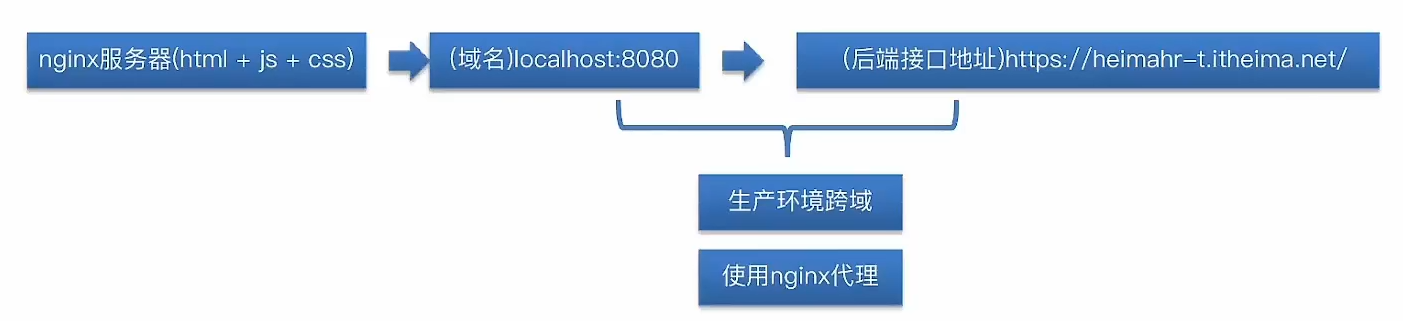
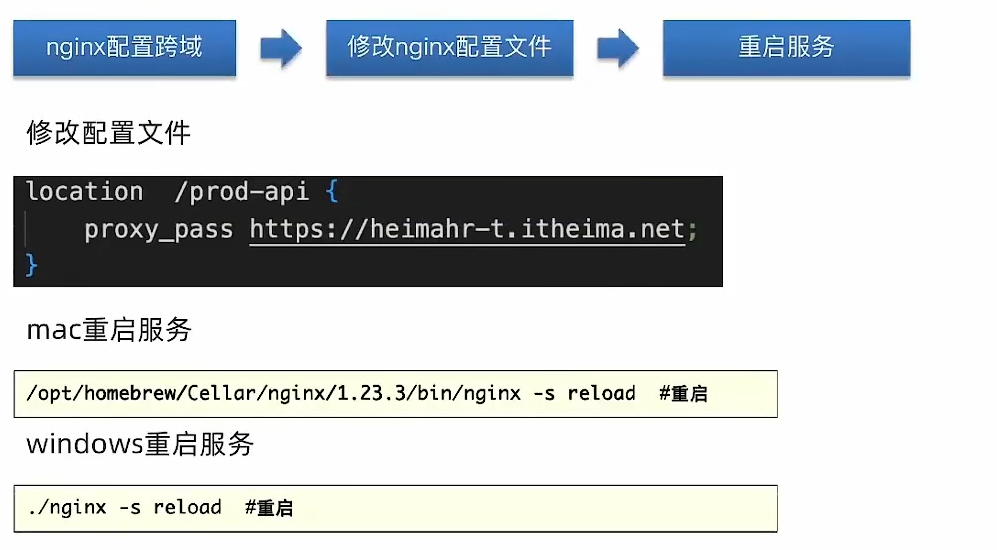
nginx部署上线
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/824582.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
极速、易用、高度定制化的开源社区交流平台:Flarum
Flarum:轻盈高效,引领未来社区互动新风尚的革命性论坛平台- 精选真开源,释放新价值。 概览
Flarum是一款精心打造的现代网站讨论平台,以其精炼高效而著称。作为 esoTalk 和 FluxBB 的理念和技术的集大成者,Flarum 致力…
Ubuntu 20.04 LTS 在3588安卓主板上测试yolov8-1.0版本的yolov8n-seg模型
0. 创建虚拟环境
#!< 创建虚拟环境yolov8
$ sudo pip install virtualenv
$ sudo pip install virtualenvwrapper
$ mkvirtualenv yolov8 -p /usr/bin/python3.81. 将yolov8n-seg.pt转换为yolov8n-seg.onnx文件
#!< 创建项目目录yolov8-rknn并下载yolov8n-seg.pt模型文…
Asp.Net Core中的进程内托管与进程外托管模型
在ASP.NET Core中,托管模型决定了应用程序如何运行及其与Web服务器交互的方式。主要有两种托管模式:进程内托管(In-Process Hosting)和进程外托管(Out-of-Process Hosting)。每种模式都有自己的优势和使用场…
FlinkSQL State的生命周期
FlinkSQL未显示配置state生命周期
FlinkSQL默认没有配置state 的过期时间。也就是说默认情况是FlinkSQL从不清除状态。如果状态后端保存在rocksdb中,直到本地磁盘被打满,服务挂掉,报错如下:
java.io.IOException: [bf3ba881614e…
Python中的异步编程如何工作? —— 理解asyncio库和异步IO的原理
在Python中,异步编程是通过asyncio库和异步IO实现的。异步编程的目的是可以同时执行多个任务,而不需要等待任务完成。
asyncio库是Python 3.4版本引入的标准库,提供了一种基于协程的异步编程模型。协程是一种可以暂停和恢复执行的函数&#…
虚拟机vm桥接模式linux(centos,ubuntu)联网
台式机网线 查看宿主机网络 编辑虚拟机—>虚拟网络编辑器–>更改设置 选择,确定 进入linux系统 输入ip addr找到自己的网卡 我的是eno16777736
centos: 编辑
HWADDR"00:0C:29:54:CE:B8"
TYPE"Ethernet"
BOOTPROTO"…
公网IP多少钱可以购买?
公网IP是指可以在全球范围内访问和识别的唯一IP地址。对于许多企业和个人用户来说,公网IP是实现远程访问、搭建服务器、建立安全连接等重要需求的基础。公网IP的获取并不是免费的,并且价格因供应商和地区而异。 现有公网IP市场
当前,市场上有…
对 Seata 的理解
在微服务架构下,由于数据库和应用服务的拆分,导致原本一个事务单元中的多个DML操作,变成了跨进程或者跨数据库的多个事务单元的多个 DML 操作,而传统的数据库事务无法解决这类的问题,所以就引出了分布式事务的概念。 …
Linux命令-dstat命令(通用的系统资源统计工具)
说明
dstat命令 是一个用来替换vmstat、iostat、netstat、nfsstat和ifstat这些命令的工具,是一个全能系统信息统计工具。与sysstat相比,dstat拥有一个彩色的界面,在手动观察性能状况时,数据比较显眼容易观察;而且dsta…
Pytorch:张量的形状操作
文章目录 一、维度改变1.flatten展开a.函数的基本用法b.示例 2.unsqueeze增维a.函数的基本用法b.示例 3.squeeze降维a.函数的基本用法b.示例 二、张量变形1.view()a.函数的基本用法b.参数:c.注意事项d.示例 2.reshape()a.注意事项b.示例 3.reshape_as()a.函数的基本…
深入理解 pytest Fixture 方法及其应用
当涉及到编写自动化测试时,测试框架和工具的选择对于测试用例的设计和执行非常重要。在Python 中,pytest是一种广泛使用的测试框架,它提供了丰富的功能和灵活的扩展性。其中一个很有用的功 能是fixture方法,它允许我们初始化测试环…
css中backface-visibility使用
backface-visibility 是一个 CSS 属性,用于控制元素的背面是否可见。它主要用于在进行3D转换时控制元素的背面可见性。当一个元素被旋转或进行其他3D变换时,通常浏览器默认会进行背面剪裁(backface culling),使得元素的…
DAY29| 491.递增子序列 ,46.全排列 ,47.全排列II
文章目录 491.递增子序列46.全排列47.全排列II 491.递增子序列 文字讲解:递增子序列 视频讲解:递增子序列 **状态:这题看了文字讲解才AC,掌握了如何在回溯里通过Set集合来对同层节点去重 思路:
代码:
cla…
HTML5漫画风格个人介绍源码
源码介绍
HTML5漫画风格个人介绍源码,源码由HTMLCSSJS组成,记事本打开源码文件可以进行内容文字之类的修改,双击html文件可以本地运行效果,也可以上传到服务器里面,重定向这个界面
效果截图 源码下载
HTML5漫画风格…
设计模式———单例模式
单例也就是只能有一个实例,即只创建一个实例对象,不能有多个。
可能会疑惑,那我写代码的时候注意点,只new一次不就得了。理论上是可以的,但在实际中很难实现,因为你无法预料到后面是否会脑抽一下~~因此我们…
「Python大数据」数据采集-某东产品数据评论获取
前言
本文主要介绍通过python实现数据采集、脚本开发、办公自动化。数据内容范围:星级评分是1-3分、获取数据页面是前50页。
友情提示 法律分析:下列三种情况,爬虫有可能违法,严重的甚至构成犯罪: 爬虫程序规避网站经营者设置的反爬虫措施或者破解服务器防抓取措施,非法…
arm 作业 24/4/17
1、主机向从机发送多个字节的数据
主机发送起始信号
主机发送8bit从机地址1bit写标志(0)
从机回应应答信号
主机发送8bit从机的寄存器地址
从机回应应答信号
主机发送8bit数据
从机回应应答
主机发送8bit数据
从机回应应答
…………
主机发起…
【Pytorch】Conv1d
conv1d 先看看官方文档 再来个简单的例子
import torch
import numpy as np
import torch.nn as nndata np.arange(1, 13).reshape([1, 4, 3])
data torch.tensor(data, dtypetorch.float)
print("[data]:\n", data)
conv nn.Conv1d(in_channels4, out_channels1…
二叉树前序遍历到底部为何会返回到顶部?函数调用栈
前序遍历是一种二叉树的遍历方式,其遍历顺序是先访问根节点,然后递归地遍历左子树,最后递归地遍历右子树。具体来说,前序遍历的顺序是根节点->左子树->右子树。
前序遍历到底部为何会返回到顶部是因为在进行递归遍历时&…









联网)



)









