目录
简述
二次误差函数
交叉熵误差函数
计算剩余节点增量
政安晨的个人主页:政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: 政安晨的机器学习笔记
希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正!
简述
为神经网络中的每个节点(神经元)计算一个常数值。我们将从输出节点开始,然后逐步通过神经网络反向传播。“反向传播”一词就来自这个过程。我们最初计算输出神经元的误差,然后通过神经网络向后传播这些误差。节点增量是我们将为每个节点计算的值。层增量也描述了该值,因为我们可以一次计算一层的增量。在计算输出节点或内部节点时,确定节点增量的方法可能会有所不同。首先计算输出节点,并考虑神经网络的误差函数。
在深度学习的反向传播网络中,计算输出节点增量(即输出误差)和计算剩余节点增量使用的是反向传播算法。
该算法首先计算输出节点增量。输出节点的增量是通过将网络的实际输出与期望输出之间的误差传播回网络中来计算的。具体来说,通过使用损失函数(如均方差误差函数)来计算网络的误差,然后将这个误差从输出层传播回隐藏层。根据链式法则,输出节点增量可以通过乘以导数(激活函数的导数)和误差传播的方式计算出来。
接下来,使用输出节点的增量来计算剩余节点的增量。剩余节点的增量是通过将输出节点的增量传播回隐藏层来计算的。具体来说,根据链式法则,剩余节点的增量可以通过将输出节点的增量乘以权重矩阵的转置并乘以隐藏层节点的导数来计算。
通过反向传播算法,可以计算出网络中所有节点的增量,从而根据这些增量来更新网络的权重和偏差,进一步优化网络的性能。
二次误差函数
神经网络的程序员经常使用二次误差函数。实际上,你可以在网络上找到许多使用二次误差函数的示例。如果你正在阅读一个示例程序,但未提及具体的误差函数,那么该程序可能使用了二次误差函数,也称为MSE函数,我们在前文“训练和评估”中讨论过。
下面公式展示了MSE函数:
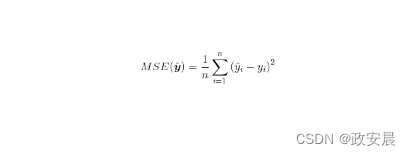
下面公式将神经网络的实际输出(y)与预期输出(y^)进行了比较。变量n为训练元素的数量乘以输出神经元的数量。MSE将多个输出神经元处理为单个输出神经元的情况。
下面公式展示了使用二次误差函数的节点增量:
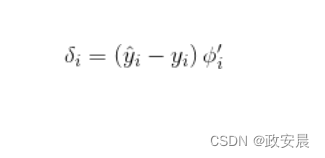
二次误差函数非常简单,因为它取了神经网络的预期输出与实际输出之间的差。′表示激活函数的导数。
交叉熵误差函数
二次误差函数有时可能需要很长时间才能正确调整权重。下面公式展示了交叉熵误差(Cross-entropy Error,CE)函数:
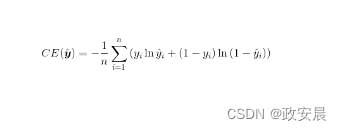
如下面公式所示,采用交叉熵误差函数的节点增量计算要比采用MSE函数简单得多。
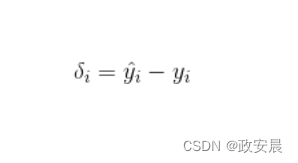
交叉熵误差函数通常会比二次误差函数结果更好,因为二次误差函数会为误差创建一个陡峭的梯度。我们推荐采用交叉熵误差函数。
计算剩余节点增量
既然已经根据适当的误差函数计算了输出节点的增量,我们就可以计算内部节点的增量,如下公式所示:
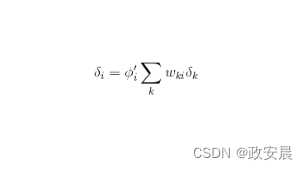
我们将为所有隐藏和无偏置神经元计算节点增量,但无须为输入和偏置神经元计算节点增量。即使我们可以使用上面公式轻松计算输入和偏置神经元的节点增量,梯度计算也不需要这些值。你很快会看到,权重的梯度计算仅考虑权重所连接的神经元。偏置和输入神经元只是连接的起点,它们从来不是终点。






考试速通经验分享(含答案))


:系统基本架构讨论)





)
【计算机基础三】)



