目录

一，二叉树的链式结构

二，二叉链的接口实现

        1，二叉链的创建

        2，接口函数

        3，动态创立新结点

        4，创建二叉树

        5，前序遍历

        6，中序遍历

        7，后序遍历

三，结点个数以及高度等

        1，接口函数

        2，结点个数

        3，叶子结点个数

        4，二叉树高度

        5，二叉树第k层结点个数

        6，二叉树查找值为x的结点

---

一，二叉树的链式结构

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系；

通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。

链式结构又分为二叉链和三叉链，这里我们学习二叉链；

 二叉树是：

1，空树

2，非空：根节点，根节点的左子树、根节点的右子树组成的。

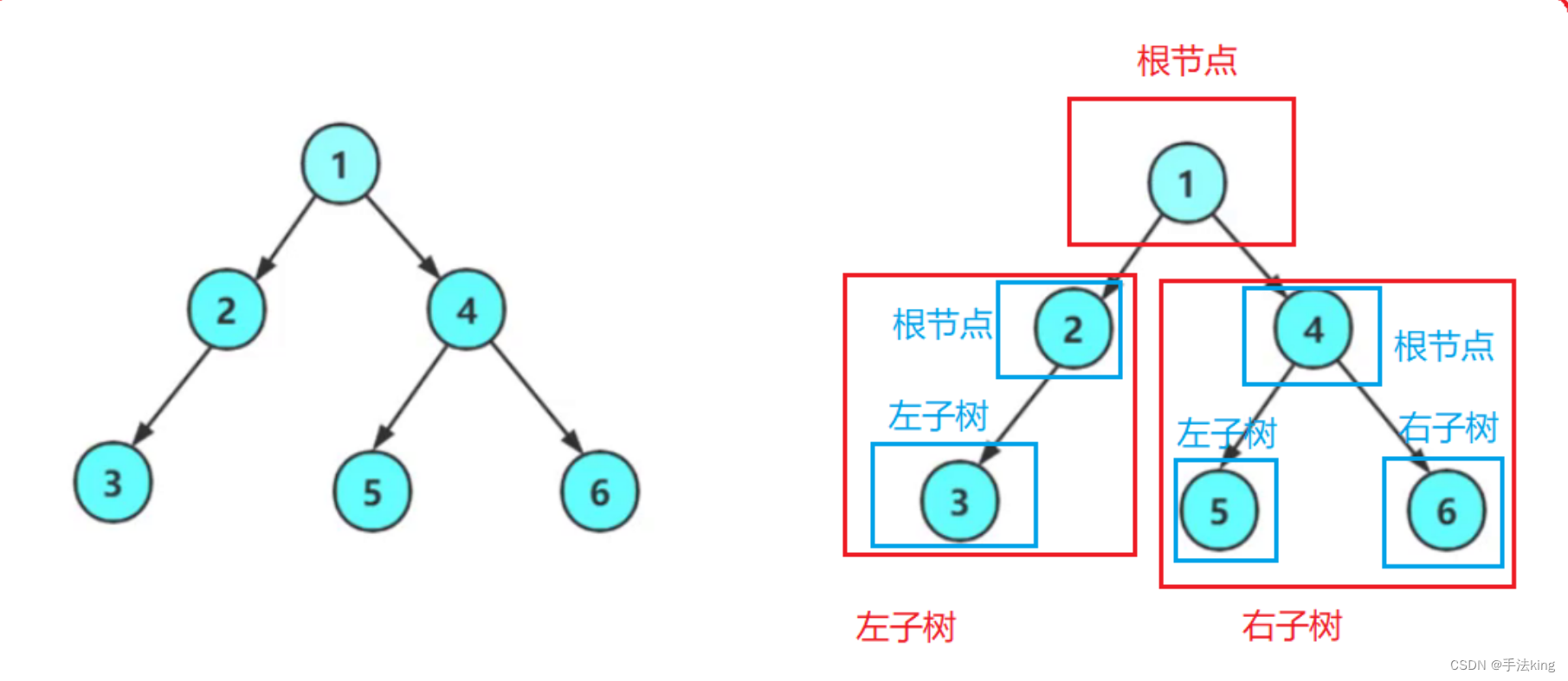
从图示中可以看出，二叉树定义是递归式的也称递归树，因此后序基本操作中基本都是按照该概念实现的；

 二叉链结构图示；

二，二叉链的接口实现

        1，二叉链的创建

typedef int BTDataType;
//二叉链
typedef struct BinaryTreeNode
{BTDataType data; // 当前结点值域	struct BinaryTreeNode* left; // 指向当前结点左孩子struct BinaryTreeNode* right; // 指向当前结点右孩子
}BTNode;

首先创建一个结构体表示二叉链，data是当前结点的值域，BTDataType是储存的值的数据类型；

left是指向当前结点左孩子，right是指向当前结点右孩子；

这里的BTDataType是int的重命名，也可以说是数据类型的重命名，这样统一化方便后续更改；

        2，接口函数

//动态创立新结点
BTNode* BuyNode(BTDataType x);
//创建二叉树
BTNode* GreatBTree();
//前序遍历
void PrevOrder(BTNode* root);
//中序遍历
void InOrder(BTNode* root);
//后序遍历
void PostOrder(BTNode* root);

这是以上要实现的接口函数；

        3，动态创立新结点

//动态创立新结点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}

后面创立新结点时直接调用此函数，一定要向堆区申请空间，这样函数结束空间会保留不会被回收；

将data赋新值，left与right都指向空，再返回结点指针即可；

        4，创建二叉树

//创建二叉树
BTNode* GreatBTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

然后我们申请结点来构造二叉树，通过链接将新结点链接起来；

创建的二叉树结构图示如下：

        5，前序遍历

//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

二叉树的前序，中序，后续遍历都是同一种思路：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——根结点---->左子树--->右子树

2. 中序遍历(Inorder Traversal)——左子树--->根结点--->右子树

3. 后序遍历(Postorder Traversal)——左子树--->右子树--->根结点

这里要用到递归思想：这里NULL用N表示，建议画图来理解，一层一层遍历下去；

前序遍历：

先访问根结点（1）然后访问其左子树（2）；打印 1

此时根结点为（2）然后访问其左子树（3）；打印1 2

此时根结点为（3）然后访问其左子树（NULL）；打印1 2 3

此时根结点为（NULL）return NULL到（3），然后访问（3）的右子树（NULL）；打印1 2 3 N

此时根结点为（NULL）return NULL到（3），此时对（3）也就是对（2）的左子树的访问结束了，然后访问（2）的右子树（NULL)；打印1 2 3 N N

此时根结点为（NULL）return NULL到（2），此时对（2）也就是对（1）的左子树访问结束了，然后访问（1）的右子树（4）；打印1 2 3 N N N

此时根结点为（4）然后访问其左子树（5）；打印1 2 3 N N N 4

此时根结点为（5）然后访问其左子树（NULL）；打印1 2 3 N N N 4 5

此时根结点为（NULL）return NULL到（5）然后访问（5）的右子树（NULL）；打印1 2 3 N N N 4 5 N

此时根结点为（NULL）return NULL到（5）此时对（5）也就是对（4）的左子树的访问结束了，然后访问（4）的右子树（6）；打印 1 2 3 N N N 4 5 N N

此时根结点为（6）然后访问其左子树（NULL）；打印1 2 3 N N N 4 5 N N 6

此时根结点为（NULL）return NULL到（6）然后访问（6）的右子树（NULL）；打印1 2 3 N N N 4 5 N N 6 N

此时根结点为（NULL）return NULL到（6），此时对（6）也就是对（4）的右子树的访问结束了，此时对（4）也就是对（1）的右子树的访问结束了，此时对（1）的访问也结束了，前序遍历也就结束了；打印1 2 3 N N N 4 5 N N 6 N N

图解思路示例：

    

BTNode* root = GreatBTree();
//前序遍历
PrevOrder(root);

这就是前序遍历；

        6，中序遍历

//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}

中序遍历：左子树--->根结点--->右子树

跟前序遍历思路一致，就是换了一下访问的顺序，按照前序遍历的思路来就完事了；

//中序遍历
InOrder(root);
printf("\n");

        7，后序遍历

//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

后序遍历：左子树--->右子树--->根结点

思路还是一致的，就是换了一下访问顺序，前，中，后序遍历的思路都是一致的，只要搞清楚其中一个就全部拿捏了；

//后续遍历
PostOrder(root);
printf("\n");

 这里对二叉链的基础遍历就实现完全了，有人说还有一个层序遍历，这个遍历需要用到队列，目前C语言阶段实现太过于繁琐，后序博主会补上；

三，结点个数以及高度等

像此类问题也都是递归问题，更加看重我们对函数栈帧的理解；

        1，接口函数

//结点个数
int	SumNode(BTNode* root);
//叶子结点个数
int LeafNode(BTNode* root);
//二叉树高度
int HeightTree(BTNode* root);
//二叉树第k层结点个数
int BTreeLeveSize(BTNode* root, int k);
//二叉树查找值为x的结点
BTNode* BTreeFine(BTNode* root, int x);

以上是要实现的函数；

        2，结点个数

//结点个数
int SumNode(BTNode* root)
{return root == NULL ? 0 : SumNode(root->left) + SumNode(root->right) + 1;
}

递归其实说难也难，说不难也不难，是有技巧在里面的；

1，大事化小：根结点为（1）的二叉树的结点总和==>左子树（2）的结点总和加上右子树（4）的结点总和再加上本身的结点个数1，然后根结点为（2）的结点总和==>左子树（3）的总和加上NULL加1，这就是规律；【（1）=（2）+（4）+1 】

2，结束条件，当结点为NULL时返回0；

//结点个数
printf("%d\n", SumNode(root));

        3，叶子结点个数

//叶子结点个数
int LeafNode(BTNode* root)
{if (root == NULL){return 0;}if (root->left==NULL && root->right==NULL){return 1;}else{return LeafNode(root->left) + LeafNode(root->right);}
}

 

大事化小：求根结点为（1）的二叉树的叶子节点的个数==>其左子树（2）加上其右子树（4）的叶子节点的个数；【（1）=（2）+（4）】

结束条件：当结点为NULL时返回0，当结点的左右子树都为NULL时返回1；

        4，二叉树高度

//二叉树高度
int HeightTree(BTNode* root)
{if (root == NULL){return 0;}int left = HeightTree(root->left);int right = HeightTree(root->right);return left > right ? left + 1 : right + 1;
}

大事化小：求根结点为（1）的二叉树的高度==>其左子树（2）与右子树（4）中高的一颗的高度加上本身的高度1；【（1）=（2）>（4）？（2）+1：（4）+1 】

结束条件：当结点为NULL时返回0；

//二叉树高度
printf("%d\n", HeightTree(root));

        5，二叉树第k层结点个数

//二叉树第k层结点个数
int BTreeLeveSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BTreeLeveSize(root->left, k - 1)  + BTreeLeveSize(root->right, k - 1);
}

大事化小：求根结点为（1）的二叉树第K层的结点个数==>其左子树（2）加上右子树（4）中第K-1层结点的个数；【（1）=（2）+（4）】

结束条件：当结点为NULL时返回0，当K等于1时返回1；

//二叉树第k层结点个数
printf("%d\n", BTreeLeveSize(root,3));

        6，二叉树查找值为x的结点

//二叉树查找值为x的结点
BTNode* BTreeFine(BTNode* root, int x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}if (BTreeFine(root->left, x) == NULL){return BTreeFine(root->right, x);}else{return BTreeFine(root->left, x);}
}

大事化小：查找根结点为（1）的二叉树中值为x的结点==>查找其左子树（2）与右子树（4）中值为x的结点；

结束条件：当结点为NULL时返回NULL，当结点的值为x时返回该结点；

思路：所以当其中一个子树不为NULL时就是所求的结点，如果左子树不为空则返回左子树的结点，否则返回右子树的结点，如果左右都为空那也返回右子树的结点；

//二叉树查找值为x的结点
BTNode* ret = BTreeFine(root, 6);
printf("%d\n", ret->data);ret = BTreeFine(root, 3);
printf("%d\n", ret->data);

到这里就结束了，通过这些题目也充分的认识了二叉树（递归树），这就是递归算法，还是要多画图来理解，递归基层的知识就是函数栈帧的创建与销毁；

第三阶段就到这里了，这阶段带大家了解一下二叉树（递归树）的递归思想；

后面博主会陆续更新；

如有不足之处欢迎来补充交流！

完结。。

---